Tout le monde peut apprendre les mathématiques, que ce soit en mathématiques ou à l'école. Après avoir discuté des manières d'être un bon étudiant en mathématiques, cet article vous apprendra la progression de base des cours de mathématiques et vous donnera les éléments de base que vous devrez apprendre dans chaque cours. Ensuite, l'article passera en revue les bases de l'apprentissage de l'arithmétique, ce qui aidera les enfants du primaire et ceux qui ont besoin de se familiariser avec les principes fondamentaux.
Première partie de six:
Clés pour être un bon étudiant en mathématiques
-
 1 Présentez-vous en classe. Lorsque vous manquez le cours, vous devez apprendre les concepts d'un camarade de classe ou de votre manuel. Vous n'obtiendrez jamais un aussi bon aperçu de vos amis ou du texte que vous le ferez de votre professeur.
1 Présentez-vous en classe. Lorsque vous manquez le cours, vous devez apprendre les concepts d'un camarade de classe ou de votre manuel. Vous n'obtiendrez jamais un aussi bon aperçu de vos amis ou du texte que vous le ferez de votre professeur. - Viens en classe à l'heure. En fait, venez un peu plus tôt et ouvrez votre cahier au bon endroit, ouvrez votre manuel et sortez votre calculatrice pour que vous soyez prêt à commencer lorsque votre professeur est prêt à démarrer.
- Ne sautez que les cours si vous êtes malade. Lorsque vous manquez le cours, parlez-en à un camarade de classe pour savoir de quoi le professeur a parlé et quels devoirs ont été assignés.
-
 2 Travaillez avec votre professeur. Si votre professeur a des problèmes à l’avant de votre classe, travaillez avec votre professeur dans votre cahier.
2 Travaillez avec votre professeur. Si votre professeur a des problèmes à l’avant de votre classe, travaillez avec votre professeur dans votre cahier. - Assurez-vous que vos notes sont claires et faciles à lire. Ne vous contentez pas de noter les problèmes. Notez également tout ce que l'enseignant dit pour améliorer votre compréhension des concepts.
- Travaillez tous les exemples de problèmes que votre professeur publie pour vous. Lorsque l'enseignant se promène dans la classe pendant que vous travaillez, répondez aux questions.
- Participez pendant que l'enseignant travaille un problème. N'attendez pas que votre professeur vous appelle. Faites du bénévolat pour répondre lorsque vous connaissez la réponse et levez la main pour poser des questions lorsque vous n'êtes pas certain de ce qui est enseigné.
-
 3 Faites vos devoirs le jour même où il est assigné. Lorsque vous faites les devoirs le même jour, les concepts sont frais dans votre esprit. Parfois, terminer vos devoirs le même jour n'est pas possible. Assurez-vous que vos devoirs sont complets avant de vous rendre en classe.
3 Faites vos devoirs le jour même où il est assigné. Lorsque vous faites les devoirs le même jour, les concepts sont frais dans votre esprit. Parfois, terminer vos devoirs le même jour n'est pas possible. Assurez-vous que vos devoirs sont complets avant de vous rendre en classe. -
 4 Faites un effort en dehors des cours si vous avez besoin d'aide. Rendez-vous chez votre professeur pendant sa période libre ou pendant les heures de bureau.
4 Faites un effort en dehors des cours si vous avez besoin d'aide. Rendez-vous chez votre professeur pendant sa période libre ou pendant les heures de bureau. - Si vous avez un centre de mathématiques à votre école, découvrez les heures d'ouverture et obtenez de l'aide.
- Rejoignez un groupe d'étude. Les bons groupes d'étude contiennent généralement 4 ou 5 personnes dans un bon mélange de niveaux d'aptitude. Si vous êtes un étudiant en "C" en mathématiques, alors rejoignez un groupe qui a 2 ou 3 étudiants "A" ou "B" afin que vous puissiez élever votre niveau. Évitez de rejoindre un groupe d'étudiants dont les notes sont inférieures aux vôtres.[1]
Deuxième partie de six:
Apprendre les mathématiques à l'école
-
 1 Commencez par l'arithmétique. Dans la plupart des écoles, les élèves travaillent sur l'arithmétique pendant les classes élémentaires. L'arithmétique comprend les principes fondamentaux de l'addition, de la soustraction, de la multiplication et de la division.
1 Commencez par l'arithmétique. Dans la plupart des écoles, les élèves travaillent sur l'arithmétique pendant les classes élémentaires. L'arithmétique comprend les principes fondamentaux de l'addition, de la soustraction, de la multiplication et de la division. - Travailler sur des exercices. Faire de nombreux problèmes arithmétiques, encore et encore, est le meilleur moyen d’abattre les principes fondamentaux. Recherchez les logiciels qui vous permettront de résoudre de nombreux problèmes mathématiques. Recherchez également des exercices chronométrés pour augmenter votre vitesse.
- La répétition est la base des mathématiques. Le concept doit être non seulement appris, mais mis au travail pour que vous vous en souveniez!
- Vous pouvez également trouver des exercices d'arithmétique en ligne et télécharger des applications arithmétiques sur votre appareil mobile.
-
 2 Progrès en pré-algèbre. Ce cours fournira les éléments de base dont vous aurez besoin pour résoudre les problèmes d'algèbre ultérieurement.
2 Progrès en pré-algèbre. Ce cours fournira les éléments de base dont vous aurez besoin pour résoudre les problèmes d'algèbre ultérieurement. - En savoir plus sur les fractions et les décimales. Vous apprendrez à ajouter, soustraire, multiplier et diviser les fractions et les décimales. En ce qui concerne les fractions, vous apprendrez à réduire les fractions et à interpréter les nombres mélangés. En ce qui concerne les décimales, vous comprendrez la valeur de la position et vous pourrez utiliser des décimales dans les problèmes de mots.
- Ratios d'étude, proportions et pourcentages. Ces concepts vous aideront à apprendre à faire des comparaisons.
- Résoudre des carrés et des racines carrées. Lorsque vous maîtriserez ce sujet, vous aurez des carrés parfaits de nombreux nombres mémorisés. Vous pourrez également travailler avec des équations contenant des racines carrées.
- Présentez-vous à la géométrie de base. Vous apprendrez toutes les formes ainsi que les concepts 3D. Vous apprendrez également des concepts tels que la surface, le périmètre, le volume et la surface, ainsi que des informations sur les lignes et les angles parallèles et perpendiculaires.
- Comprendre certaines statistiques de base. En pré-algèbre, votre introduction aux statistiques comprend principalement des éléments graphiques tels que des graphiques, des diagrammes de dispersion, des tracés de feuilles et de tiges et des histogrammes.
- Apprenez les bases de l'algèbre. Celles-ci incluront des concepts tels que la résolution d'équations simples contenant des variables, l'apprentissage de propriétés comme la propriété distributive, la représentation graphique d'équations simples et la résolution des inégalités.
-
 3 Avance à l'Algèbre I. Au cours de votre première année d’algèbre, vous apprendrez les symboles de base de l’algèbre. Vous apprendrez également à:
3 Avance à l'Algèbre I. Au cours de votre première année d’algèbre, vous apprendrez les symboles de base de l’algèbre. Vous apprendrez également à: - Résoudre des équations linéaires et des inégalités qui contiennent 1 à 2 variables. Vous apprendrez à résoudre ces problèmes non seulement sur papier, mais aussi sur une calculatrice.
- S'attaquer aux problèmes de mots. Vous serez surpris de voir combien de problèmes quotidiens que vous rencontrerez dans votre avenir impliquent la capacité de résoudre des problèmes de mots algébriques. Par exemple, vous utiliserez l'algèbre pour déterminer le taux d'intérêt que vous gagnez sur votre compte bancaire ou sur vos investissements. Vous pouvez également utiliser l'algèbre pour déterminer combien de temps vous devrez parcourir en fonction de la vitesse de votre voiture.
- Travailler avec des exposants. Lorsque vous commencez à résoudre des équations avec des polynômes (expressions contenant à la fois des nombres et des variables), vous devez comprendre comment utiliser les exposants. Cela peut également inclure le travail avec la notation scientifique.Une fois que vous avez des exposants, vous pouvez apprendre à ajouter, soustraire, multiplier et diviser des expressions polynomiales.
- Comprendre les fonctions et les graphiques. En algèbre, vous allez vraiment entrer dans les équations graphiques. Vous apprendrez à calculer la pente d'une ligne, à mettre les équations en forme de pente et à calculer les interceptions x et y d'une ligne à l'aide d'une forme d'interception de pente.
- Déterminer des systèmes d'équations. Parfois, vous obtenez 2 équations séparées avec des variables x et y, et vous devez résoudre x ou y pour les deux équations. Heureusement, vous apprendrez de nombreuses astuces pour résoudre ces équations, notamment la représentation graphique, la substitution et l'ajout.[2]
-
 4 Entrez dans la géométrie. En géométrie, vous apprendrez les propriétés des lignes, des segments, des angles et des formes.[3]
4 Entrez dans la géométrie. En géométrie, vous apprendrez les propriétés des lignes, des segments, des angles et des formes.[3] - Vous mémoriserez un certain nombre de théorèmes et de corollaires qui vous aideront à comprendre les règles de la géométrie.
- Vous apprendrez à calculer l'aire d'un cercle, à utiliser le théorème de Pythagore et à déterminer les relations entre les angles et les côtés des triangles spéciaux.
- Vous verrez beaucoup de géométrie sur les futurs tests standardisés tels que le SAT, le ACT et le GRE.
-
 5 Prenez Algèbre II. Algèbre II s'appuie sur les concepts que vous avez appris en Algèbre I mais ajoute des sujets plus complexes impliquant des fonctions et des matrices non linéaires plus complexes.
5 Prenez Algèbre II. Algèbre II s'appuie sur les concepts que vous avez appris en Algèbre I mais ajoute des sujets plus complexes impliquant des fonctions et des matrices non linéaires plus complexes. -
 6 S'attaquer à la trigonométrie. Vous connaissez les mots de trig: sinus, cosinus, tangente, etc. La trigonométrie vous apprendra de nombreuses façons pratiques de calculer des angles et des longueurs de lignes.
6 S'attaquer à la trigonométrie. Vous connaissez les mots de trig: sinus, cosinus, tangente, etc. La trigonométrie vous apprendra de nombreuses façons pratiques de calculer des angles et des longueurs de lignes. -
 7 Comptez sur des calculs. Le calcul peut sembler intimidant, mais c'est un outil incroyable pour comprendre à la fois le comportement des nombres et le monde qui vous entoure.
7 Comptez sur des calculs. Le calcul peut sembler intimidant, mais c'est un outil incroyable pour comprendre à la fois le comportement des nombres et le monde qui vous entoure. - Le calcul vous apprendra les fonctions et les limites. Vous verrez le comportement ou un certain nombre de fonctions utiles, y compris les fonctions e ^ x et logarithmiques.
- Vous apprendrez également à calculer et à travailler avec des dérivés. Une première dérivée vous donne des informations basées sur la pente d'une ligne tangente à une équation. Par exemple, un dérivé vous indique le taux auquel quelque chose change dans une situation non linéaire. Une seconde dérivée vous dira si une fonction augmente ou diminue selon un certain intervalle de manière à pouvoir déterminer la concavité d'une fonction.
- Integrals vous apprendra à calculer la surface sous une courbe ainsi que le volume.
- Le calcul au lycée se termine généralement par des séquences et des séries. Bien que les étudiants ne voient pas beaucoup d'applications pour les séries, ils sont importants pour les personnes qui étudient les équations différentielles.
- Le calcul n'est encore que le début pour certains. Si vous envisagez une carrière avec une forte implication en mathématiques et en sciences, comme un ingénieur, essayez d'aller un peu plus loin![4]
Troisième partie de six:
Fondamentaux Mathématiques - Ace Some Addition
-
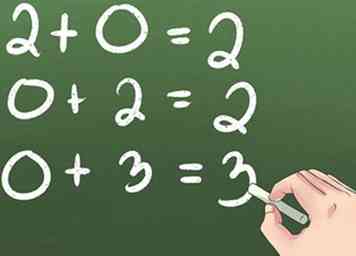 1 Commencez par "+1" faits. L'ajout de 1 à un nombre vous amène au numéro le plus élevé suivant sur la droite numérique. Par exemple, 2 + 1 = 3.
1 Commencez par "+1" faits. L'ajout de 1 à un nombre vous amène au numéro le plus élevé suivant sur la droite numérique. Par exemple, 2 + 1 = 3. -
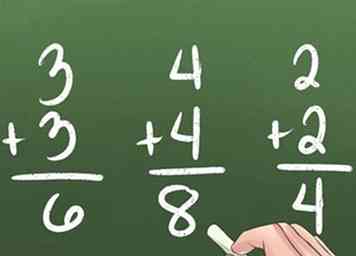 2 Comprendre les zéros. Tout nombre ajouté à zéro est égal au même nombre car "zéro" est identique à "rien".
2 Comprendre les zéros. Tout nombre ajouté à zéro est égal au même nombre car "zéro" est identique à "rien". -
 3 Apprendre double Les doublons sont des problèmes qui impliquent l'ajout de deux numéros identiques. Par exemple, 3 + 3 = 6 est un exemple d'équation impliquant des doubles.
3 Apprendre double Les doublons sont des problèmes qui impliquent l'ajout de deux numéros identiques. Par exemple, 3 + 3 = 6 est un exemple d'équation impliquant des doubles. -
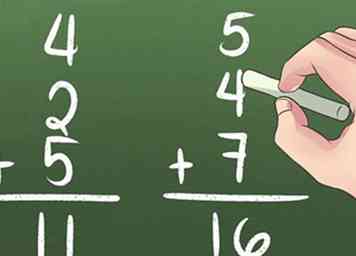 4 Utilisez le mappage pour en savoir plus sur les autres solutions d’ajout. Dans l'exemple ci-dessous, vous apprendrez en mappant ce qui se passe lorsque vous ajoutez 3 à 5, 2 et 1. Essayez les problèmes "ajouter 2" par vous-même.
4 Utilisez le mappage pour en savoir plus sur les autres solutions d’ajout. Dans l'exemple ci-dessous, vous apprendrez en mappant ce qui se passe lorsque vous ajoutez 3 à 5, 2 et 1. Essayez les problèmes "ajouter 2" par vous-même. -
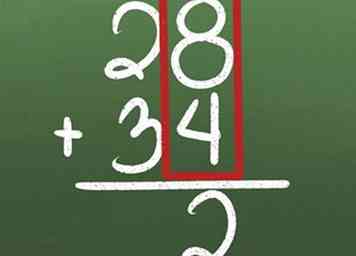 5 Aller au-delà de 10. Apprenez à ajouter 3 nombres ensemble pour obtenir un nombre supérieur à 10.
5 Aller au-delà de 10. Apprenez à ajouter 3 nombres ensemble pour obtenir un nombre supérieur à 10. -
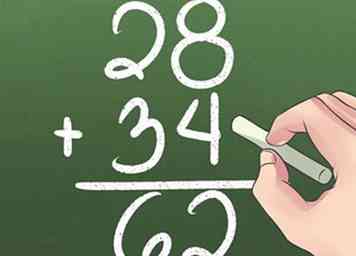 6 Ajouter des nombres plus importants. Apprenez à regrouper les 1 dans les 10 places, les 10 dans les 100, etc.
6 Ajouter des nombres plus importants. Apprenez à regrouper les 1 dans les 10 places, les 10 dans les 100, etc. - Ajoutez les numéros dans la colonne de droite en premier. 8 + 4 = 12, ce qui signifie que vous avez 1 10 et 2 1. Notez les 2 sous la colonne 1s.
- Écrivez le 1 sur la colonne 10s.
- Ajouter la colonne 10s ensemble.
Partie quatre de six:
Fondements mathématiques - Stratégies de soustraction
-
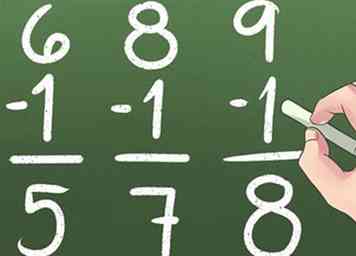 1 Commencez par "en arrière 1."En soustrayant 1 à un nombre, vous retournez à 1 nombre. Par exemple, 4 - 1 = 3.
1 Commencez par "en arrière 1."En soustrayant 1 à un nombre, vous retournez à 1 nombre. Par exemple, 4 - 1 = 3. -
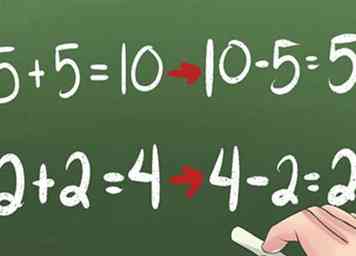 2 Apprendre en double soustraction. Par exemple, vous ajoutez les doubles 5 + 5 pour obtenir 10. Écrivez simplement l'équation en arrière pour obtenir 10 - 5 = 5.
2 Apprendre en double soustraction. Par exemple, vous ajoutez les doubles 5 + 5 pour obtenir 10. Écrivez simplement l'équation en arrière pour obtenir 10 - 5 = 5. - Si 5 + 5 = 10, alors 10 - 5 = 5.
- Si 2 + 2 = 4, alors 4 - 2 = 2.
-
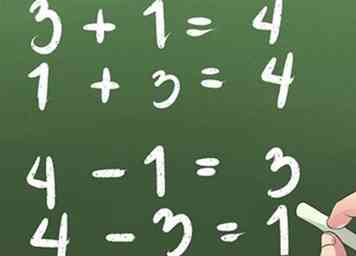 3 Mémoriser les familles de faits. Par exemple:
3 Mémoriser les familles de faits. Par exemple: - 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1
-
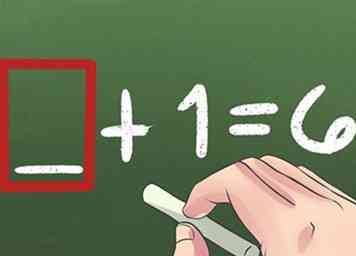 4 Trouvez les numéros manquants. Par exemple, ___ + 1 = 6 (la réponse est 5). Cela pose également les bases de l'algèbre et au-delà.
4 Trouvez les numéros manquants. Par exemple, ___ + 1 = 6 (la réponse est 5). Cela pose également les bases de l'algèbre et au-delà. -
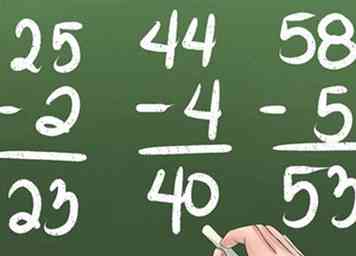 5 Mémoriser les faits de soustraction jusqu'à 20.
5 Mémoriser les faits de soustraction jusqu'à 20. -
 6 Entraînez-vous à soustraire les nombres à un chiffre des nombres à deux chiffres sans emprunter. Soustrayez les nombres dans la colonne 1 et ramenez le nombre dans la colonne 10s.
6 Entraînez-vous à soustraire les nombres à un chiffre des nombres à deux chiffres sans emprunter. Soustrayez les nombres dans la colonne 1 et ramenez le nombre dans la colonne 10s. -
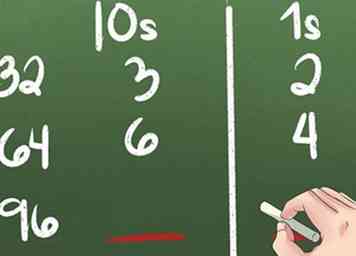 7 Pratiquez la valeur du lieu pour vous préparer à la soustraction avec l'emprunt.
7 Pratiquez la valeur du lieu pour vous préparer à la soustraction avec l'emprunt. - 32 = 3 10 et 2 1.
- 64 = 6 10 et 4 1.
- 96 = __ 10s et __ 1s.
-
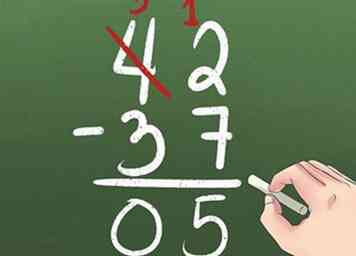 8 Soustraire à l'emprunt.
8 Soustraire à l'emprunt. - Vous voulez soustraire 42 - 37. Vous commencez par essayer de soustraire 2 - 7 dans la colonne 1s. Cependant, ça ne marche pas!
- Empruntez 10 de la colonne 10s et placez-la dans la colonne 1s. Au lieu de 4 10, vous avez maintenant 3 10. Au lieu de 2 1, vous avez maintenant 12 1.
- Soustrayez votre première colonne: 12 - 7 = 5. Vérifiez ensuite la colonne 10s. Puisque 3 - 3 = 0, vous n'avez pas à écrire 0. Votre réponse est 5.[5]
Cinquième partie de six:
Fondamentaux Mathématiques - Multiplication Maître
-
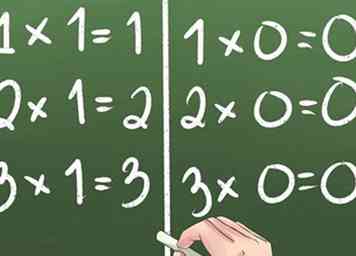 1 Commencez avec 1 et 0. Tout nombre de fois 1 est égal à lui-même. Tout nombre de fois zéro est égal à zéro.
1 Commencez avec 1 et 0. Tout nombre de fois 1 est égal à lui-même. Tout nombre de fois zéro est égal à zéro. -
 2 Mémorisez la table de multiplication.
2 Mémorisez la table de multiplication. -
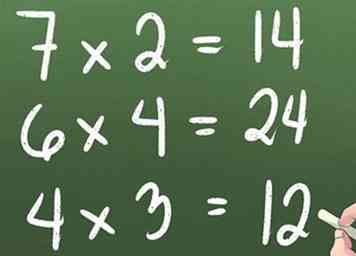 3Pratiquez les problèmes de multiplication à un chiffre
3Pratiquez les problèmes de multiplication à un chiffre -
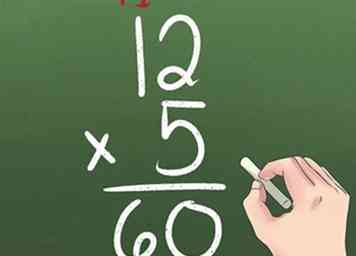 4 Multipliez les nombres à 2 chiffres par les nombres à 1 chiffre.
4 Multipliez les nombres à 2 chiffres par les nombres à 1 chiffre. - Multipliez le nombre en bas à droite par le numéro en haut à droite.
- Multipliez le nombre en bas à droite par le numéro en haut à gauche.
-
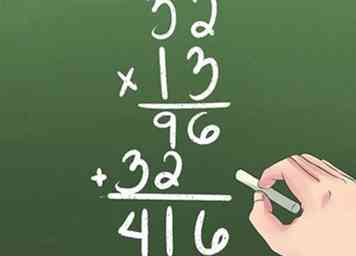 5 Multipliez 2 nombres à 2 chiffres.
5 Multipliez 2 nombres à 2 chiffres. - Multipliez le nombre en bas à droite par les chiffres en haut à droite et ensuite en haut à gauche.
- Déplacez la deuxième rangée d'un chiffre vers la gauche.
- Multipliez le nombre en bas à gauche par les chiffres en haut à droite puis les chiffres en haut à gauche.
- Ajoutez les colonnes ensemble.
-
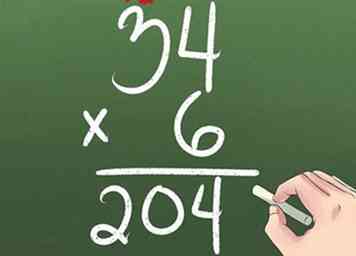 6 Multipliez et regroupez les colonnes.
6 Multipliez et regroupez les colonnes. - Vous voulez multiplier 34 x 6. Vous commencez par multiplier la colonne 1s (4 x 6), mais vous ne pouvez pas avoir 24 1 dans la colonne 1s.
- Gardez 4 1 dans la colonne 1s. Déplacez les 2 10 sur la colonne 10 s.
- Multipliez 6 x 3, ce qui équivaut à 18. Ajoutez les 2 que vous avez reportés, ce qui correspondra à 20.
Partie six de six:
Fondamentaux Mathématiques - Division Découverte
-
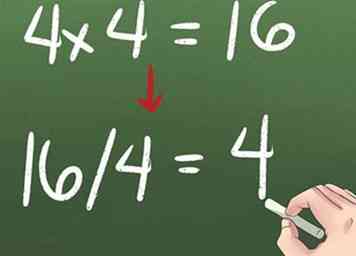 1 Pensez à la division comme l'opposé de la multiplication. Si 4 x 4 = 16, alors 16/4 = 4.
1 Pensez à la division comme l'opposé de la multiplication. Si 4 x 4 = 16, alors 16/4 = 4. -
 2 Écrivez votre problème de division.
2 Écrivez votre problème de division. - Diviser le nombre à gauche du symbole de division, ou le diviseur, dans le premier nombre sous le symbole de division. Puisque 6/2 = 3, vous écrirez 3 au-dessus du symbole de division.
- Multipliez le nombre au-dessus du symbole de division par le diviseur. Apportez le produit sous le premier numéro sous le symbole de la division. Puisque 3 x 2 = 6, alors vous ramènerez un 6.
- Soustrayez les 2 chiffres que vous avez écrits. 6 - 6 = 0. Vous pouvez également laisser le 0 vide, car vous ne lancez généralement pas un nouveau numéro avec 0.
- Apportez le deuxième chiffre sous le symbole de division.
- Divisez le nombre que vous avez amené par le diviseur. Dans ce cas, 8/2 = 4. Écrivez 4 au-dessus du symbole de division.
- Multipliez le nombre en haut à droite par le diviseur et ramenez le nombre. 4 x 2 = 8.
- Soustrayez les nombres. La soustraction finale est égale à zéro, ce qui signifie que vous avez fini le problème. 68/2 = 34.[6]
-
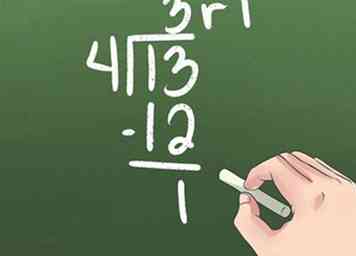 3 Compte pour les restes. Certains diviseurs ne se divisent pas uniformément dans d'autres nombres. Lorsque vous avez terminé votre soustraction finale et que vous n'avez plus de chiffres à afficher, le nombre final est le reste.[7]
3 Compte pour les restes. Certains diviseurs ne se divisent pas uniformément dans d'autres nombres. Lorsque vous avez terminé votre soustraction finale et que vous n'avez plus de chiffres à afficher, le nombre final est le reste.[7]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Présentez-vous en classe. Lorsque vous manquez le cours, vous devez apprendre les concepts d'un camarade de classe ou de votre manuel. Vous n'obtiendrez jamais un aussi bon aperçu de vos amis ou du texte que vous le ferez de votre professeur.
1 Présentez-vous en classe. Lorsque vous manquez le cours, vous devez apprendre les concepts d'un camarade de classe ou de votre manuel. Vous n'obtiendrez jamais un aussi bon aperçu de vos amis ou du texte que vous le ferez de votre professeur.  2 Travaillez avec votre professeur. Si votre professeur a des problèmes à l’avant de votre classe, travaillez avec votre professeur dans votre cahier.
2 Travaillez avec votre professeur. Si votre professeur a des problèmes à l’avant de votre classe, travaillez avec votre professeur dans votre cahier.  3 Faites vos devoirs le jour même où il est assigné. Lorsque vous faites les devoirs le même jour, les concepts sont frais dans votre esprit. Parfois, terminer vos devoirs le même jour n'est pas possible. Assurez-vous que vos devoirs sont complets avant de vous rendre en classe.
3 Faites vos devoirs le jour même où il est assigné. Lorsque vous faites les devoirs le même jour, les concepts sont frais dans votre esprit. Parfois, terminer vos devoirs le même jour n'est pas possible. Assurez-vous que vos devoirs sont complets avant de vous rendre en classe.  4 Faites un effort en dehors des cours si vous avez besoin d'aide. Rendez-vous chez votre professeur pendant sa période libre ou pendant les heures de bureau.
4 Faites un effort en dehors des cours si vous avez besoin d'aide. Rendez-vous chez votre professeur pendant sa période libre ou pendant les heures de bureau.  1 Commencez par l'arithmétique. Dans la plupart des écoles, les élèves travaillent sur l'arithmétique pendant les classes élémentaires. L'arithmétique comprend les principes fondamentaux de l'addition, de la soustraction, de la multiplication et de la division.
1 Commencez par l'arithmétique. Dans la plupart des écoles, les élèves travaillent sur l'arithmétique pendant les classes élémentaires. L'arithmétique comprend les principes fondamentaux de l'addition, de la soustraction, de la multiplication et de la division.  2 Progrès en pré-algèbre. Ce cours fournira les éléments de base dont vous aurez besoin pour résoudre les problèmes d'algèbre ultérieurement.
2 Progrès en pré-algèbre. Ce cours fournira les éléments de base dont vous aurez besoin pour résoudre les problèmes d'algèbre ultérieurement.  3 Avance à l'Algèbre I. Au cours de votre première année d’algèbre, vous apprendrez les symboles de base de l’algèbre. Vous apprendrez également à:
3 Avance à l'Algèbre I. Au cours de votre première année d’algèbre, vous apprendrez les symboles de base de l’algèbre. Vous apprendrez également à:  4 Entrez dans la géométrie. En géométrie, vous apprendrez les propriétés des lignes, des segments, des angles et des formes.[3]
4 Entrez dans la géométrie. En géométrie, vous apprendrez les propriétés des lignes, des segments, des angles et des formes.[3]  5 Prenez Algèbre II. Algèbre II s'appuie sur les concepts que vous avez appris en Algèbre I mais ajoute des sujets plus complexes impliquant des fonctions et des matrices non linéaires plus complexes.
5 Prenez Algèbre II. Algèbre II s'appuie sur les concepts que vous avez appris en Algèbre I mais ajoute des sujets plus complexes impliquant des fonctions et des matrices non linéaires plus complexes.  6 S'attaquer à la trigonométrie. Vous connaissez les mots de trig: sinus, cosinus, tangente, etc. La trigonométrie vous apprendra de nombreuses façons pratiques de calculer des angles et des longueurs de lignes.
6 S'attaquer à la trigonométrie. Vous connaissez les mots de trig: sinus, cosinus, tangente, etc. La trigonométrie vous apprendra de nombreuses façons pratiques de calculer des angles et des longueurs de lignes. 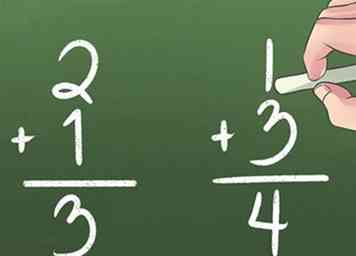 7 Comptez sur des calculs. Le calcul peut sembler intimidant, mais c'est un outil incroyable pour comprendre à la fois le comportement des nombres et le monde qui vous entoure.
7 Comptez sur des calculs. Le calcul peut sembler intimidant, mais c'est un outil incroyable pour comprendre à la fois le comportement des nombres et le monde qui vous entoure. 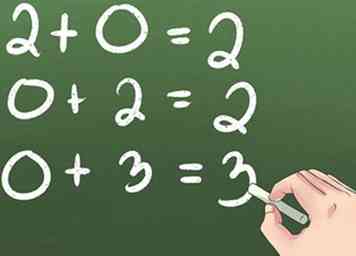 1 Commencez par "+1" faits. L'ajout de 1 à un nombre vous amène au numéro le plus élevé suivant sur la droite numérique. Par exemple, 2 + 1 = 3.
1 Commencez par "+1" faits. L'ajout de 1 à un nombre vous amène au numéro le plus élevé suivant sur la droite numérique. Par exemple, 2 + 1 = 3. 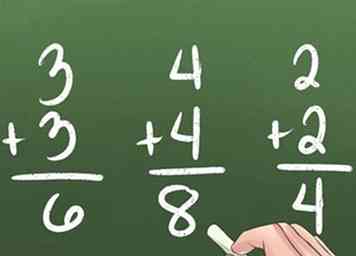 2 Comprendre les zéros. Tout nombre ajouté à zéro est égal au même nombre car "zéro" est identique à "rien".
2 Comprendre les zéros. Tout nombre ajouté à zéro est égal au même nombre car "zéro" est identique à "rien".  3 Apprendre double Les doublons sont des problèmes qui impliquent l'ajout de deux numéros identiques. Par exemple, 3 + 3 = 6 est un exemple d'équation impliquant des doubles.
3 Apprendre double Les doublons sont des problèmes qui impliquent l'ajout de deux numéros identiques. Par exemple, 3 + 3 = 6 est un exemple d'équation impliquant des doubles. 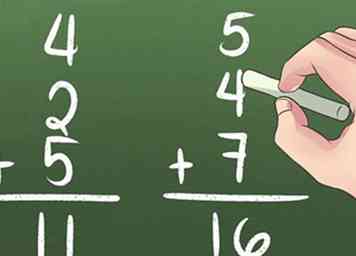 4 Utilisez le mappage pour en savoir plus sur les autres solutions d’ajout. Dans l'exemple ci-dessous, vous apprendrez en mappant ce qui se passe lorsque vous ajoutez 3 à 5, 2 et 1. Essayez les problèmes "ajouter 2" par vous-même.
4 Utilisez le mappage pour en savoir plus sur les autres solutions d’ajout. Dans l'exemple ci-dessous, vous apprendrez en mappant ce qui se passe lorsque vous ajoutez 3 à 5, 2 et 1. Essayez les problèmes "ajouter 2" par vous-même. 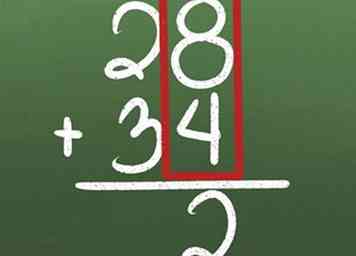 5 Aller au-delà de 10. Apprenez à ajouter 3 nombres ensemble pour obtenir un nombre supérieur à 10.
5 Aller au-delà de 10. Apprenez à ajouter 3 nombres ensemble pour obtenir un nombre supérieur à 10. 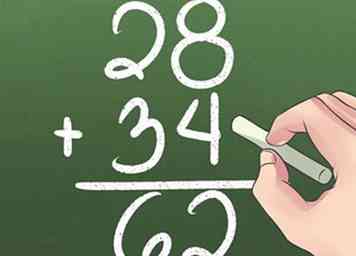 6 Ajouter des nombres plus importants. Apprenez à regrouper les 1 dans les 10 places, les 10 dans les 100, etc.
6 Ajouter des nombres plus importants. Apprenez à regrouper les 1 dans les 10 places, les 10 dans les 100, etc. 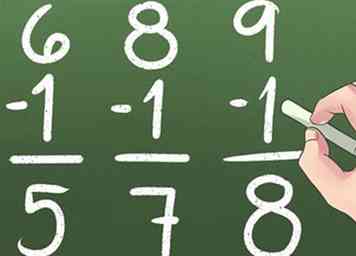 1 Commencez par "en arrière 1."En soustrayant 1 à un nombre, vous retournez à 1 nombre. Par exemple, 4 - 1 = 3.
1 Commencez par "en arrière 1."En soustrayant 1 à un nombre, vous retournez à 1 nombre. Par exemple, 4 - 1 = 3. 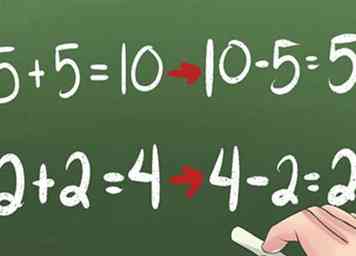 2 Apprendre en double soustraction. Par exemple, vous ajoutez les doubles 5 + 5 pour obtenir 10. Écrivez simplement l'équation en arrière pour obtenir 10 - 5 = 5.
2 Apprendre en double soustraction. Par exemple, vous ajoutez les doubles 5 + 5 pour obtenir 10. Écrivez simplement l'équation en arrière pour obtenir 10 - 5 = 5. 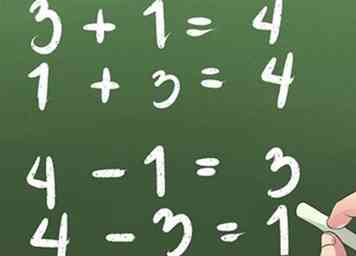 3 Mémoriser les familles de faits. Par exemple:
3 Mémoriser les familles de faits. Par exemple: 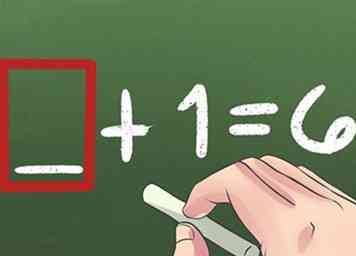 4 Trouvez les numéros manquants. Par exemple, ___ + 1 = 6 (la réponse est 5). Cela pose également les bases de l'algèbre et au-delà.
4 Trouvez les numéros manquants. Par exemple, ___ + 1 = 6 (la réponse est 5). Cela pose également les bases de l'algèbre et au-delà. 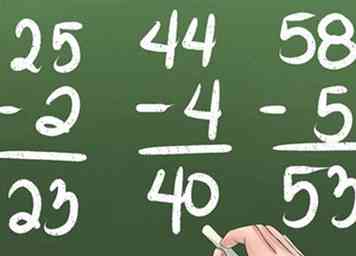 5 Mémoriser les faits de soustraction jusqu'à 20.
5 Mémoriser les faits de soustraction jusqu'à 20.  6 Entraînez-vous à soustraire les nombres à un chiffre des nombres à deux chiffres sans emprunter. Soustrayez les nombres dans la colonne 1 et ramenez le nombre dans la colonne 10s.
6 Entraînez-vous à soustraire les nombres à un chiffre des nombres à deux chiffres sans emprunter. Soustrayez les nombres dans la colonne 1 et ramenez le nombre dans la colonne 10s. 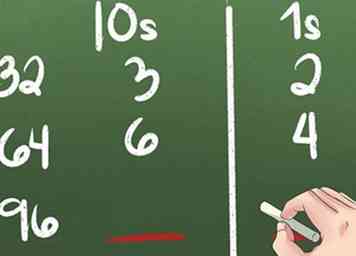 7 Pratiquez la valeur du lieu pour vous préparer à la soustraction avec l'emprunt.
7 Pratiquez la valeur du lieu pour vous préparer à la soustraction avec l'emprunt. 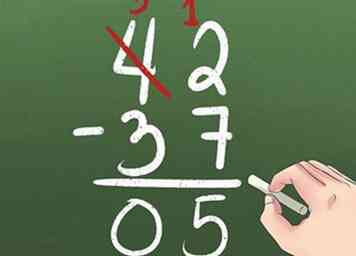 8 Soustraire à l'emprunt.
8 Soustraire à l'emprunt. 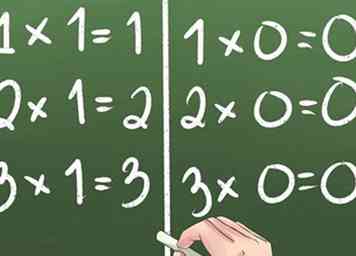 1 Commencez avec 1 et 0. Tout nombre de fois 1 est égal à lui-même. Tout nombre de fois zéro est égal à zéro.
1 Commencez avec 1 et 0. Tout nombre de fois 1 est égal à lui-même. Tout nombre de fois zéro est égal à zéro.  2 Mémorisez la table de multiplication.
2 Mémorisez la table de multiplication. 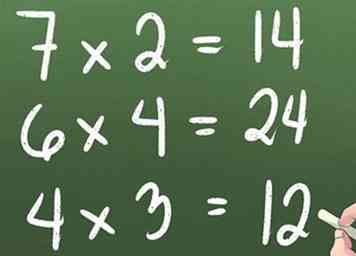 3Pratiquez les problèmes de multiplication à un chiffre
3Pratiquez les problèmes de multiplication à un chiffre 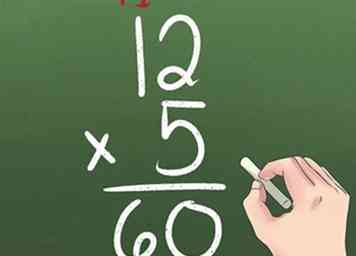 4 Multipliez les nombres à 2 chiffres par les nombres à 1 chiffre.
4 Multipliez les nombres à 2 chiffres par les nombres à 1 chiffre. 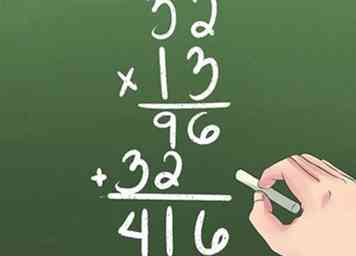 5 Multipliez 2 nombres à 2 chiffres.
5 Multipliez 2 nombres à 2 chiffres. 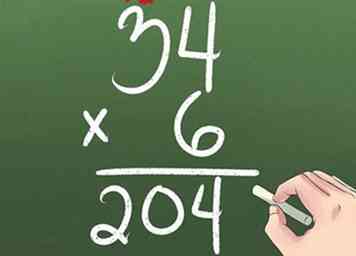 6 Multipliez et regroupez les colonnes.
6 Multipliez et regroupez les colonnes. 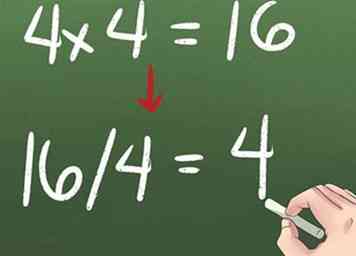 1 Pensez à la division comme l'opposé de la multiplication. Si 4 x 4 = 16, alors 16/4 = 4.
1 Pensez à la division comme l'opposé de la multiplication. Si 4 x 4 = 16, alors 16/4 = 4.  2 Écrivez votre problème de division.
2 Écrivez votre problème de division. 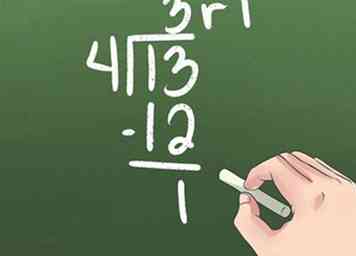 3 Compte pour les restes. Certains diviseurs ne se divisent pas uniformément dans d'autres nombres. Lorsque vous avez terminé votre soustraction finale et que vous n'avez plus de chiffres à afficher, le nombre final est le reste.[7]
3 Compte pour les restes. Certains diviseurs ne se divisent pas uniformément dans d'autres nombres. Lorsque vous avez terminé votre soustraction finale et que vous n'avez plus de chiffres à afficher, le nombre final est le reste.[7]