Vous pouvez multiplier les racines carrées, un type d'expression radicale, tout comme vous pouvez multiplier des nombres entiers. Parfois, les racines carrées ont des coefficients (un entier devant le signe radical), mais cela ne fait qu'ajouter un pas à la multiplication et ne change pas le processus. La partie la plus délicate de la multiplication des racines carrées consiste à simplifier l'expression pour atteindre votre réponse finale, mais même cette étape est facile si vous connaissez vos carrés parfaits.
Méthode One of Two:
Multiplier les racines carrées sans coefficients
-
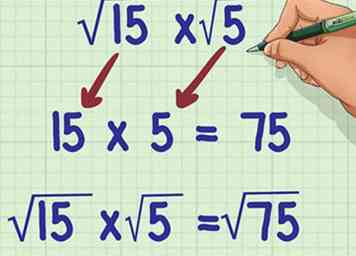 1 Multipliez les radicands. Un radicand est un nombre sous le signe radical.[1] Pour multiplier les radicands, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous un signe radical.[2]
1 Multipliez les radicands. Un radicand est un nombre sous le signe radical.[1] Pour multiplier les radicands, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous un signe radical.[2] - Par exemple, si vous calculez , vous calculeriez . Alors, .
-
 2 Comptez les carrés parfaits dans le radicand. Pour ce faire, voyez si un carré parfait est un facteur du radicand.[3] Si vous ne pouvez pas factoriser un carré parfait, votre réponse est déjà simplifiée et vous ne devez rien faire de plus.
2 Comptez les carrés parfaits dans le radicand. Pour ce faire, voyez si un carré parfait est un facteur du radicand.[3] Si vous ne pouvez pas factoriser un carré parfait, votre réponse est déjà simplifiée et vous ne devez rien faire de plus. - Un carré parfait est le résultat de la multiplication d'un entier (nombre entier positif ou négatif) par lui-même.[4] Par exemple, 25 est un carré parfait, car .
- Par exemple, peut être pris pour sortir le carré parfait 25:
=
-
 3 Placez la racine carrée du carré parfait devant le signe radical. Gardez l'autre facteur sous le signe radical. Cela vous donnera votre expression simplifiée.
3 Placez la racine carrée du carré parfait devant le signe radical. Gardez l'autre facteur sous le signe radical. Cela vous donnera votre expression simplifiée. - Par exemple, peut être considéré comme , donc vous retireriez la racine carrée de 25 (qui est 5):
=
=
- Par exemple, peut être considéré comme , donc vous retireriez la racine carrée de 25 (qui est 5):
-
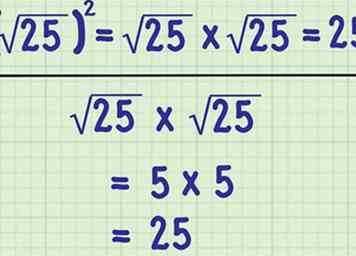 4 Carrez une racine carrée. Dans certains cas, vous devrez multiplier une racine carrée par elle-même. La quadrature d'un nombre et la racine carrée d'un nombre sont des opérations opposées. ainsi, ils se défont. Le résultat de la quadrature d'une racine carrée est donc simplement le nombre sous le signe radical.[5]
4 Carrez une racine carrée. Dans certains cas, vous devrez multiplier une racine carrée par elle-même. La quadrature d'un nombre et la racine carrée d'un nombre sont des opérations opposées. ainsi, ils se défont. Le résultat de la quadrature d'une racine carrée est donc simplement le nombre sous le signe radical.[5] - Par exemple, . Vous obtenez ce résultat parce que .
Méthode deux sur deux:
Multiplier les racines carrées avec des coefficients
-
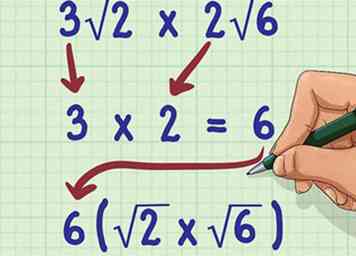 1 Multipliez les coefficients. Un coefficient est un nombre devant le signe radical. Pour ce faire, ignorez simplement le signe radical et radicand et multipliez les deux nombres entiers. Placez leur produit devant le premier signe radical.
1 Multipliez les coefficients. Un coefficient est un nombre devant le signe radical. Pour ce faire, ignorez simplement le signe radical et radicand et multipliez les deux nombres entiers. Placez leur produit devant le premier signe radical. - Faites attention aux signes positifs et négatifs lors de la multiplication des coefficients. N'oubliez pas que les temps négatifs, les positifs sont négatifs et les temps négatifs les négatifs, les positifs.
- Par exemple, si vous calculez , vous devriez d'abord calculer . Alors maintenant, votre problème est .
-
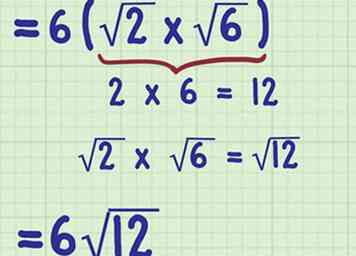 2 Multipliez les radicands. Pour ce faire, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous le signe radical.
2 Multipliez les radicands. Pour ce faire, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous le signe radical. - Par exemple, si le problème est maintenant , pour trouver le produit des radicands, vous calculeriez , alors . Le problème devient maintenant .
-
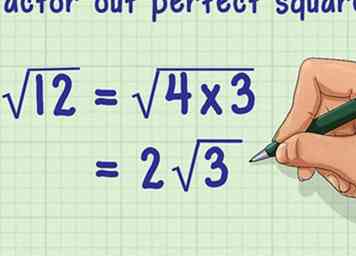 3 Comptez si possible les carrés parfaits dans le radicand. Vous devez le faire pour simplifier votre réponse.[6] Si vous ne pouvez pas sortir un carré parfait, votre réponse est déjà simplifiée et vous pouvez sauter cette étape.
3 Comptez si possible les carrés parfaits dans le radicand. Vous devez le faire pour simplifier votre réponse.[6] Si vous ne pouvez pas sortir un carré parfait, votre réponse est déjà simplifiée et vous pouvez sauter cette étape. - Un carré parfait est le résultat de la multiplication d'un entier (nombre entier positif ou négatif) par lui-même.[7] Par exemple, 4 est un carré parfait, car .
- Par exemple, peut être pris en compte pour sortir le carré parfait 4:
=
-
 4 Multipliez la racine carrée du carré parfait par le coefficient. Gardez l'autre facteur sous le radicand. Cela vous donnera votre expression simplifiée.
4 Multipliez la racine carrée du carré parfait par le coefficient. Gardez l'autre facteur sous le radicand. Cela vous donnera votre expression simplifiée. - Par exemple, peut être considéré comme , donc vous retirez la racine carrée de 4 (qui est 2) et multipliez-la par 6:
=
=
=
- Par exemple, peut être considéré comme , donc vous retirez la racine carrée de 4 (qui est 2) et multipliez-la par 6:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
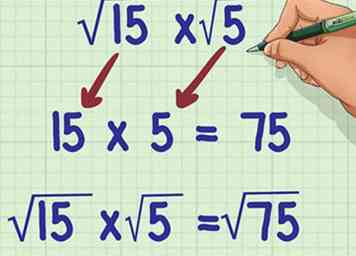 1 Multipliez les radicands. Un radicand est un nombre sous le signe radical.[1] Pour multiplier les radicands, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous un signe radical.[2]
1 Multipliez les radicands. Un radicand est un nombre sous le signe radical.[1] Pour multiplier les radicands, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous un signe radical.[2]  2 Comptez les carrés parfaits dans le radicand. Pour ce faire, voyez si un carré parfait est un facteur du radicand.[3] Si vous ne pouvez pas factoriser un carré parfait, votre réponse est déjà simplifiée et vous ne devez rien faire de plus.
2 Comptez les carrés parfaits dans le radicand. Pour ce faire, voyez si un carré parfait est un facteur du radicand.[3] Si vous ne pouvez pas factoriser un carré parfait, votre réponse est déjà simplifiée et vous ne devez rien faire de plus.  3 Placez la racine carrée du carré parfait devant le signe radical. Gardez l'autre facteur sous le signe radical. Cela vous donnera votre expression simplifiée.
3 Placez la racine carrée du carré parfait devant le signe radical. Gardez l'autre facteur sous le signe radical. Cela vous donnera votre expression simplifiée. 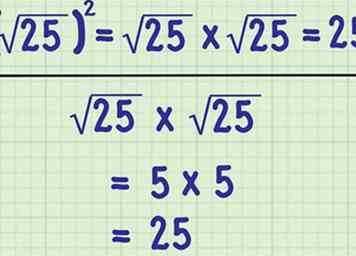 4 Carrez une racine carrée. Dans certains cas, vous devrez multiplier une racine carrée par elle-même. La quadrature d'un nombre et la racine carrée d'un nombre sont des opérations opposées. ainsi, ils se défont. Le résultat de la quadrature d'une racine carrée est donc simplement le nombre sous le signe radical.[5]
4 Carrez une racine carrée. Dans certains cas, vous devrez multiplier une racine carrée par elle-même. La quadrature d'un nombre et la racine carrée d'un nombre sont des opérations opposées. ainsi, ils se défont. Le résultat de la quadrature d'une racine carrée est donc simplement le nombre sous le signe radical.[5] 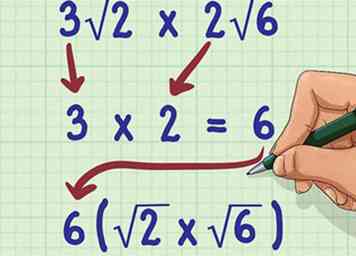 1 Multipliez les coefficients. Un coefficient est un nombre devant le signe radical. Pour ce faire, ignorez simplement le signe radical et radicand et multipliez les deux nombres entiers. Placez leur produit devant le premier signe radical.
1 Multipliez les coefficients. Un coefficient est un nombre devant le signe radical. Pour ce faire, ignorez simplement le signe radical et radicand et multipliez les deux nombres entiers. Placez leur produit devant le premier signe radical. 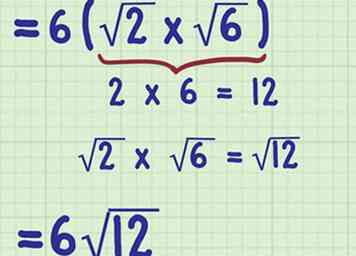 2 Multipliez les radicands. Pour ce faire, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous le signe radical.
2 Multipliez les radicands. Pour ce faire, multipliez les nombres comme s'ils étaient des nombres entiers. Assurez-vous de garder le produit sous le signe radical. 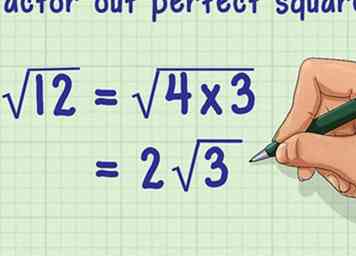 3 Comptez si possible les carrés parfaits dans le radicand. Vous devez le faire pour simplifier votre réponse.[6] Si vous ne pouvez pas sortir un carré parfait, votre réponse est déjà simplifiée et vous pouvez sauter cette étape.
3 Comptez si possible les carrés parfaits dans le radicand. Vous devez le faire pour simplifier votre réponse.[6] Si vous ne pouvez pas sortir un carré parfait, votre réponse est déjà simplifiée et vous pouvez sauter cette étape.  4 Multipliez la racine carrée du carré parfait par le coefficient. Gardez l'autre facteur sous le radicand. Cela vous donnera votre expression simplifiée.
4 Multipliez la racine carrée du carré parfait par le coefficient. Gardez l'autre facteur sous le radicand. Cela vous donnera votre expression simplifiée.