Les réciproques sont utiles dans toutes sortes d'équations algébriques. Par exemple, lorsque vous divisez une fraction par une autre, vous multipliez la première par l'inverse du second. Vous pourriez aussi avoir besoin de réciprocités pour trouver des équations de lignes.
Méthode One of Three:
Recherche de l'inverse d'une fraction ou d'un nombre entier
-
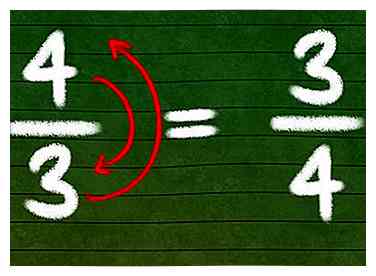 1 Trouvez l'inverse d'une fraction en la retournant. La définition de "réciproque" est simple. Pour trouver l'inverse d'un nombre, calculez simplement "1 ÷ (ce nombre)". Pour une fraction, la réciproque est juste une fraction différente, avec les nombres "renversés" à l'envers (inversés).[1]
1 Trouvez l'inverse d'une fraction en la retournant. La définition de "réciproque" est simple. Pour trouver l'inverse d'un nombre, calculez simplement "1 ÷ (ce nombre)". Pour une fraction, la réciproque est juste une fraction différente, avec les nombres "renversés" à l'envers (inversés).[1] - Par exemple, la réciproque de 3/4 est 4/3.
- Tout nombre de fois sa réciproque vous donnera 1.
-
 2 Écrivez la réciproque d'un nombre entier en tant que fraction. Encore une fois, l'inverse d'un nombre est toujours 1 ÷ (ce nombre). Pour un nombre entier, écrivez cela comme une fraction; il ne sert à rien de le calculer en décimal.
2 Écrivez la réciproque d'un nombre entier en tant que fraction. Encore une fois, l'inverse d'un nombre est toujours 1 ÷ (ce nombre). Pour un nombre entier, écrivez cela comme une fraction; il ne sert à rien de le calculer en décimal. - Par exemple, l'inverse de 2 est 1 ÷ 2 = 1/2.
Méthode deux sur trois:
Recherche de l'inverse d'un nombre mixte
-
 1 Identifiez un nombre fractionnaire. Les nombres mélangés sont des nombres entiers et partiels, tels que 24/5. Il y a deux étapes pour trouver l'inverse d'un nombre mixte, expliqué ci-dessous.
1 Identifiez un nombre fractionnaire. Les nombres mélangés sont des nombres entiers et partiels, tels que 24/5. Il y a deux étapes pour trouver l'inverse d'un nombre mixte, expliqué ci-dessous. -
 2 Changez-le en une fraction impropre. Rappelez-vous que le nombre 1 peut toujours être écrit sous la forme (nombre) / (le même nombre) et que les fractions ayant le même dénominateur (nombre inférieur) peuvent être additionnées. Voici un exemple avec 24/5:
2 Changez-le en une fraction impropre. Rappelez-vous que le nombre 1 peut toujours être écrit sous la forme (nombre) / (le même nombre) et que les fractions ayant le même dénominateur (nombre inférieur) peuvent être additionnées. Voici un exemple avec 24/5: - 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
-
 3 Retournez la fraction. Une fois que le nombre est entièrement écrit en fraction, vous pouvez trouver la réciproque comme vous le feriez avec n'importe quelle fraction: en la retournant.
3 Retournez la fraction. Une fois que le nombre est entièrement écrit en fraction, vous pouvez trouver la réciproque comme vous le feriez avec n'importe quelle fraction: en la retournant. - Dans l'exemple ci-dessus, l'inverse de 14/5 est 5/14.
Méthode trois sur trois:
Trouver l'inverse d'un nombre décimal
-
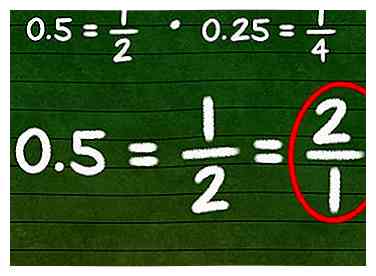 1 Changez-le en une fraction si possible. Vous pouvez reconnaître certains nombres décimaux courants qui peuvent facilement être transformés en fractions. Par exemple, 0.5 = 1/2et 0,25 = 1/4. Une fois sous forme de fraction, retournez simplement la fraction pour trouver la réciproque.
1 Changez-le en une fraction si possible. Vous pouvez reconnaître certains nombres décimaux courants qui peuvent facilement être transformés en fractions. Par exemple, 0.5 = 1/2et 0,25 = 1/4. Une fois sous forme de fraction, retournez simplement la fraction pour trouver la réciproque. - Par exemple, l'inverse de 0.5 est 2/1 = 2.
-
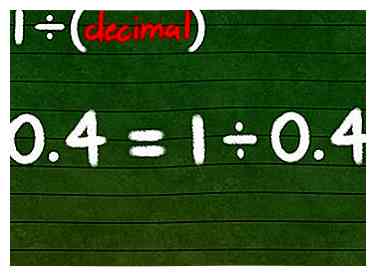 2 Ecrivez un problème de division. Si vous ne pouvez pas le changer en fraction, calculez l'inverse de ce nombre en tant que problème de division: 1 ÷ (la décimale). Vous pouvez utiliser une calculatrice pour résoudre ce problème ou passer à l'étape suivante pour le résoudre manuellement.
2 Ecrivez un problème de division. Si vous ne pouvez pas le changer en fraction, calculez l'inverse de ce nombre en tant que problème de division: 1 ÷ (la décimale). Vous pouvez utiliser une calculatrice pour résoudre ce problème ou passer à l'étape suivante pour le résoudre manuellement. - Par exemple, vous pouvez trouver l'inverse de 0,4 en calculant 1 ÷ 0,4.
-
 3 Modifiez le problème de division pour utiliser des nombres entiers. La première étape pour diviser les nombres décimaux consiste à déplacer le point décimal jusqu'à ce que tous les nombres impliqués soient des nombres entiers. Tant que vous déplacez le point décimal du même nombre d'espaces pour les deux nombres, vous obtenez la bonne réponse.
3 Modifiez le problème de division pour utiliser des nombres entiers. La première étape pour diviser les nombres décimaux consiste à déplacer le point décimal jusqu'à ce que tous les nombres impliqués soient des nombres entiers. Tant que vous déplacez le point décimal du même nombre d'espaces pour les deux nombres, vous obtenez la bonne réponse. - Par exemple, vous pouvez prendre 1 ÷ 0,4 et le réécrire en 10 ÷ 4. Dans ce cas, vous avez déplacé chaque décimale d'un espace vers la droite, ce qui revient à multiplier chaque nombre par dix.
-
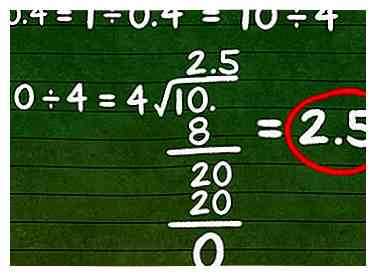 4 Résoudre le problème en utilisant la division longue. Utilisez des techniques de division longue pour calculer la réciproque. Si vous le calculez pour 10 ÷ 4, vous aurez la réponse 2.5, l'inverse de 0,4.
4 Résoudre le problème en utilisant la division longue. Utilisez des techniques de division longue pour calculer la réciproque. Si vous le calculez pour 10 ÷ 4, vous aurez la réponse 2.5, l'inverse de 0,4.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
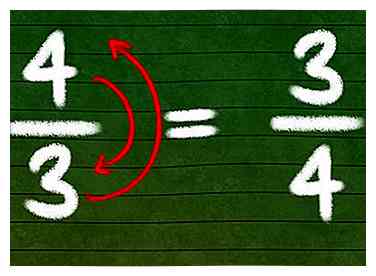 1 Trouvez l'inverse d'une fraction en la retournant. La définition de "réciproque" est simple. Pour trouver l'inverse d'un nombre, calculez simplement "1 ÷ (ce nombre)". Pour une fraction, la réciproque est juste une fraction différente, avec les nombres "renversés" à l'envers (inversés).[1]
1 Trouvez l'inverse d'une fraction en la retournant. La définition de "réciproque" est simple. Pour trouver l'inverse d'un nombre, calculez simplement "1 ÷ (ce nombre)". Pour une fraction, la réciproque est juste une fraction différente, avec les nombres "renversés" à l'envers (inversés).[1]  2 Écrivez la réciproque d'un nombre entier en tant que fraction. Encore une fois, l'inverse d'un nombre est toujours 1 ÷ (ce nombre). Pour un nombre entier, écrivez cela comme une fraction; il ne sert à rien de le calculer en décimal.
2 Écrivez la réciproque d'un nombre entier en tant que fraction. Encore une fois, l'inverse d'un nombre est toujours 1 ÷ (ce nombre). Pour un nombre entier, écrivez cela comme une fraction; il ne sert à rien de le calculer en décimal.  1 Identifiez un nombre fractionnaire. Les nombres mélangés sont des nombres entiers et partiels, tels que 24/5. Il y a deux étapes pour trouver l'inverse d'un nombre mixte, expliqué ci-dessous.
1 Identifiez un nombre fractionnaire. Les nombres mélangés sont des nombres entiers et partiels, tels que 24/5. Il y a deux étapes pour trouver l'inverse d'un nombre mixte, expliqué ci-dessous.  2 Changez-le en une fraction impropre. Rappelez-vous que le nombre 1 peut toujours être écrit sous la forme (nombre) / (le même nombre) et que les fractions ayant le même dénominateur (nombre inférieur) peuvent être additionnées. Voici un exemple avec 24/5:
2 Changez-le en une fraction impropre. Rappelez-vous que le nombre 1 peut toujours être écrit sous la forme (nombre) / (le même nombre) et que les fractions ayant le même dénominateur (nombre inférieur) peuvent être additionnées. Voici un exemple avec 24/5:  3 Retournez la fraction. Une fois que le nombre est entièrement écrit en fraction, vous pouvez trouver la réciproque comme vous le feriez avec n'importe quelle fraction: en la retournant.
3 Retournez la fraction. Une fois que le nombre est entièrement écrit en fraction, vous pouvez trouver la réciproque comme vous le feriez avec n'importe quelle fraction: en la retournant. 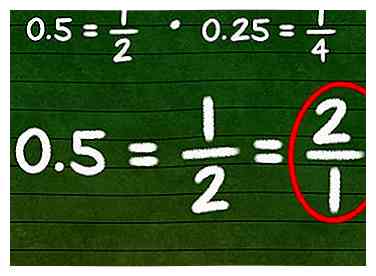 1 Changez-le en une fraction si possible. Vous pouvez reconnaître certains nombres décimaux courants qui peuvent facilement être transformés en fractions. Par exemple, 0.5 = 1/2et 0,25 = 1/4. Une fois sous forme de fraction, retournez simplement la fraction pour trouver la réciproque.
1 Changez-le en une fraction si possible. Vous pouvez reconnaître certains nombres décimaux courants qui peuvent facilement être transformés en fractions. Par exemple, 0.5 = 1/2et 0,25 = 1/4. Une fois sous forme de fraction, retournez simplement la fraction pour trouver la réciproque. 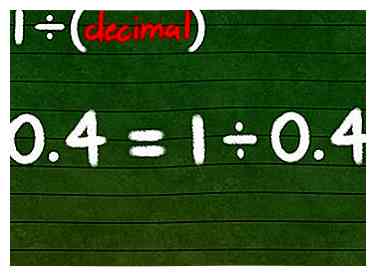 2 Ecrivez un problème de division. Si vous ne pouvez pas le changer en fraction, calculez l'inverse de ce nombre en tant que problème de division: 1 ÷ (la décimale). Vous pouvez utiliser une calculatrice pour résoudre ce problème ou passer à l'étape suivante pour le résoudre manuellement.
2 Ecrivez un problème de division. Si vous ne pouvez pas le changer en fraction, calculez l'inverse de ce nombre en tant que problème de division: 1 ÷ (la décimale). Vous pouvez utiliser une calculatrice pour résoudre ce problème ou passer à l'étape suivante pour le résoudre manuellement.  3 Modifiez le problème de division pour utiliser des nombres entiers. La première étape pour diviser les nombres décimaux consiste à déplacer le point décimal jusqu'à ce que tous les nombres impliqués soient des nombres entiers. Tant que vous déplacez le point décimal du même nombre d'espaces pour les deux nombres, vous obtenez la bonne réponse.
3 Modifiez le problème de division pour utiliser des nombres entiers. La première étape pour diviser les nombres décimaux consiste à déplacer le point décimal jusqu'à ce que tous les nombres impliqués soient des nombres entiers. Tant que vous déplacez le point décimal du même nombre d'espaces pour les deux nombres, vous obtenez la bonne réponse. 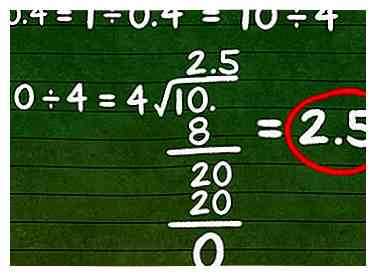 4 Résoudre le problème en utilisant la division longue. Utilisez des techniques de division longue pour calculer la réciproque. Si vous le calculez pour 10 ÷ 4, vous aurez la réponse 2.5, l'inverse de 0,4.
4 Résoudre le problème en utilisant la division longue. Utilisez des techniques de division longue pour calculer la réciproque. Si vous le calculez pour 10 ÷ 4, vous aurez la réponse 2.5, l'inverse de 0,4.