Le symbole radical (√) représente la racine carrée d'un nombre. Vous pouvez rencontrer le symbole radical en algèbre ou même en menuiserie ou dans un autre métier qui implique la géométrie ou le calcul des tailles ou des distances relatives. Vous pouvez multiplier deux radicaux ayant les mêmes indices (degrés d'une racine). Si les radicaux n'ont pas les mêmes indices, vous pouvez manipuler l'équation jusqu'à ce qu'ils le fassent. Si vous voulez savoir comment multiplier des radicaux avec ou sans coefficients, suivez ces étapes.
Méthode One of Three:
Multiplier les radicaux sans coefficients
-
 1 Assurez-vous que les radicaux ont le même index. Pour multiplier les radicaux en utilisant la méthode de base, ils doivent avoir le même index. L'index est le très petit nombre écrit juste à gauche de la ligne supérieure du symbole radical. S'il n'y a pas de numéro d'index, le radical est considéré comme une racine carrée (index 2) et peut être multiplié par d'autres racines carrées. Vous pouvez multiplier des radicaux avec des index différents, mais c'est une méthode plus avancée qui sera expliquée plus tard. Voici deux exemples de multiplication utilisant des radicaux avec les mêmes index:
1 Assurez-vous que les radicaux ont le même index. Pour multiplier les radicaux en utilisant la méthode de base, ils doivent avoir le même index. L'index est le très petit nombre écrit juste à gauche de la ligne supérieure du symbole radical. S'il n'y a pas de numéro d'index, le radical est considéré comme une racine carrée (index 2) et peut être multiplié par d'autres racines carrées. Vous pouvez multiplier des radicaux avec des index différents, mais c'est une méthode plus avancée qui sera expliquée plus tard. Voici deux exemples de multiplication utilisant des radicaux avec les mêmes index: - Ex. 1: √ (18) x √ (2) =?
- Ex. 2: √ (10) x √ (5) =?
- Ex. 3: 3√ (3) x 3√(9) = ?
-
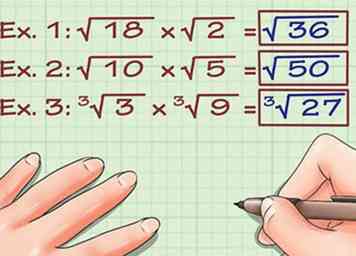 2 Multipliez les nombres sous les signes radicaux. Ensuite, multipliez simplement les nombres sous les signes de racine ou de racine carrée et conservez-les. Voici comment vous le faites:
2 Multipliez les nombres sous les signes radicaux. Ensuite, multipliez simplement les nombres sous les signes de racine ou de racine carrée et conservez-les. Voici comment vous le faites: - Ex. 1: √ (18) x √ (2) = √ (36)
- Ex. 2: √ (10) x √ (5) = √ (50)
- Ex. 3: 3√ (3) x 3√(9) = 3√(27)
-
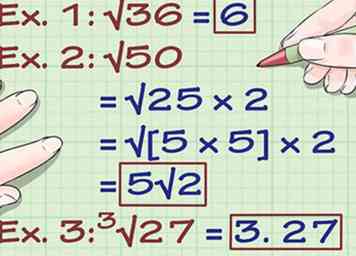 3 Simplifiez les expressions radicales. Si vous avez multiplié les radicaux, il y a de fortes chances qu'ils puissent être simplifiés pour obtenir des carrés parfaits ou des cubes parfaits, ou qu'ils puissent être simplifiés en trouvant un carré parfait comme facteur du produit final. Voici comment vous le faites:
3 Simplifiez les expressions radicales. Si vous avez multiplié les radicaux, il y a de fortes chances qu'ils puissent être simplifiés pour obtenir des carrés parfaits ou des cubes parfaits, ou qu'ils puissent être simplifiés en trouvant un carré parfait comme facteur du produit final. Voici comment vous le faites: - Ex. 1: √ (36) = 6. 36 est un carré parfait car c'est le produit de 6 x 6. La racine carrée de 36 est simplement 6.
- Ex. 2: √ (50) = √ (25 x 2) = √ ([5 x 5] x 2) = 5√ (2). Bien que 50 ne soit pas un carré parfait, 25 est un facteur de 50 (car il se divise uniformément dans le nombre) et est un carré parfait. Vous pouvez diviser 25 en ses facteurs, 5 x 5, et déplacer un 5 du signe racine carrée pour simplifier l'expression.
- Vous pouvez penser à ceci: Si vous jetez le 5 sous le radical, il se multiplie par lui-même et redevient 25.
- Ex. 3:3√ (27) = 3. 27 est un cube parfait car c'est le produit de 3 x 3 x 3. La racine cubique de 27 est donc 3.
Méthode deux sur trois:
Multiplier les radicaux avec des coefficients
-
 1 Multipliez les coefficients. Les coefficients sont les nombres en dehors d'un radical. S'il n'y a pas de coefficient donné, alors le coefficient peut être compris comme étant 1. Multipliez les coefficients ensemble. Voici comment vous le faites:
1 Multipliez les coefficients. Les coefficients sont les nombres en dehors d'un radical. S'il n'y a pas de coefficient donné, alors le coefficient peut être compris comme étant 1. Multipliez les coefficients ensemble. Voici comment vous le faites: - Ex. 1: 3√ (2) x √ (10) = 3√ (?)
- 3 x 1 = 3
- Ex. 2: 4√ (3) x 3√ (6) = 12√ (?)
- 4 x 3 = 12
- Ex. 1: 3√ (2) x √ (10) = 3√ (?)
-
 2 Multipliez les nombres à l'intérieur des radicaux. Après avoir multiplié les coefficients, vous pouvez multiplier les nombres à l'intérieur des radicaux. Voici comment vous le faites:
2 Multipliez les nombres à l'intérieur des radicaux. Après avoir multiplié les coefficients, vous pouvez multiplier les nombres à l'intérieur des radicaux. Voici comment vous le faites: - Ex. 1: 3√ (2) x √ (10) = 3√ (2 x 10) = 3√ (20)
- Ex. 2: 4√ (3) x 3√ (6) = 12√ (3 x 6) = 12√ (18)
-
 3 Simplifiez le produit. Ensuite, simplifiez les nombres sous les radicaux en recherchant des carrés parfaits ou des multiples des nombres sous les radicaux qui sont des carrés parfaits. Une fois que vous avez simplifié ces termes, multipliez-les simplement par leurs coefficients correspondants. Voici comment vous le faites:
3 Simplifiez le produit. Ensuite, simplifiez les nombres sous les radicaux en recherchant des carrés parfaits ou des multiples des nombres sous les radicaux qui sont des carrés parfaits. Une fois que vous avez simplifié ces termes, multipliez-les simplement par leurs coefficients correspondants. Voici comment vous le faites: - 3√ (20) = 3√ (4 x 5) = 3√ ([2 x 2] x 5) = (3 x 2) √ (5) = 6√ (5)
- 12√ (18) = 12√ (9 x 2) = 12√ (3 x 3 x 2) = (12 x 3) √ (2) = 36√ (2)
Méthode trois sur trois:
Multiplier les radicaux avec différents indices
-
 1 Trouvez le LCM (multiple commun le plus bas) des indices. Pour trouver le LCM des index, trouvez le plus petit nombre qui soit divisible par les deux indices. Trouvez le LCM des indices pour l'équation suivante:3√ (5) x 2√(2) = ?
1 Trouvez le LCM (multiple commun le plus bas) des indices. Pour trouver le LCM des index, trouvez le plus petit nombre qui soit divisible par les deux indices. Trouvez le LCM des indices pour l'équation suivante:3√ (5) x 2√(2) = ? - Les indices sont 3 et 2. 6 est le LCM de ces deux nombres parce que c'est le plus petit nombre qui est divisible par 3 et 2. 6/3 = 2 et 6/2 = 3. Pour multiplier les radicaux, tous deux de les indices devront être 6.
-
 2 Ecrivez chaque expression avec le nouveau LCM comme index. Voici à quoi ressembleraient les expressions dans l'équation avec leurs nouveaux index:
2 Ecrivez chaque expression avec le nouveau LCM comme index. Voici à quoi ressembleraient les expressions dans l'équation avec leurs nouveaux index: - 6√ (5) x 6√(2) = ?
-
 3 Recherchez le nombre dont vous avez besoin pour multiplier chaque index original par afin de trouver le LCM. Pour l'expression 3√ (5), il faudrait multiplier l’indice de 3 par 2 pour obtenir 6. Pour l’expression 2√ (2), vous devez multiplier l’indice de 2 par 3 pour obtenir 6.
3 Recherchez le nombre dont vous avez besoin pour multiplier chaque index original par afin de trouver le LCM. Pour l'expression 3√ (5), il faudrait multiplier l’indice de 3 par 2 pour obtenir 6. Pour l’expression 2√ (2), vous devez multiplier l’indice de 2 par 3 pour obtenir 6. -
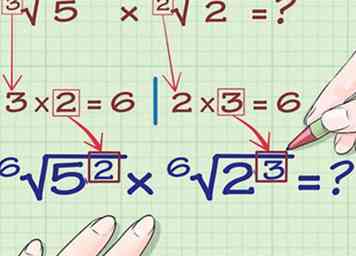 4 Faites de ce nombre l'exposant du nombre à l'intérieur du radical. Pour la première équation, faites le nombre 2 l'exposant sur le nombre 5. Pour la deuxième équation, faites le nombre 3 l'exposant sur le nombre 2. Voici à quoi cela ressemblerait:
4 Faites de ce nombre l'exposant du nombre à l'intérieur du radical. Pour la première équation, faites le nombre 2 l'exposant sur le nombre 5. Pour la deuxième équation, faites le nombre 3 l'exposant sur le nombre 2. Voici à quoi cela ressemblerait: - 2 --> 6√(5) = 6√(5)2
- 3 --> 6√(2) = 6√(2)3
-
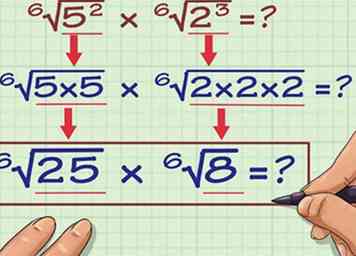 5 Multipliez les nombres à l'intérieur des radicaux par leurs exposants. Voici comment vous le faites:
5 Multipliez les nombres à l'intérieur des radicaux par leurs exposants. Voici comment vous le faites: - 6√(5)2 = 6√ (5 x 5) = 6√25
- 6√(2)3 = 6√ (2 x 2 x 2) = 6√8
-
 6 Placez ces nombres sous un radical. Placez-les sous un radical et connectez-les avec un signe de multiplication. Voici à quoi ressemblerait le résultat: 6√ (8 x 25)
6 Placez ces nombres sous un radical. Placez-les sous un radical et connectez-les avec un signe de multiplication. Voici à quoi ressemblerait le résultat: 6√ (8 x 25) -
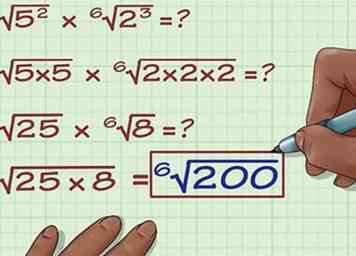 7 Multipliez-les. 6√ (8 x 25) = 6√ (200). C'est la réponse finale.Dans certains cas, vous pouvez simplifier ces expressions - par exemple, vous pouvez simplifier cette expression si vous avez trouvé un nombre pouvant être multiplié par six, soit un facteur de 200. Mais dans ce cas, l'expression ne peut pas être multipliée. être simplifié davantage.
7 Multipliez-les. 6√ (8 x 25) = 6√ (200). C'est la réponse finale.Dans certains cas, vous pouvez simplifier ces expressions - par exemple, vous pouvez simplifier cette expression si vous avez trouvé un nombre pouvant être multiplié par six, soit un facteur de 200. Mais dans ce cas, l'expression ne peut pas être multipliée. être simplifié davantage.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Assurez-vous que les radicaux ont le même index. Pour multiplier les radicaux en utilisant la méthode de base, ils doivent avoir le même index. L'index est le très petit nombre écrit juste à gauche de la ligne supérieure du symbole radical. S'il n'y a pas de numéro d'index, le radical est considéré comme une racine carrée (index 2) et peut être multiplié par d'autres racines carrées. Vous pouvez multiplier des radicaux avec des index différents, mais c'est une méthode plus avancée qui sera expliquée plus tard. Voici deux exemples de multiplication utilisant des radicaux avec les mêmes index:
1 Assurez-vous que les radicaux ont le même index. Pour multiplier les radicaux en utilisant la méthode de base, ils doivent avoir le même index. L'index est le très petit nombre écrit juste à gauche de la ligne supérieure du symbole radical. S'il n'y a pas de numéro d'index, le radical est considéré comme une racine carrée (index 2) et peut être multiplié par d'autres racines carrées. Vous pouvez multiplier des radicaux avec des index différents, mais c'est une méthode plus avancée qui sera expliquée plus tard. Voici deux exemples de multiplication utilisant des radicaux avec les mêmes index: 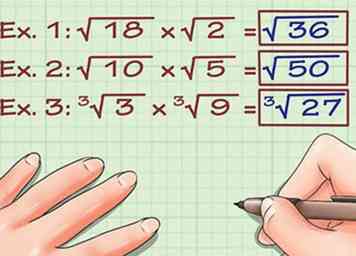 2 Multipliez les nombres sous les signes radicaux. Ensuite, multipliez simplement les nombres sous les signes de racine ou de racine carrée et conservez-les. Voici comment vous le faites:
2 Multipliez les nombres sous les signes radicaux. Ensuite, multipliez simplement les nombres sous les signes de racine ou de racine carrée et conservez-les. Voici comment vous le faites: 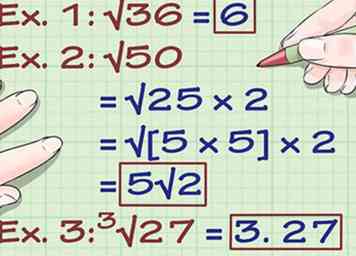 3 Simplifiez les expressions radicales. Si vous avez multiplié les radicaux, il y a de fortes chances qu'ils puissent être simplifiés pour obtenir des carrés parfaits ou des cubes parfaits, ou qu'ils puissent être simplifiés en trouvant un carré parfait comme facteur du produit final. Voici comment vous le faites:
3 Simplifiez les expressions radicales. Si vous avez multiplié les radicaux, il y a de fortes chances qu'ils puissent être simplifiés pour obtenir des carrés parfaits ou des cubes parfaits, ou qu'ils puissent être simplifiés en trouvant un carré parfait comme facteur du produit final. Voici comment vous le faites:  1 Multipliez les coefficients. Les coefficients sont les nombres en dehors d'un radical. S'il n'y a pas de coefficient donné, alors le coefficient peut être compris comme étant 1. Multipliez les coefficients ensemble. Voici comment vous le faites:
1 Multipliez les coefficients. Les coefficients sont les nombres en dehors d'un radical. S'il n'y a pas de coefficient donné, alors le coefficient peut être compris comme étant 1. Multipliez les coefficients ensemble. Voici comment vous le faites:  2 Multipliez les nombres à l'intérieur des radicaux. Après avoir multiplié les coefficients, vous pouvez multiplier les nombres à l'intérieur des radicaux. Voici comment vous le faites:
2 Multipliez les nombres à l'intérieur des radicaux. Après avoir multiplié les coefficients, vous pouvez multiplier les nombres à l'intérieur des radicaux. Voici comment vous le faites:  3 Simplifiez le produit. Ensuite, simplifiez les nombres sous les radicaux en recherchant des carrés parfaits ou des multiples des nombres sous les radicaux qui sont des carrés parfaits. Une fois que vous avez simplifié ces termes, multipliez-les simplement par leurs coefficients correspondants. Voici comment vous le faites:
3 Simplifiez le produit. Ensuite, simplifiez les nombres sous les radicaux en recherchant des carrés parfaits ou des multiples des nombres sous les radicaux qui sont des carrés parfaits. Une fois que vous avez simplifié ces termes, multipliez-les simplement par leurs coefficients correspondants. Voici comment vous le faites:  1 Trouvez le LCM (multiple commun le plus bas) des indices. Pour trouver le LCM des index, trouvez le plus petit nombre qui soit divisible par les deux indices. Trouvez le LCM des indices pour l'équation suivante:3√ (5) x 2√(2) = ?
1 Trouvez le LCM (multiple commun le plus bas) des indices. Pour trouver le LCM des index, trouvez le plus petit nombre qui soit divisible par les deux indices. Trouvez le LCM des indices pour l'équation suivante:3√ (5) x 2√(2) = ?  2 Ecrivez chaque expression avec le nouveau LCM comme index. Voici à quoi ressembleraient les expressions dans l'équation avec leurs nouveaux index:
2 Ecrivez chaque expression avec le nouveau LCM comme index. Voici à quoi ressembleraient les expressions dans l'équation avec leurs nouveaux index:  3 Recherchez le nombre dont vous avez besoin pour multiplier chaque index original par afin de trouver le LCM. Pour l'expression 3√ (5), il faudrait multiplier l’indice de 3 par 2 pour obtenir 6. Pour l’expression 2√ (2), vous devez multiplier l’indice de 2 par 3 pour obtenir 6.
3 Recherchez le nombre dont vous avez besoin pour multiplier chaque index original par afin de trouver le LCM. Pour l'expression 3√ (5), il faudrait multiplier l’indice de 3 par 2 pour obtenir 6. Pour l’expression 2√ (2), vous devez multiplier l’indice de 2 par 3 pour obtenir 6. 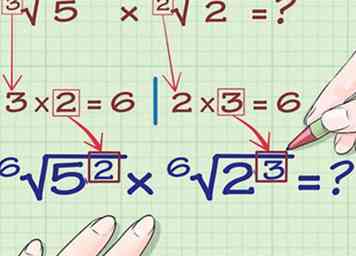 4 Faites de ce nombre l'exposant du nombre à l'intérieur du radical. Pour la première équation, faites le nombre 2 l'exposant sur le nombre 5. Pour la deuxième équation, faites le nombre 3 l'exposant sur le nombre 2. Voici à quoi cela ressemblerait:
4 Faites de ce nombre l'exposant du nombre à l'intérieur du radical. Pour la première équation, faites le nombre 2 l'exposant sur le nombre 5. Pour la deuxième équation, faites le nombre 3 l'exposant sur le nombre 2. Voici à quoi cela ressemblerait: 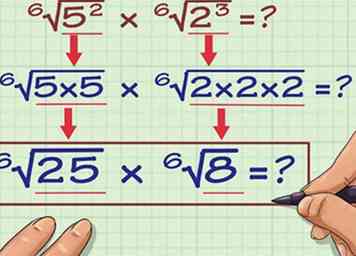 5 Multipliez les nombres à l'intérieur des radicaux par leurs exposants. Voici comment vous le faites:
5 Multipliez les nombres à l'intérieur des radicaux par leurs exposants. Voici comment vous le faites:  6 Placez ces nombres sous un radical. Placez-les sous un radical et connectez-les avec un signe de multiplication. Voici à quoi ressemblerait le résultat: 6√ (8 x 25)
6 Placez ces nombres sous un radical. Placez-les sous un radical et connectez-les avec un signe de multiplication. Voici à quoi ressemblerait le résultat: 6√ (8 x 25) 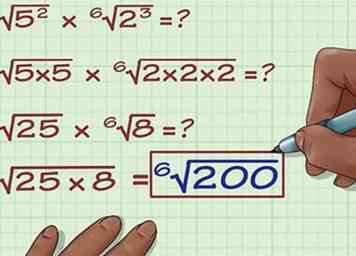 7 Multipliez-les. 6√ (8 x 25) = 6√ (200). C'est la réponse finale.Dans certains cas, vous pouvez simplifier ces expressions - par exemple, vous pouvez simplifier cette expression si vous avez trouvé un nombre pouvant être multiplié par six, soit un facteur de 200. Mais dans ce cas, l'expression ne peut pas être multipliée. être simplifié davantage.
7 Multipliez-les. 6√ (8 x 25) = 6√ (200). C'est la réponse finale.Dans certains cas, vous pouvez simplifier ces expressions - par exemple, vous pouvez simplifier cette expression si vous avez trouvé un nombre pouvant être multiplié par six, soit un facteur de 200. Mais dans ce cas, l'expression ne peut pas être multipliée. être simplifié davantage.