L'utilisation de l'algorithme standard pour multiplier deux nombres à deux chiffres suffit dans la plupart des cas; Cependant, ses multiples étapes peuvent vous permettre de rechercher rapidement et facilement le produit de ces types de numéros. Si vous connaissez vos faits mathématiques de base et que vous avez un bon sens des nombres, vous pouvez utiliser plusieurs techniques pour multiplier mentalement deux nombres à deux chiffres. Si vous connaissez la différence de deux carrés, vous pouvez modifier vos deux facteurs pour qu'ils correspondent à cette formule algébrique. Vous pouvez également manipuler les facteurs en utilisant la propriété distributive, ou en doublant et divisant par deux, jusqu'à ce que vous obteniez deux nouveaux nombres plus faciles à utiliser.
Méthode One of Three:
Trouver la différence entre deux carrés
-
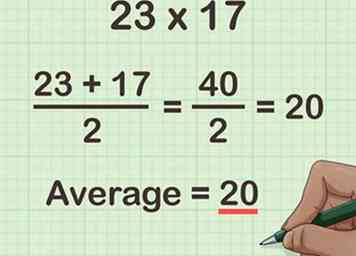 1 Trouvez la moyenne des deux facteurs que vous multipliez. Pour trouver la moyenne, ajoutez les deux nombres ensemble, puis divisez par 2. Vous pouvez également considérer cela comme le nombre dont les deux facteurs sont équidistants.[1]
1 Trouvez la moyenne des deux facteurs que vous multipliez. Pour trouver la moyenne, ajoutez les deux nombres ensemble, puis divisez par 2. Vous pouvez également considérer cela comme le nombre dont les deux facteurs sont équidistants.[1] - Notez que cette méthode ne fonctionne que si la moyenne des deux facteurs est un nombre entier.
- Par exemple, si vous calculez , trouvez la moyenne de 23 et 17:
Donc, la moyenne est 20. En d'autres termes, 23 et 17 sont équidistants de 20.
-
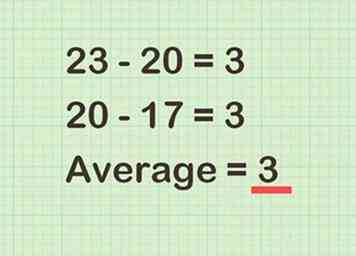 2 Trouvez la différence entre chaque facteur et leur moyenne. Cette différence devrait être la même pour les deux nombres.
2 Trouvez la différence entre chaque facteur et leur moyenne. Cette différence devrait être la même pour les deux nombres. - Par exemple, puisque la moyenne de 23 et 17 est de 20, vous calculez et . Donc, la différence entre chaque facteur et leur moyenne est de 3.
-
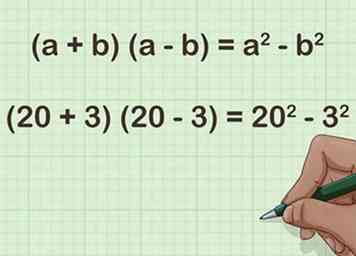 3 Rappelez-vous la formule pour la différence de deux carrés. La formule est [2] Aux fins de multiplier deux nombres à deux chiffres, laissez égal à la moyenne des deux produits, et égale la différence entre chaque facteur et leur moyenne.[3]
3 Rappelez-vous la formule pour la différence de deux carrés. La formule est [2] Aux fins de multiplier deux nombres à deux chiffres, laissez égal à la moyenne des deux produits, et égale la différence entre chaque facteur et leur moyenne.[3] - Par exemple, .
-
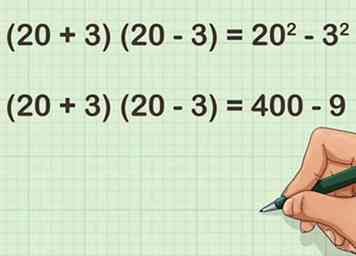 4 Carré et . Rappelez-vous que la quadrature d'un nombre signifie le multiplier par lui-même. J'espère que ces chiffres vous seront faciles à comprendre. Si ce n'est pas le cas, vous devrez peut-être utiliser une autre méthode de calcul mental.
4 Carré et . Rappelez-vous que la quadrature d'un nombre signifie le multiplier par lui-même. J'espère que ces chiffres vous seront faciles à comprendre. Si ce n'est pas le cas, vous devrez peut-être utiliser une autre méthode de calcul mental. - Par exemple:
- Par exemple:
-
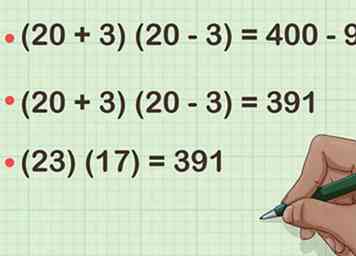 5 Calculez la différence entre les deux carrés. Le résultat sera le produit de vos deux facteurs d'origine.[4]
5 Calculez la différence entre les deux carrés. Le résultat sera le produit de vos deux facteurs d'origine.[4] - Par exemple, . Alors, .
Méthode deux sur trois:
Utilisation de la propriété distributive
-
 1 Déterminer quel facteur est le plus proche de 100. Cette méthode fonctionne mieux lorsque l’un des facteurs est très proche de 100, en particulier si l’un des facteurs est 99.[5]Mais cette méthode peut également fonctionner pour d'autres facteurs.
1 Déterminer quel facteur est le plus proche de 100. Cette méthode fonctionne mieux lorsque l’un des facteurs est très proche de 100, en particulier si l’un des facteurs est 99.[5]Mais cette méthode peut également fonctionner pour d'autres facteurs. - Par exemple, vous pourriez multiplier . Dans ce cas, 98 est le plus proche de 100.
-
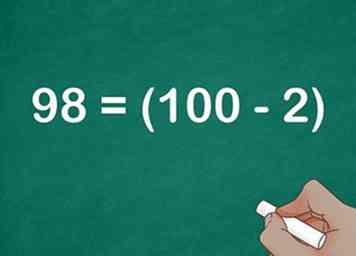 2 Ré-exprimer le facteur le plus proche de 100 comme . La variable représente la différence entre le facteur et 100.[6]
2 Ré-exprimer le facteur le plus proche de 100 comme . La variable représente la différence entre le facteur et 100.[6] - Par exemple, .
-
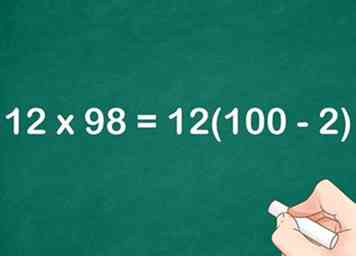 3 Remplacez le facteur ré-exprimé dans l'équation originale. Vous devriez penser à multiplier par le plus petit facteur.
3 Remplacez le facteur ré-exprimé dans l'équation originale. Vous devriez penser à multiplier par le plus petit facteur. - Par exemple, .
-
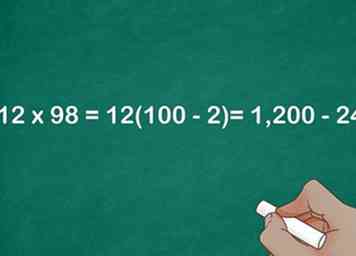 4 Multipliez en utilisant la propriété distributive. Le premier nombre entre parenthèses étant 100, il devrait être facile de trouver le premier facteur. La recherche du deuxième facteur est plus facile, plus le nombre original est proche de 100.
4 Multipliez en utilisant la propriété distributive. Le premier nombre entre parenthèses étant 100, il devrait être facile de trouver le premier facteur. La recherche du deuxième facteur est plus facile, plus le nombre original est proche de 100. - Par exemple, .
-
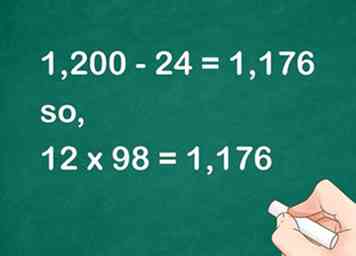 5 Trouvez la différence entre les deux produits. Cela vous donnera le produit de vos deux facteurs originaux.[7]
5 Trouvez la différence entre les deux produits. Cela vous donnera le produit de vos deux facteurs originaux.[7] - Par exemple, , alors .
Méthode trois sur trois:
Doubler et réduire de moitié
-
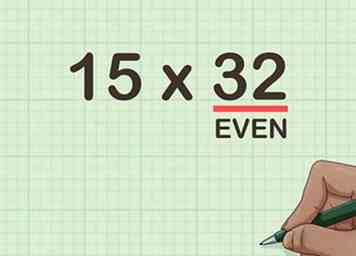 1 Déterminer si l'un ou l'autre facteur est pair. Vous réduirez de moitié le nombre pair.[8] Rappelez-vous qu'un nombre pair est un nombre divisible par 2. Si les deux facteurs sont égaux, choisissez le plus petit nombre à réduire de moitié.
1 Déterminer si l'un ou l'autre facteur est pair. Vous réduirez de moitié le nombre pair.[8] Rappelez-vous qu'un nombre pair est un nombre divisible par 2. Si les deux facteurs sont égaux, choisissez le plus petit nombre à réduire de moitié. - Par exemple, si vous multipliez , vous réduirez de moitié le 32, puisque c'est un nombre pair.
-
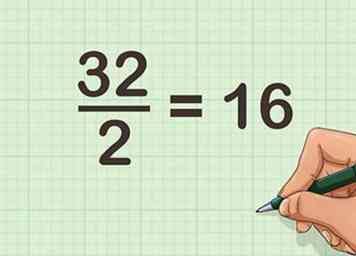 2 La moitié du nombre pair. Pour ce faire, divisez par 2. Si vous connaissez bien vos faits mathématiques, vous devriez pouvoir le faire facilement.
2 La moitié du nombre pair. Pour ce faire, divisez par 2. Si vous connaissez bien vos faits mathématiques, vous devriez pouvoir le faire facilement. - Par exemple, .
-
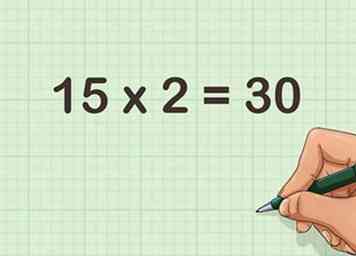 3 Doublez l'autre numéro. Pour doubler un nombre, multipliez-le par 2.
3 Doublez l'autre numéro. Pour doubler un nombre, multipliez-le par 2. - Par exemple, .
-
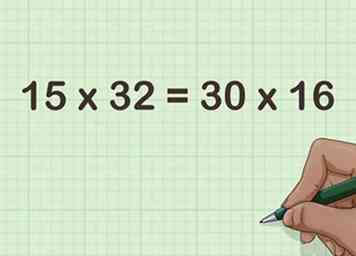 4 Considérons le nouveau problème de multiplication. Le nouveau problème résulte de la réduction de l’un des facteurs et du doublement de l’autre.
4 Considérons le nouveau problème de multiplication. Le nouveau problème résulte de la réduction de l’un des facteurs et du doublement de l’autre. - Par exemple, .
-
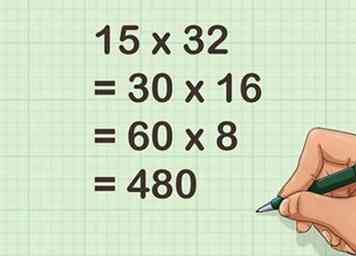 5 Continuez le processus jusqu'à ce que vous arriviez à un problème que vous pouvez calculer mentalement. Assurez-vous de toujours diviser par deux le même nombre et doubler le même nombre. Le nombre de fois que vous divisez par deux et par deux devrait être le même pour les deux facteurs.[9]
5 Continuez le processus jusqu'à ce que vous arriviez à un problème que vous pouvez calculer mentalement. Assurez-vous de toujours diviser par deux le même nombre et doubler le même nombre. Le nombre de fois que vous divisez par deux et par deux devrait être le même pour les deux facteurs.[9] - Par exemple:
- Par exemple:
 Minotauromaquia
Minotauromaquia
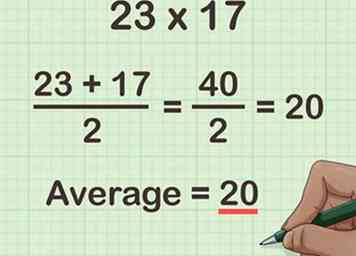 1 Trouvez la moyenne des deux facteurs que vous multipliez. Pour trouver la moyenne, ajoutez les deux nombres ensemble, puis divisez par 2. Vous pouvez également considérer cela comme le nombre dont les deux facteurs sont équidistants.[1]
1 Trouvez la moyenne des deux facteurs que vous multipliez. Pour trouver la moyenne, ajoutez les deux nombres ensemble, puis divisez par 2. Vous pouvez également considérer cela comme le nombre dont les deux facteurs sont équidistants.[1] 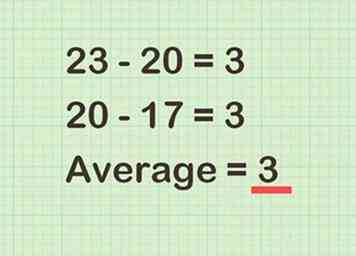 2 Trouvez la différence entre chaque facteur et leur moyenne. Cette différence devrait être la même pour les deux nombres.
2 Trouvez la différence entre chaque facteur et leur moyenne. Cette différence devrait être la même pour les deux nombres. 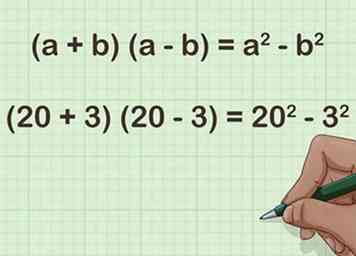 3 Rappelez-vous la formule pour la différence de deux carrés. La formule est
3 Rappelez-vous la formule pour la différence de deux carrés. La formule est 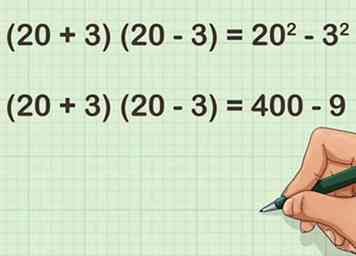 4 Carré
4 Carré 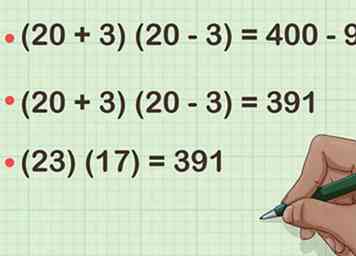 5 Calculez la différence entre les deux carrés. Le résultat sera le produit de vos deux facteurs d'origine.[4]
5 Calculez la différence entre les deux carrés. Le résultat sera le produit de vos deux facteurs d'origine.[4]  1 Déterminer quel facteur est le plus proche de 100. Cette méthode fonctionne mieux lorsque l’un des facteurs est très proche de 100, en particulier si l’un des facteurs est 99.[5]Mais cette méthode peut également fonctionner pour d'autres facteurs.
1 Déterminer quel facteur est le plus proche de 100. Cette méthode fonctionne mieux lorsque l’un des facteurs est très proche de 100, en particulier si l’un des facteurs est 99.[5]Mais cette méthode peut également fonctionner pour d'autres facteurs. 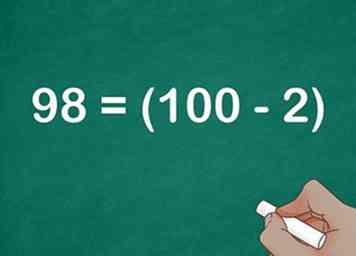 2 Ré-exprimer le facteur le plus proche de 100 comme
2 Ré-exprimer le facteur le plus proche de 100 comme 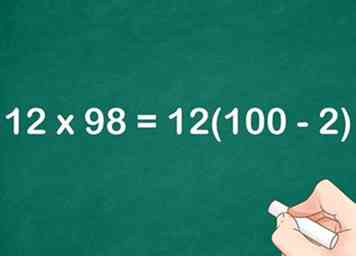 3 Remplacez le facteur ré-exprimé dans l'équation originale. Vous devriez penser à multiplier
3 Remplacez le facteur ré-exprimé dans l'équation originale. Vous devriez penser à multiplier 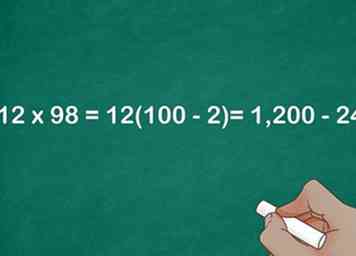 4 Multipliez en utilisant la propriété distributive. Le premier nombre entre parenthèses étant 100, il devrait être facile de trouver le premier facteur. La recherche du deuxième facteur est plus facile, plus le nombre original est proche de 100.
4 Multipliez en utilisant la propriété distributive. Le premier nombre entre parenthèses étant 100, il devrait être facile de trouver le premier facteur. La recherche du deuxième facteur est plus facile, plus le nombre original est proche de 100. 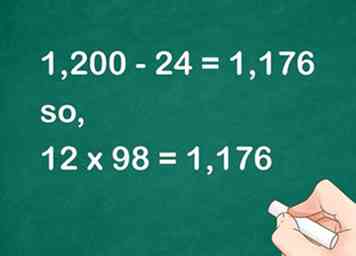 5 Trouvez la différence entre les deux produits. Cela vous donnera le produit de vos deux facteurs originaux.[7]
5 Trouvez la différence entre les deux produits. Cela vous donnera le produit de vos deux facteurs originaux.[7] 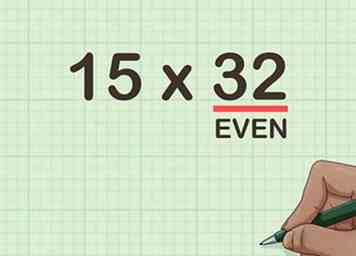 1 Déterminer si l'un ou l'autre facteur est pair. Vous réduirez de moitié le nombre pair.[8] Rappelez-vous qu'un nombre pair est un nombre divisible par 2. Si les deux facteurs sont égaux, choisissez le plus petit nombre à réduire de moitié.
1 Déterminer si l'un ou l'autre facteur est pair. Vous réduirez de moitié le nombre pair.[8] Rappelez-vous qu'un nombre pair est un nombre divisible par 2. Si les deux facteurs sont égaux, choisissez le plus petit nombre à réduire de moitié. 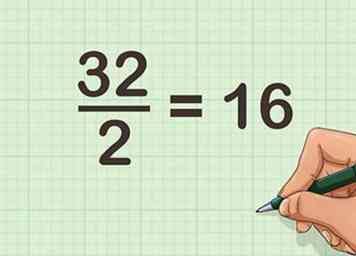 2 La moitié du nombre pair. Pour ce faire, divisez par 2. Si vous connaissez bien vos faits mathématiques, vous devriez pouvoir le faire facilement.
2 La moitié du nombre pair. Pour ce faire, divisez par 2. Si vous connaissez bien vos faits mathématiques, vous devriez pouvoir le faire facilement. 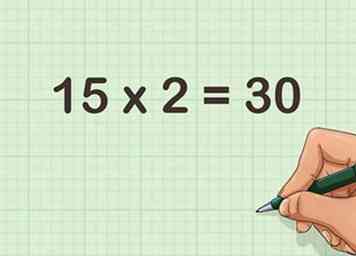 3 Doublez l'autre numéro. Pour doubler un nombre, multipliez-le par 2.
3 Doublez l'autre numéro. Pour doubler un nombre, multipliez-le par 2. 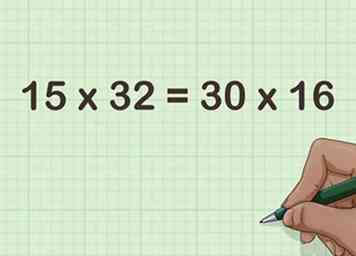 4 Considérons le nouveau problème de multiplication. Le nouveau problème résulte de la réduction de l’un des facteurs et du doublement de l’autre.
4 Considérons le nouveau problème de multiplication. Le nouveau problème résulte de la réduction de l’un des facteurs et du doublement de l’autre. 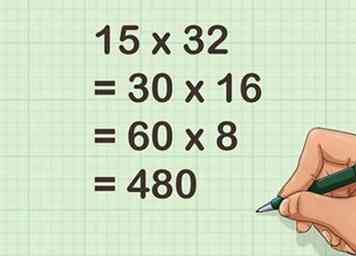 5 Continuez le processus jusqu'à ce que vous arriviez à un problème que vous pouvez calculer mentalement. Assurez-vous de toujours diviser par deux le même nombre et doubler le même nombre. Le nombre de fois que vous divisez par deux et par deux devrait être le même pour les deux facteurs.[9]
5 Continuez le processus jusqu'à ce que vous arriviez à un problème que vous pouvez calculer mentalement. Assurez-vous de toujours diviser par deux le même nombre et doubler le même nombre. Le nombre de fois que vous divisez par deux et par deux devrait être le même pour les deux facteurs.[9]