Il y a plusieurs façons de faire la division. Vous pouvez diviser des nombres décimaux, des fractions ou même des exposants, et vous pouvez faire une division longue ou une division courte. Si vous voulez savoir comment diviser en utilisant plusieurs méthodes, suivez ces étapes.
Méthode One of Five:
Faire la longue division
-
 1 Écrivez le problème. Pour effectuer une division longue, placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division longue, et le dividende, le nombre dans lequel vous le diviserez, dans la barre de division longue.[1]
1 Écrivez le problème. Pour effectuer une division longue, placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division longue, et le dividende, le nombre dans lequel vous le diviserez, dans la barre de division longue.[1] - Ex: 136 ÷ 3
-
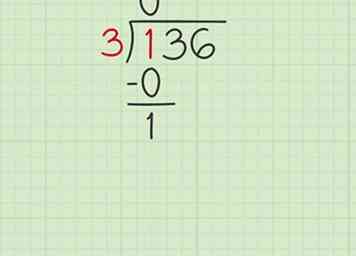 2 Divisez le diviseur en le premier chiffre du premier nombre (si vous le pouvez). Dans ce cas, vous ne pouvez pas diviser 3 en 1, vous devez donc placer un 0 en haut de la barre de division et continuer. Soustrayez 0 de 1 en le plaçant sous le 1 et placez un 1 en dessous car 1-0 = 1.
2 Divisez le diviseur en le premier chiffre du premier nombre (si vous le pouvez). Dans ce cas, vous ne pouvez pas diviser 3 en 1, vous devez donc placer un 0 en haut de la barre de division et continuer. Soustrayez 0 de 1 en le plaçant sous le 1 et placez un 1 en dessous car 1-0 = 1. -
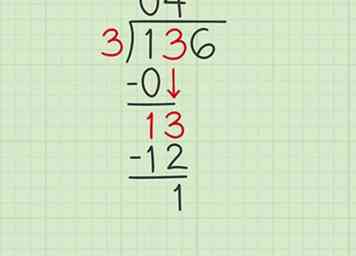 3 Diviser le diviseur dans le nombre qui reste du premier nombre et du deuxième nombre. Comme vous ne pouviez pas diviser 3 en 1, 1 reste. Vous devrez porter le 3 vers le bas. Maintenant, divise 3 en 13. 3 passe en 13 4 fois pour faire 12 avec un reste de 1, alors écris un 4 au-dessus de la longue barre de division, à droite du 0. Ensuite, soustrais 12 de 13 et écris 1 en dessous, puisque 1 est votre reste.
3 Diviser le diviseur dans le nombre qui reste du premier nombre et du deuxième nombre. Comme vous ne pouviez pas diviser 3 en 1, 1 reste. Vous devrez porter le 3 vers le bas. Maintenant, divise 3 en 13. 3 passe en 13 4 fois pour faire 12 avec un reste de 1, alors écris un 4 au-dessus de la longue barre de division, à droite du 0. Ensuite, soustrais 12 de 13 et écris 1 en dessous, puisque 1 est votre reste. -
 4 Diviser le diviseur dans le terme restant. Portez les 6 pour rejoindre le 1, créant 16. Maintenant, divisez 3 en 16. Vous obtiendrez 5 avec un autre reste de 1, car 3 x 5 = 15, et 16-15 est un.
4 Diviser le diviseur dans le terme restant. Portez les 6 pour rejoindre le 1, créant 16. Maintenant, divisez 3 en 16. Vous obtiendrez 5 avec un autre reste de 1, car 3 x 5 = 15, et 16-15 est un. -
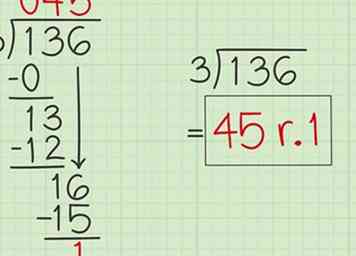 5 Écrivez le reste à côté de votre quotient. Votre réponse finale est 45 avec un reste de 1 ou 45 R1.
5 Écrivez le reste à côté de votre quotient. Votre réponse finale est 45 avec un reste de 1 ou 45 R1.
Méthode deux sur cinq:
Do Short Division
-
 1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Rappelez-vous que si vous voulez faire une division courte, votre diviseur ne peut pas avoir plus d’un chiffre.[2]
1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Rappelez-vous que si vous voulez faire une division courte, votre diviseur ne peut pas avoir plus d’un chiffre.[2] - 518 ÷ 4
-
 2 Divisez votre diviseur en le premier numéro du dividende. 5 ÷ 4 = 1 R1. Placez le quotient, 1, au-dessus de la barre de division longue. Écrivez le reste au-dessus du premier numéro du dividende. Placez un petit 1 au-dessus du 5, pour vous rappeler que vous avez un reste de 1 lorsque vous divisez 5 par 4. 518 devrait maintenant ressembler à ceci: 5118
2 Divisez votre diviseur en le premier numéro du dividende. 5 ÷ 4 = 1 R1. Placez le quotient, 1, au-dessus de la barre de division longue. Écrivez le reste au-dessus du premier numéro du dividende. Placez un petit 1 au-dessus du 5, pour vous rappeler que vous avez un reste de 1 lorsque vous divisez 5 par 4. 518 devrait maintenant ressembler à ceci: 5118 -
 3 Diviser le diviseur par le nombre formé par le reste et le deuxième nombre du dividende. Le chiffre suivant est 11, en utilisant le reste de 1 et le deuxième numéro du dividende. 11 ÷ 4 = 2 R 3, car 4 x 2 = 8 avec 3 restants. Écrivez le reste suivant au-dessus du deuxième numéro du dividende. Placez le 3 au-dessus du 1. Le dividende original, 518, devrait maintenant ressembler à ceci: 51138
3 Diviser le diviseur par le nombre formé par le reste et le deuxième nombre du dividende. Le chiffre suivant est 11, en utilisant le reste de 1 et le deuxième numéro du dividende. 11 ÷ 4 = 2 R 3, car 4 x 2 = 8 avec 3 restants. Écrivez le reste suivant au-dessus du deuxième numéro du dividende. Placez le 3 au-dessus du 1. Le dividende original, 518, devrait maintenant ressembler à ceci: 51138 -
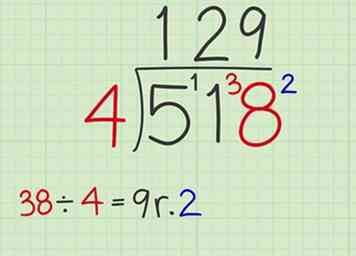 4 Divisez le diviseur par les nombres restants. Le nombre restant est 38 - le reste 3 de l’étape précédente et le chiffre 8 comme dernier terme du dividende. 38 ÷ 4 = 9 R2, parce que 4 x 9 = 36, ce qui est 2 de 38. Écrivez "R2" en haut de la barre de division.
4 Divisez le diviseur par les nombres restants. Le nombre restant est 38 - le reste 3 de l’étape précédente et le chiffre 8 comme dernier terme du dividende. 38 ÷ 4 = 9 R2, parce que 4 x 9 = 36, ce qui est 2 de 38. Écrivez "R2" en haut de la barre de division. -
 5 Indiquez votre réponse finale. Vous pouvez trouver votre réponse finale, le quotient, en haut de la barre de division. C'est 518 ÷ 4 = 129 R2.
5 Indiquez votre réponse finale. Vous pouvez trouver votre réponse finale, le quotient, en haut de la barre de division. C'est 518 ÷ 4 = 129 R2.
Méthode trois sur cinq:
Diviser les fractions
-
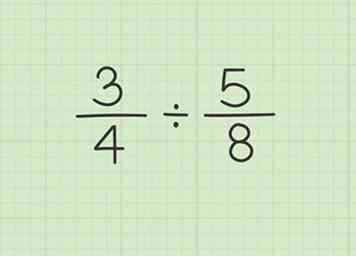 1 Écrivez le problème. Pour diviser les fractions, écrivez simplement la première fraction suivie du symbole de division et de la deuxième fraction.[3]
1 Écrivez le problème. Pour diviser les fractions, écrivez simplement la première fraction suivie du symbole de division et de la deuxième fraction.[3] - Ex: 3/4 ÷ 5/8
-
 2 Inverser le numérateur et le dénominateur de la deuxième fraction. La seconde fraction devient sa propre réciproque.
2 Inverser le numérateur et le dénominateur de la deuxième fraction. La seconde fraction devient sa propre réciproque. - Ex: 3/4 ÷ 8/5
-
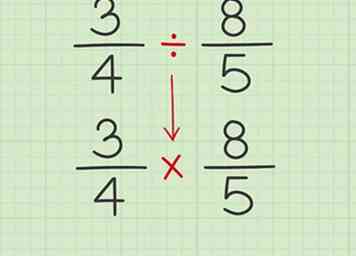 3 Changez le signe de division en un signe de multiplication. Pour diviser les fractions, vous multipliez essentiellement la première fraction par la réciproque du second.
3 Changez le signe de division en un signe de multiplication. Pour diviser les fractions, vous multipliez essentiellement la première fraction par la réciproque du second. - Ex: 3/4 x 8/5
-
 4 Multiplier les numérateurs des fractions. Faites exactement ce que vous feriez pour multiplier deux fractions.
4 Multiplier les numérateurs des fractions. Faites exactement ce que vous feriez pour multiplier deux fractions. - Ex: 3 x 8 = 24
-
 5 Multipliez les dénominateurs des fractions. Terminez le processus de multiplication des deux fractions.
5 Multipliez les dénominateurs des fractions. Terminez le processus de multiplication des deux fractions. - Ex: 4 x 5 = 20
-
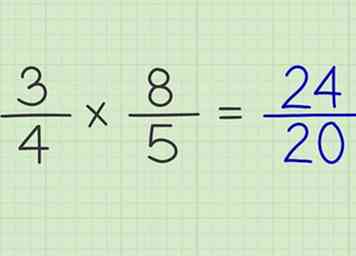 6 Placez le produit des numérateurs sur le produit des dénominateurs. Maintenant que vous avez multiplié les numérateurs et les dénominateurs des deux fractions, vous pouvez former le produit des deux fractions.
6 Placez le produit des numérateurs sur le produit des dénominateurs. Maintenant que vous avez multiplié les numérateurs et les dénominateurs des deux fractions, vous pouvez former le produit des deux fractions. - Ex: 3/4 x 8/5 = 24/20
-
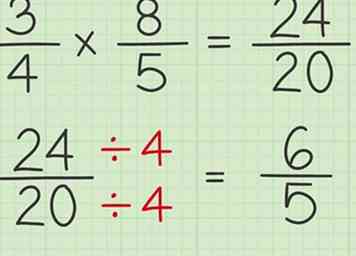 7 Réduisez la fraction. Pour réduire la fraction, trouvez le plus grand facteur commun ou le plus grand nombre qui se divise uniformément dans les deux nombres, puis divisez les deux nombres par ce nombre. Dans le cas de 24 et 20, 4 est le plus grand nombre qui est réparti de manière égale dans les deux nombres. Vous pouvez le confirmer en écrivant tous les facteurs des deux nombres et en entourant le plus grand nombre qui est un facteur des deux:
7 Réduisez la fraction. Pour réduire la fraction, trouvez le plus grand facteur commun ou le plus grand nombre qui se divise uniformément dans les deux nombres, puis divisez les deux nombres par ce nombre. Dans le cas de 24 et 20, 4 est le plus grand nombre qui est réparti de manière égale dans les deux nombres. Vous pouvez le confirmer en écrivant tous les facteurs des deux nombres et en entourant le plus grand nombre qui est un facteur des deux: - 24: 1, 2, 3, 4,6, 8, 12, 24
- 20: 1, 2, 4, 5, 10, 20
- Puisque 4 est le GCF de 24 et 20, il suffit de diviser les deux nombres par 4 pour réduire la fraction.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5
-
 8 Réécrivez la fraction en nombre fractionnaire (facultatif). Pour ce faire, divisez simplement le dénominateur en numérateur et écrivez la réponse en tant que nombre entier. Le reste, ou le nombre qui reste, sera le numérateur de la nouvelle fraction. Le dénominateur de la fraction restera le même. Puisque 5 passe à 6 une fois avec un reste de 1, le nouveau nombre entier est égal à 1 et le nouveau numérateur est égal à 1, créant un nombre mixte de 1 1/5.
8 Réécrivez la fraction en nombre fractionnaire (facultatif). Pour ce faire, divisez simplement le dénominateur en numérateur et écrivez la réponse en tant que nombre entier. Le reste, ou le nombre qui reste, sera le numérateur de la nouvelle fraction. Le dénominateur de la fraction restera le même. Puisque 5 passe à 6 une fois avec un reste de 1, le nouveau nombre entier est égal à 1 et le nouveau numérateur est égal à 1, créant un nombre mixte de 1 1/5. - Ex: 6/5 = 1 1/5
Méthode quatre sur cinq:
Diviser les exposants
-
 1 Assurez-vous que les exposants ont la même base. Vous ne pouvez diviser les nombres avec des exposants que s'ils ont la même base. S'ils n'ont pas la même base, vous devrez les manipuler jusqu'à ce que cela soit possible.[4]
1 Assurez-vous que les exposants ont la même base. Vous ne pouvez diviser les nombres avec des exposants que s'ils ont la même base. S'ils n'ont pas la même base, vous devrez les manipuler jusqu'à ce que cela soit possible.[4] - Ex: x8 ÷ x5
-
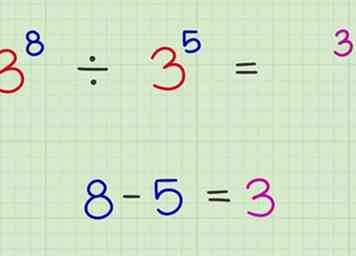 2 Soustraire les exposants. Il suffit de soustraire le deuxième exposant du premier. Ne vous inquiétez pas pour la base pour le moment.
2 Soustraire les exposants. Il suffit de soustraire le deuxième exposant du premier. Ne vous inquiétez pas pour la base pour le moment. - Ex: 8 - 5 = 3
-
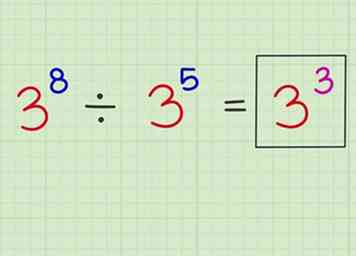 3 Placez le nouvel exposant au-dessus de la base d'origine. Maintenant, vous pouvez écrire le nouvel exposant au-dessus de la base d'origine.
3 Placez le nouvel exposant au-dessus de la base d'origine. Maintenant, vous pouvez écrire le nouvel exposant au-dessus de la base d'origine. - Ex: x8 ÷ x5 = x3
Méthode cinq sur cinq:
Diviser les nombres décimaux
-
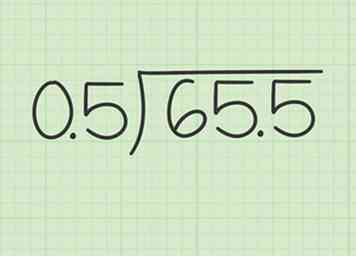 1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Pour diviser les nombres décimaux, votre objectif sera d’abord de convertir les nombres décimaux en nombres entiers.
1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Pour diviser les nombres décimaux, votre objectif sera d’abord de convertir les nombres décimaux en nombres entiers. - Ex: 65,5 5 .5
-
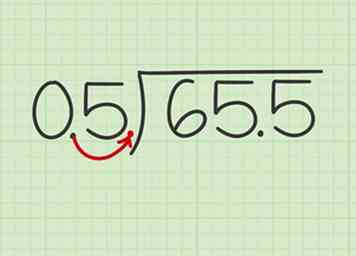 2 Changez le diviseur en un nombre entier. Déplacez simplement le point décimal sur une unité pour changer 0,5 en 5 ou 5,0.
2 Changez le diviseur en un nombre entier. Déplacez simplement le point décimal sur une unité pour changer 0,5 en 5 ou 5,0. -
 3 Changez le dividende en déplaçant son point décimal du même montant. Puisque vous avez déplacé le point décimal de 0,5 sur une unité vers la droite pour en faire un nombre entier, déplacez le point décimal de 65,5 sur une unité vers la droite pour le rendre 655.
3 Changez le dividende en déplaçant son point décimal du même montant. Puisque vous avez déplacé le point décimal de 0,5 sur une unité vers la droite pour en faire un nombre entier, déplacez le point décimal de 65,5 sur une unité vers la droite pour le rendre 655. - Si vous déplacez le point décimal d'un dividende au-delà de tous ses chiffres, vous devez écrire un zéro supplémentaire pour chaque espace déplacé par le point. Par exemple, si vous déplacez le point décimal de 7.2 sur trois espaces, 7.2 devient 7200 car vous avez déplacé le point décimal sur deux espaces vides.
-
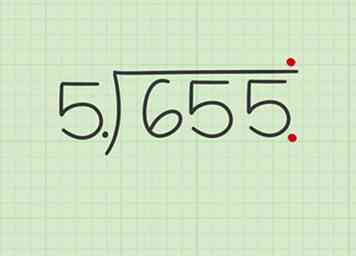 4 Placez un point décimal sur la barre de division longue directement au-dessus de la décimale du dividende. Puisque vous avez déplacé le point décimal sur une seule unité pour obtenir un nombre entier de 0,5, vous devez placer la décimale au-dessus de la barre de division longue à l'endroit où vous avez déplacé le point décimal, juste après les 5 sur 655.
4 Placez un point décimal sur la barre de division longue directement au-dessus de la décimale du dividende. Puisque vous avez déplacé le point décimal sur une seule unité pour obtenir un nombre entier de 0,5, vous devez placer la décimale au-dessus de la barre de division longue à l'endroit où vous avez déplacé le point décimal, juste après les 5 sur 655. -
 5 Résoudre le problème en faisant simple division longue. Pour diviser 5 en 655, procédez comme suit:
5 Résoudre le problème en faisant simple division longue. Pour diviser 5 en 655, procédez comme suit: - Divisez 5 par le chiffre des centièmes, 6. Vous obtenez 1 avec un reste de 1. Placez 1 au centième de la barre de division longue et soustrayez 5 de 6 au-dessous du chiffre six.
- Votre reste, 1, est laissé. Portez les cinq premiers en 655 vers le bas pour créer le numéro 15. Divisez 5 en 15 pour obtenir 3. Placez les trois au-dessus de la barre de division longue, à côté du 1.
- Continuez les 5 dernières. Divisez 5 en 5 pour obtenir 1 et placez le 1 en haut de la barre de division longue. Il n'y a pas de reste puisque 5 va dans 5 également.
- La réponse est le nombre au-dessus de la barre de division longue. 655 ÷ 5 = 131. Notez que c'est aussi la réponse au problème de la division initiale, 65,5 ÷ .5.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Écrivez le problème. Pour effectuer une division longue, placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division longue, et le dividende, le nombre dans lequel vous le diviserez, dans la barre de division longue.[1]
1 Écrivez le problème. Pour effectuer une division longue, placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division longue, et le dividende, le nombre dans lequel vous le diviserez, dans la barre de division longue.[1] 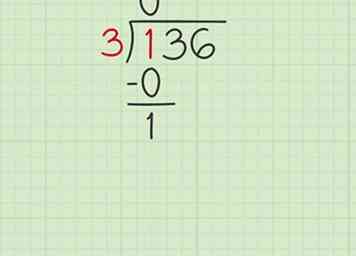 2 Divisez le diviseur en le premier chiffre du premier nombre (si vous le pouvez). Dans ce cas, vous ne pouvez pas diviser 3 en 1, vous devez donc placer un 0 en haut de la barre de division et continuer. Soustrayez 0 de 1 en le plaçant sous le 1 et placez un 1 en dessous car 1-0 = 1.
2 Divisez le diviseur en le premier chiffre du premier nombre (si vous le pouvez). Dans ce cas, vous ne pouvez pas diviser 3 en 1, vous devez donc placer un 0 en haut de la barre de division et continuer. Soustrayez 0 de 1 en le plaçant sous le 1 et placez un 1 en dessous car 1-0 = 1. 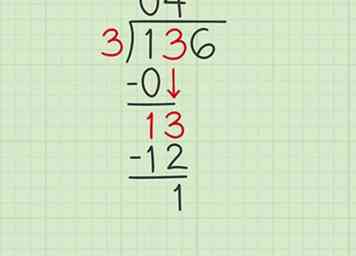 3 Diviser le diviseur dans le nombre qui reste du premier nombre et du deuxième nombre. Comme vous ne pouviez pas diviser 3 en 1, 1 reste. Vous devrez porter le 3 vers le bas. Maintenant, divise 3 en 13. 3 passe en 13 4 fois pour faire 12 avec un reste de 1, alors écris un 4 au-dessus de la longue barre de division, à droite du 0. Ensuite, soustrais 12 de 13 et écris 1 en dessous, puisque 1 est votre reste.
3 Diviser le diviseur dans le nombre qui reste du premier nombre et du deuxième nombre. Comme vous ne pouviez pas diviser 3 en 1, 1 reste. Vous devrez porter le 3 vers le bas. Maintenant, divise 3 en 13. 3 passe en 13 4 fois pour faire 12 avec un reste de 1, alors écris un 4 au-dessus de la longue barre de division, à droite du 0. Ensuite, soustrais 12 de 13 et écris 1 en dessous, puisque 1 est votre reste.  4 Diviser le diviseur dans le terme restant. Portez les 6 pour rejoindre le 1, créant 16. Maintenant, divisez 3 en 16. Vous obtiendrez 5 avec un autre reste de 1, car 3 x 5 = 15, et 16-15 est un.
4 Diviser le diviseur dans le terme restant. Portez les 6 pour rejoindre le 1, créant 16. Maintenant, divisez 3 en 16. Vous obtiendrez 5 avec un autre reste de 1, car 3 x 5 = 15, et 16-15 est un. 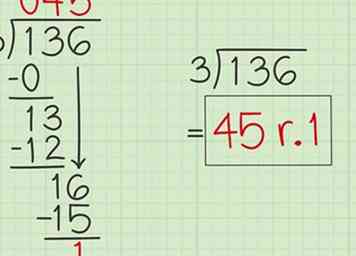 5 Écrivez le reste à côté de votre quotient. Votre réponse finale est 45 avec un reste de 1 ou 45 R1.
5 Écrivez le reste à côté de votre quotient. Votre réponse finale est 45 avec un reste de 1 ou 45 R1.  1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Rappelez-vous que si vous voulez faire une division courte, votre diviseur ne peut pas avoir plus d’un chiffre.[2]
1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Rappelez-vous que si vous voulez faire une division courte, votre diviseur ne peut pas avoir plus d’un chiffre.[2]  2 Divisez votre diviseur en le premier numéro du dividende. 5 ÷ 4 = 1 R1. Placez le quotient, 1, au-dessus de la barre de division longue. Écrivez le reste au-dessus du premier numéro du dividende. Placez un petit 1 au-dessus du 5, pour vous rappeler que vous avez un reste de 1 lorsque vous divisez 5 par 4. 518 devrait maintenant ressembler à ceci: 5118
2 Divisez votre diviseur en le premier numéro du dividende. 5 ÷ 4 = 1 R1. Placez le quotient, 1, au-dessus de la barre de division longue. Écrivez le reste au-dessus du premier numéro du dividende. Placez un petit 1 au-dessus du 5, pour vous rappeler que vous avez un reste de 1 lorsque vous divisez 5 par 4. 518 devrait maintenant ressembler à ceci: 5118  3 Diviser le diviseur par le nombre formé par le reste et le deuxième nombre du dividende. Le chiffre suivant est 11, en utilisant le reste de 1 et le deuxième numéro du dividende. 11 ÷ 4 = 2 R 3, car 4 x 2 = 8 avec 3 restants. Écrivez le reste suivant au-dessus du deuxième numéro du dividende. Placez le 3 au-dessus du 1. Le dividende original, 518, devrait maintenant ressembler à ceci: 51138
3 Diviser le diviseur par le nombre formé par le reste et le deuxième nombre du dividende. Le chiffre suivant est 11, en utilisant le reste de 1 et le deuxième numéro du dividende. 11 ÷ 4 = 2 R 3, car 4 x 2 = 8 avec 3 restants. Écrivez le reste suivant au-dessus du deuxième numéro du dividende. Placez le 3 au-dessus du 1. Le dividende original, 518, devrait maintenant ressembler à ceci: 51138 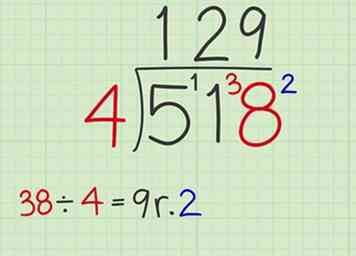 4 Divisez le diviseur par les nombres restants. Le nombre restant est 38 - le reste 3 de l’étape précédente et le chiffre 8 comme dernier terme du dividende. 38 ÷ 4 = 9 R2, parce que 4 x 9 = 36, ce qui est 2 de 38. Écrivez "R2" en haut de la barre de division.
4 Divisez le diviseur par les nombres restants. Le nombre restant est 38 - le reste 3 de l’étape précédente et le chiffre 8 comme dernier terme du dividende. 38 ÷ 4 = 9 R2, parce que 4 x 9 = 36, ce qui est 2 de 38. Écrivez "R2" en haut de la barre de division.  5 Indiquez votre réponse finale. Vous pouvez trouver votre réponse finale, le quotient, en haut de la barre de division. C'est 518 ÷ 4 = 129 R2.
5 Indiquez votre réponse finale. Vous pouvez trouver votre réponse finale, le quotient, en haut de la barre de division. C'est 518 ÷ 4 = 129 R2. 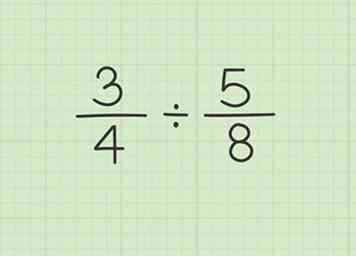 1 Écrivez le problème. Pour diviser les fractions, écrivez simplement la première fraction suivie du symbole de division et de la deuxième fraction.[3]
1 Écrivez le problème. Pour diviser les fractions, écrivez simplement la première fraction suivie du symbole de division et de la deuxième fraction.[3]  2 Inverser le numérateur et le dénominateur de la deuxième fraction. La seconde fraction devient sa propre réciproque.
2 Inverser le numérateur et le dénominateur de la deuxième fraction. La seconde fraction devient sa propre réciproque. 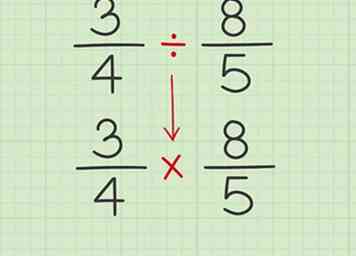 3 Changez le signe de division en un signe de multiplication. Pour diviser les fractions, vous multipliez essentiellement la première fraction par la réciproque du second.
3 Changez le signe de division en un signe de multiplication. Pour diviser les fractions, vous multipliez essentiellement la première fraction par la réciproque du second.  4 Multiplier les numérateurs des fractions. Faites exactement ce que vous feriez pour multiplier deux fractions.
4 Multiplier les numérateurs des fractions. Faites exactement ce que vous feriez pour multiplier deux fractions.  5 Multipliez les dénominateurs des fractions. Terminez le processus de multiplication des deux fractions.
5 Multipliez les dénominateurs des fractions. Terminez le processus de multiplication des deux fractions. 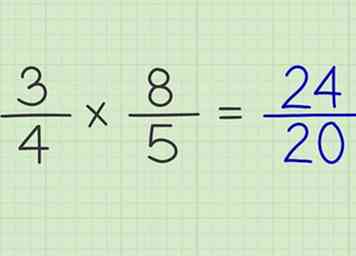 6 Placez le produit des numérateurs sur le produit des dénominateurs. Maintenant que vous avez multiplié les numérateurs et les dénominateurs des deux fractions, vous pouvez former le produit des deux fractions.
6 Placez le produit des numérateurs sur le produit des dénominateurs. Maintenant que vous avez multiplié les numérateurs et les dénominateurs des deux fractions, vous pouvez former le produit des deux fractions. 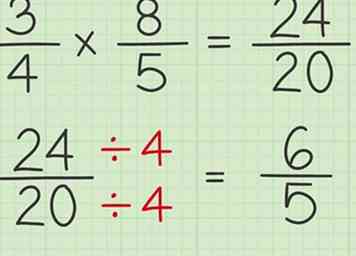 7 Réduisez la fraction. Pour réduire la fraction, trouvez le plus grand facteur commun ou le plus grand nombre qui se divise uniformément dans les deux nombres, puis divisez les deux nombres par ce nombre. Dans le cas de 24 et 20, 4 est le plus grand nombre qui est réparti de manière égale dans les deux nombres. Vous pouvez le confirmer en écrivant tous les facteurs des deux nombres et en entourant le plus grand nombre qui est un facteur des deux:
7 Réduisez la fraction. Pour réduire la fraction, trouvez le plus grand facteur commun ou le plus grand nombre qui se divise uniformément dans les deux nombres, puis divisez les deux nombres par ce nombre. Dans le cas de 24 et 20, 4 est le plus grand nombre qui est réparti de manière égale dans les deux nombres. Vous pouvez le confirmer en écrivant tous les facteurs des deux nombres et en entourant le plus grand nombre qui est un facteur des deux:  8 Réécrivez la fraction en nombre fractionnaire (facultatif). Pour ce faire, divisez simplement le dénominateur en numérateur et écrivez la réponse en tant que nombre entier. Le reste, ou le nombre qui reste, sera le numérateur de la nouvelle fraction. Le dénominateur de la fraction restera le même. Puisque 5 passe à 6 une fois avec un reste de 1, le nouveau nombre entier est égal à 1 et le nouveau numérateur est égal à 1, créant un nombre mixte de 1 1/5.
8 Réécrivez la fraction en nombre fractionnaire (facultatif). Pour ce faire, divisez simplement le dénominateur en numérateur et écrivez la réponse en tant que nombre entier. Le reste, ou le nombre qui reste, sera le numérateur de la nouvelle fraction. Le dénominateur de la fraction restera le même. Puisque 5 passe à 6 une fois avec un reste de 1, le nouveau nombre entier est égal à 1 et le nouveau numérateur est égal à 1, créant un nombre mixte de 1 1/5.  1 Assurez-vous que les exposants ont la même base. Vous ne pouvez diviser les nombres avec des exposants que s'ils ont la même base. S'ils n'ont pas la même base, vous devrez les manipuler jusqu'à ce que cela soit possible.[4]
1 Assurez-vous que les exposants ont la même base. Vous ne pouvez diviser les nombres avec des exposants que s'ils ont la même base. S'ils n'ont pas la même base, vous devrez les manipuler jusqu'à ce que cela soit possible.[4] 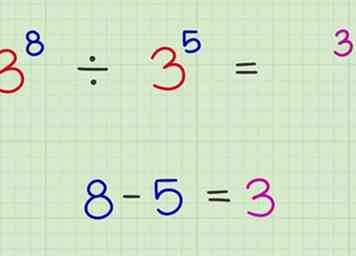 2 Soustraire les exposants. Il suffit de soustraire le deuxième exposant du premier. Ne vous inquiétez pas pour la base pour le moment.
2 Soustraire les exposants. Il suffit de soustraire le deuxième exposant du premier. Ne vous inquiétez pas pour la base pour le moment.  3 Placez le nouvel exposant au-dessus de la base d'origine. Maintenant, vous pouvez écrire le nouvel exposant au-dessus de la base d'origine.
3 Placez le nouvel exposant au-dessus de la base d'origine. Maintenant, vous pouvez écrire le nouvel exposant au-dessus de la base d'origine. 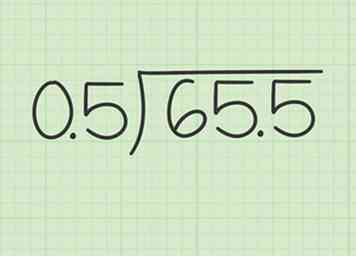 1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Pour diviser les nombres décimaux, votre objectif sera d’abord de convertir les nombres décimaux en nombres entiers.
1 Écrivez le problème. Placez le diviseur, le nombre que vous diviserez, en dehors de la barre de division et le dividende, le nombre dans lequel vous le diviserez, à l'intérieur de la barre de division. Pour diviser les nombres décimaux, votre objectif sera d’abord de convertir les nombres décimaux en nombres entiers. 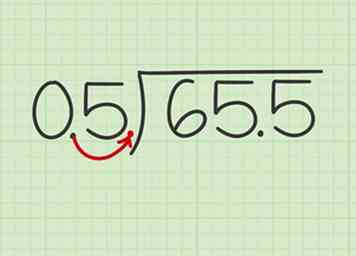 2 Changez le diviseur en un nombre entier. Déplacez simplement le point décimal sur une unité pour changer 0,5 en 5 ou 5,0.
2 Changez le diviseur en un nombre entier. Déplacez simplement le point décimal sur une unité pour changer 0,5 en 5 ou 5,0.  3 Changez le dividende en déplaçant son point décimal du même montant. Puisque vous avez déplacé le point décimal de 0,5 sur une unité vers la droite pour en faire un nombre entier, déplacez le point décimal de 65,5 sur une unité vers la droite pour le rendre 655.
3 Changez le dividende en déplaçant son point décimal du même montant. Puisque vous avez déplacé le point décimal de 0,5 sur une unité vers la droite pour en faire un nombre entier, déplacez le point décimal de 65,5 sur une unité vers la droite pour le rendre 655. 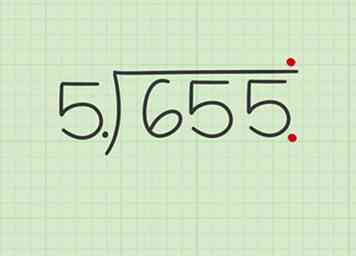 4 Placez un point décimal sur la barre de division longue directement au-dessus de la décimale du dividende. Puisque vous avez déplacé le point décimal sur une seule unité pour obtenir un nombre entier de 0,5, vous devez placer la décimale au-dessus de la barre de division longue à l'endroit où vous avez déplacé le point décimal, juste après les 5 sur 655.
4 Placez un point décimal sur la barre de division longue directement au-dessus de la décimale du dividende. Puisque vous avez déplacé le point décimal sur une seule unité pour obtenir un nombre entier de 0,5, vous devez placer la décimale au-dessus de la barre de division longue à l'endroit où vous avez déplacé le point décimal, juste après les 5 sur 655.  5 Résoudre le problème en faisant simple division longue. Pour diviser 5 en 655, procédez comme suit:
5 Résoudre le problème en faisant simple division longue. Pour diviser 5 en 655, procédez comme suit: