Les problèmes de division binaire peuvent être résolus en utilisant la division longue, qui est une méthode utile pour vous enseigner le processus ou pour écrire un programme informatique simple. Alternativement, la méthode de complément de soustraction répétée fournit une approche que vous ne connaissez peut-être pas bien qu'elle ne soit pas aussi couramment utilisée en programmation.[1] Les langages machine utilisent généralement un algorithme d'estimation pour une plus grande efficacité, mais ils ne sont pas décrits ici.[2]
Méthode One of Two:
Utilisation de la division longue
-
 1 Révisez la division décimale longue. Si cela fait un moment que vous avez fait une division longue avec des nombres décimaux ordinaires (base dix), passez en revue les bases en utilisant le problème 4. Sinon, passez directement à l'étape suivante pour apprendre le même processus en binaire.
1 Révisez la division décimale longue. Si cela fait un moment que vous avez fait une division longue avec des nombres décimaux ordinaires (base dix), passez en revue les bases en utilisant le problème 4. Sinon, passez directement à l'étape suivante pour apprendre le même processus en binaire. - le dividende est divisé par le diviseur, et la réponse est la quotient.
- Comparez le diviseur au premier chiffre du dividende. Si le diviseur est le plus grand nombre, continuez à ajouter des chiffres au dividende jusqu'à ce que le diviseur soit le plus petit nombre. (Par exemple, si vous calculez 172 ÷ 4, nous comparerions 4 et 1, notez que 4> 1 et comparez plutôt 4 à 17).
- Écrivez le premier chiffre du quotient au-dessus du dernier chiffre de dividende que vous utilisiez dans la comparaison. En comparant 4 et 17, nous voyons que 4 entre dans 17 quatre fois, donc nous écrivons 4 comme premier chiffre de notre quotient, au-dessus du 7.
- Multipliez et soustrayez pour trouver le reste. Multipliez le chiffre du quotient par le diviseur, dans ce cas 4 x 4 = 16. Écrivez les 16 sous le 17, puis soustrayez 17 - 16 pour trouver le reste, 1.
- Répéter. Encore une fois, nous comparons le diviseur 4 avec le chiffre suivant, 1, notons que 4> 1 et "abaissons" le chiffre suivant du dividende, pour comparer 4 à 12 à la place. 4 va dans 12 trois fois sans reste, donc nous écrivons 3 comme chiffre suivant du quotient. La réponse est 43.
-
 2 Configurez le problème de division longue binaire. Prenons l'exemple 10101 ÷ 11. Écris ceci comme un problème de longue division, avec le 10101 comme dividende et le 11 comme diviseur. Laissez un espace au-dessus pour écrire le quotient et ci-dessous pour écrire vos calculs.
2 Configurez le problème de division longue binaire. Prenons l'exemple 10101 ÷ 11. Écris ceci comme un problème de longue division, avec le 10101 comme dividende et le 11 comme diviseur. Laissez un espace au-dessus pour écrire le quotient et ci-dessous pour écrire vos calculs. -
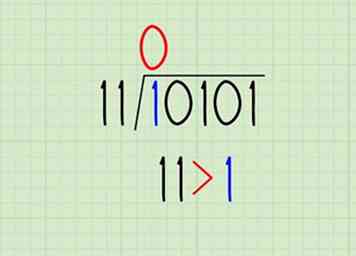 3 Comparez le diviseur au premier chiffre du dividende. Cela fonctionne comme un problème décimal de division longue, mais en fait, c'est un peu plus facile en binaire. Soit vous ne pouvez pas diviser le nombre par le diviseur (0) ou le diviseur peut aller en une seule fois (1):
3 Comparez le diviseur au premier chiffre du dividende. Cela fonctionne comme un problème décimal de division longue, mais en fait, c'est un peu plus facile en binaire. Soit vous ne pouvez pas diviser le nombre par le diviseur (0) ou le diviseur peut aller en une seule fois (1): - 11> 1, donc 11 ne peut pas "entrer" 1. Écrivez un 0 comme premier chiffre du quotient (au-dessus du premier chiffre du dividende).
-
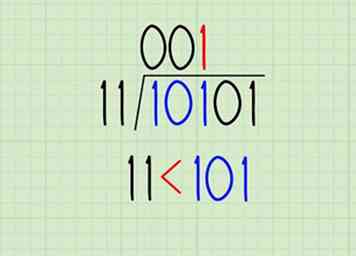 4 Taper sur le chiffre suivant et répéter jusqu'à obtenir un 1. Voici les prochaines étapes de notre exemple:
4 Taper sur le chiffre suivant et répéter jusqu'à obtenir un 1. Voici les prochaines étapes de notre exemple: - Abaissez le prochain chiffre du dividende. 11> 10. Écrivez un 0 dans le quotient.
- Abaissez le chiffre suivant. 11 <101. Écrivez un 1 dans le quotient.
-
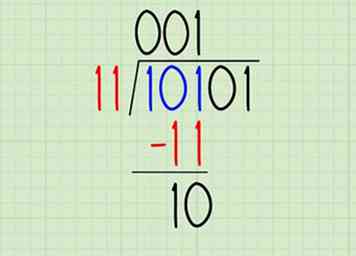 5 Trouvez le reste. Comme dans la division décimale longue, nous multiplions le chiffre que nous venons de trouver (1) par le diviseur (11) et inscrivons le résultat sous notre dividende aligné sur le chiffre que nous venons de calculer. En binaire, on peut raccourcir ceci, puisque 1 x le diviseur est toujours égal au diviseur:
5 Trouvez le reste. Comme dans la division décimale longue, nous multiplions le chiffre que nous venons de trouver (1) par le diviseur (11) et inscrivons le résultat sous notre dividende aligné sur le chiffre que nous venons de calculer. En binaire, on peut raccourcir ceci, puisque 1 x le diviseur est toujours égal au diviseur: - Écrivez le diviseur sous le dividende. Ici, nous écrivons 11 alignés sous les trois premiers chiffres (101) du dividende.
- Calculez 101 - 11 pour obtenir le reste, 10. Découvrez comment soustraire des nombres binaires si vous avez besoin d'une révision.
-
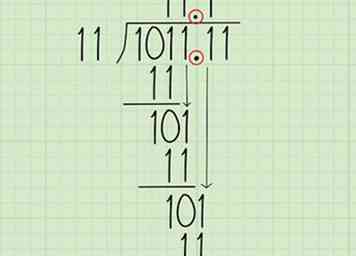
 6 Répétez jusqu'à ce que le problème soit fini. Ramenez le chiffre suivant du diviseur au reste pour faire 100. Depuis 11 <100, écrivez un 1 comme prochain chiffre du quotient. Continuer le problème comme avant:
6 Répétez jusqu'à ce que le problème soit fini. Ramenez le chiffre suivant du diviseur au reste pour faire 100. Depuis 11 <100, écrivez un 1 comme prochain chiffre du quotient. Continuer le problème comme avant: - Écrivez 11 sous le 100 et soustrayez pour obtenir 1.
- Abaisser le dernier chiffre du dividende pour faire 11.
- 11 = 11, écrivez donc un 1 comme dernier chiffre du quotient (la réponse).
- Il n'y a pas de reste, le problème est donc complet. La réponse est 00111, ou simplement 111.
-
 7 Ajoutez un point de radix si nécessaire. Parfois, le résultat n'est pas un entier. Si vous avez encore un reste après avoir utilisé le dernier chiffre, ajoutez un ".0" au dividende et un "." à votre quotient, de sorte que vous pouvez faire un autre chiffre et continuer. Répétez jusqu'à atteindre la spécificité souhaitée, puis arrondissez la réponse. Sur du papier, vous pouvez arrondir le chiffre inférieur en coupant le dernier 0, ou si le dernier chiffre est un 1, déposez-le et ajoutez 1 au dernier dernier chiffre. En programmation, suivez l’un des algorithmes standard d’arrondi pour éviter les erreurs lors de la conversion entre les nombres binaires et décimaux.[3]
7 Ajoutez un point de radix si nécessaire. Parfois, le résultat n'est pas un entier. Si vous avez encore un reste après avoir utilisé le dernier chiffre, ajoutez un ".0" au dividende et un "." à votre quotient, de sorte que vous pouvez faire un autre chiffre et continuer. Répétez jusqu'à atteindre la spécificité souhaitée, puis arrondissez la réponse. Sur du papier, vous pouvez arrondir le chiffre inférieur en coupant le dernier 0, ou si le dernier chiffre est un 1, déposez-le et ajoutez 1 au dernier dernier chiffre. En programmation, suivez l’un des algorithmes standard d’arrondi pour éviter les erreurs lors de la conversion entre les nombres binaires et décimaux.[3] - Les problèmes de division binaire se terminent souvent par la répétition de parties fractionnaires, plus souvent qu'elles ne le sont en notation décimale.[4]
- Ceci est appelé le terme plus général "point de base", qui s'applique dans n'importe quelle base, puisque le "point décimal" est utilisé uniquement dans le système décimal.[5]
Méthode deux sur deux:
Utiliser la méthode du complément
-
 1 Comprendre le concept de base. Une façon de résoudre les problèmes de division - dans n'importe quelle base - est de continuer à soustraire le diviseur du dividende, puis le reste, tout en calculant le nombre de fois que vous pouvez le faire avant d'obtenir un nombre négatif. Voici un exemple dans la base dix, résolvant le problème 26 ÷ 7:
1 Comprendre le concept de base. Une façon de résoudre les problèmes de division - dans n'importe quelle base - est de continuer à soustraire le diviseur du dividende, puis le reste, tout en calculant le nombre de fois que vous pouvez le faire avant d'obtenir un nombre négatif. Voici un exemple dans la base dix, résolvant le problème 26 ÷ 7: - 26 - 7 = 19 (soustrait 1 temps)
- 19 - 7 = 12 (2)
- 12 - 7 = 5 (3)
- 5 - 7 = -2. Nombre négatif, donc sauvegarder. La réponse est 3 avec un reste de 5. Notez que cette méthode ne calcule aucune partie non entière de la réponse.
-
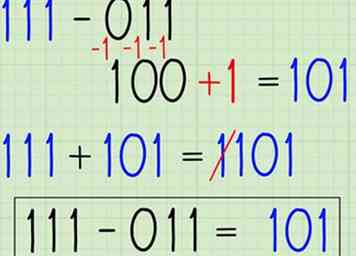 2 Apprenez à soustraire par des compléments. Bien que vous puissiez facilement utiliser la méthode ci-dessus en binaire, nous pouvons également soustraire par une méthode plus efficace, ce qui permet de gagner du temps lors de la programmation des ordinateurs pour diviser des nombres binaires. C'est la méthode de soustraction par compléments en binaire. Voici les bases, en calculant 111 - 011 (assurez-vous que les deux nombres ont la même longueur):
2 Apprenez à soustraire par des compléments. Bien que vous puissiez facilement utiliser la méthode ci-dessus en binaire, nous pouvons également soustraire par une méthode plus efficace, ce qui permet de gagner du temps lors de la programmation des ordinateurs pour diviser des nombres binaires. C'est la méthode de soustraction par compléments en binaire. Voici les bases, en calculant 111 - 011 (assurez-vous que les deux nombres ont la même longueur): - Trouvez le complément du deuxième terme, en soustrayant chaque chiffre de 1.Cela se fait facilement en binaire en basculant chaque 1 sur 0 et chaque 0 sur 1.[6][7] Dans notre exemple, 011 devient 100.
- Ajoutez-en un au résultat: 100 + 1 = 101. Ceci s'appelle le complément à deux, et nous permet d'effectuer une soustraction en tant que problème d'addition.[8] Essentiellement, le résultat est comme si nous avions ajouté un nombre négatif au lieu de soustraire un nombre positif, une fois le processus terminé.
- Ajoutez le résultat au premier terme. Écrivez et résolvez le problème d'addition: 111 + 101 = 1100.
- Jeter le chiffre de transport. Jeter le premier chiffre de votre réponse pour obtenir le résultat final. 1100 → 100.
-
 3 Combinez les deux concepts ci-dessus. Vous connaissez maintenant la méthode de soustraction des problèmes de division et la méthode du complément à deux pour résoudre les problèmes de soustraction. Vous pouvez combiner ceci en une seule méthode pour résoudre les problèmes de division, en utilisant les étapes ci-dessous.[9] Si vous le souhaitez, vous pouvez essayer de le comprendre vous-même avant de continuer.
3 Combinez les deux concepts ci-dessus. Vous connaissez maintenant la méthode de soustraction des problèmes de division et la méthode du complément à deux pour résoudre les problèmes de soustraction. Vous pouvez combiner ceci en une seule méthode pour résoudre les problèmes de division, en utilisant les étapes ci-dessous.[9] Si vous le souhaitez, vous pouvez essayer de le comprendre vous-même avant de continuer. -
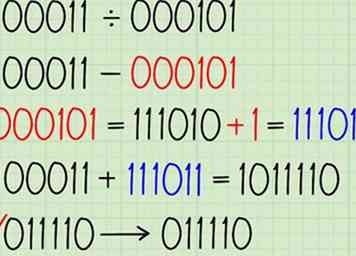 4 Soustrayez le diviseur du dividende en ajoutant deux compléments. Passons en revue le problème 100011 ÷ 000101. La première étape consiste à résoudre le problème 100011 - 000101, en utilisant la méthode du complément twos pour en faire un problème supplémentaire:
4 Soustrayez le diviseur du dividende en ajoutant deux compléments. Passons en revue le problème 100011 ÷ 000101. La première étape consiste à résoudre le problème 100011 - 000101, en utilisant la méthode du complément twos pour en faire un problème supplémentaire: - Complément Twos de 000101 = 111010 + 1 = 111011
- 100011 + 111011 = 1011110
- Jetez le bit de retenue → 011110
-
 5 Ajoutez-en un au quotient. Dans un programme informatique, c'est le point où vous incrémentez le quotient de un. Sur papier, faites une note quelque part dans un coin où elle ne sera pas confondue avec votre autre travail. Nous avons soustrait une fois avec succès, donc le quotient jusqu'à présent est 1.
5 Ajoutez-en un au quotient. Dans un programme informatique, c'est le point où vous incrémentez le quotient de un. Sur papier, faites une note quelque part dans un coin où elle ne sera pas confondue avec votre autre travail. Nous avons soustrait une fois avec succès, donc le quotient jusqu'à présent est 1. -
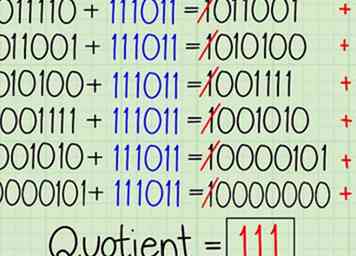 6 Répétez en soustrayant le diviseur du reste. Le résultat de notre dernier calcul est le reste qui reste après que le diviseur "est entré" une fois. Continuez à ajouter le complément à deux du diviseur à chaque fois et supprimez le bit de retenue. Ajoutez-en un au quotient à chaque fois, en répétant jusqu'à ce que vous obteniez un reste égal ou inférieur à votre diviseur:[10]
6 Répétez en soustrayant le diviseur du reste. Le résultat de notre dernier calcul est le reste qui reste après que le diviseur "est entré" une fois. Continuez à ajouter le complément à deux du diviseur à chaque fois et supprimez le bit de retenue. Ajoutez-en un au quotient à chaque fois, en répétant jusqu'à ce que vous obteniez un reste égal ou inférieur à votre diviseur:[10] - 011110 + 111011 = 1011001 → 011001 (quotient 1+1=10)
- 011001 + 111011 = 1010100 → 010100 (quotient 10+1=11)
- 010100 + 111011 = 1001111 → 001111 (11+1=100)
- 001111 + 111011 = 1001010 → 001010 (100+1=101)
- 001010 + 111011 = 10000101 → 0000101 (101+1=110)
- 0000101 + 111011 = 1000000 → 000000 (110+1=111)
- 0 est plus petit que 101, donc nous nous arrêtons ici. Le quotient 111 est la réponse au problème de la division. Le reste est le résultat final de notre problème de soustraction, dans ce cas 0 (pas de reste).
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Révisez la division décimale longue. Si cela fait un moment que vous avez fait une division longue avec des nombres décimaux ordinaires (base dix), passez en revue les bases en utilisant le problème 4. Sinon, passez directement à l'étape suivante pour apprendre le même processus en binaire.
1 Révisez la division décimale longue. Si cela fait un moment que vous avez fait une division longue avec des nombres décimaux ordinaires (base dix), passez en revue les bases en utilisant le problème 4. Sinon, passez directement à l'étape suivante pour apprendre le même processus en binaire.  2 Configurez le problème de division longue binaire. Prenons l'exemple 10101 ÷ 11. Écris ceci comme un problème de longue division, avec le 10101 comme dividende et le 11 comme diviseur. Laissez un espace au-dessus pour écrire le quotient et ci-dessous pour écrire vos calculs.
2 Configurez le problème de division longue binaire. Prenons l'exemple 10101 ÷ 11. Écris ceci comme un problème de longue division, avec le 10101 comme dividende et le 11 comme diviseur. Laissez un espace au-dessus pour écrire le quotient et ci-dessous pour écrire vos calculs. 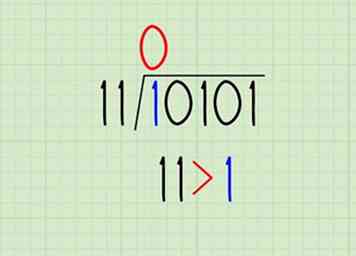 3 Comparez le diviseur au premier chiffre du dividende. Cela fonctionne comme un problème décimal de division longue, mais en fait, c'est un peu plus facile en binaire. Soit vous ne pouvez pas diviser le nombre par le diviseur (0) ou le diviseur peut aller en une seule fois (1):
3 Comparez le diviseur au premier chiffre du dividende. Cela fonctionne comme un problème décimal de division longue, mais en fait, c'est un peu plus facile en binaire. Soit vous ne pouvez pas diviser le nombre par le diviseur (0) ou le diviseur peut aller en une seule fois (1): 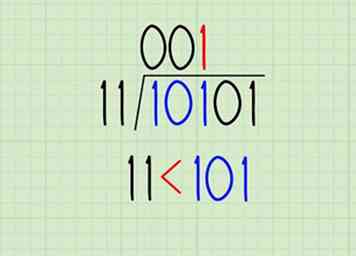 4 Taper sur le chiffre suivant et répéter jusqu'à obtenir un 1. Voici les prochaines étapes de notre exemple:
4 Taper sur le chiffre suivant et répéter jusqu'à obtenir un 1. Voici les prochaines étapes de notre exemple: 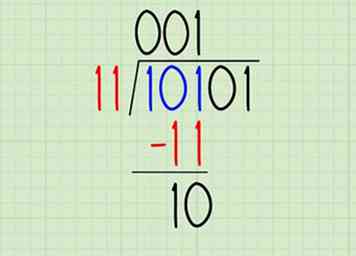 5 Trouvez le reste. Comme dans la division décimale longue, nous multiplions le chiffre que nous venons de trouver (1) par le diviseur (11) et inscrivons le résultat sous notre dividende aligné sur le chiffre que nous venons de calculer. En binaire, on peut raccourcir ceci, puisque 1 x le diviseur est toujours égal au diviseur:
5 Trouvez le reste. Comme dans la division décimale longue, nous multiplions le chiffre que nous venons de trouver (1) par le diviseur (11) et inscrivons le résultat sous notre dividende aligné sur le chiffre que nous venons de calculer. En binaire, on peut raccourcir ceci, puisque 1 x le diviseur est toujours égal au diviseur:  6 Répétez jusqu'à ce que le problème soit fini. Ramenez le chiffre suivant du diviseur au reste pour faire 100. Depuis 11 <100, écrivez un 1 comme prochain chiffre du quotient. Continuer le problème comme avant:
6 Répétez jusqu'à ce que le problème soit fini. Ramenez le chiffre suivant du diviseur au reste pour faire 100. Depuis 11 <100, écrivez un 1 comme prochain chiffre du quotient. Continuer le problème comme avant:  7 Ajoutez un point de radix si nécessaire. Parfois, le résultat n'est pas un entier. Si vous avez encore un reste après avoir utilisé le dernier chiffre, ajoutez un ".0" au dividende et un "." à votre quotient, de sorte que vous pouvez faire un autre chiffre et continuer. Répétez jusqu'à atteindre la spécificité souhaitée, puis arrondissez la réponse. Sur du papier, vous pouvez arrondir le chiffre inférieur en coupant le dernier 0, ou si le dernier chiffre est un 1, déposez-le et ajoutez 1 au dernier dernier chiffre. En programmation, suivez l’un des algorithmes standard d’arrondi pour éviter les erreurs lors de la conversion entre les nombres binaires et décimaux.[3]
7 Ajoutez un point de radix si nécessaire. Parfois, le résultat n'est pas un entier. Si vous avez encore un reste après avoir utilisé le dernier chiffre, ajoutez un ".0" au dividende et un "." à votre quotient, de sorte que vous pouvez faire un autre chiffre et continuer. Répétez jusqu'à atteindre la spécificité souhaitée, puis arrondissez la réponse. Sur du papier, vous pouvez arrondir le chiffre inférieur en coupant le dernier 0, ou si le dernier chiffre est un 1, déposez-le et ajoutez 1 au dernier dernier chiffre. En programmation, suivez l’un des algorithmes standard d’arrondi pour éviter les erreurs lors de la conversion entre les nombres binaires et décimaux.[3]  1 Comprendre le concept de base. Une façon de résoudre les problèmes de division - dans n'importe quelle base - est de continuer à soustraire le diviseur du dividende, puis le reste, tout en calculant le nombre de fois que vous pouvez le faire avant d'obtenir un nombre négatif. Voici un exemple dans la base dix, résolvant le problème 26 ÷ 7:
1 Comprendre le concept de base. Une façon de résoudre les problèmes de division - dans n'importe quelle base - est de continuer à soustraire le diviseur du dividende, puis le reste, tout en calculant le nombre de fois que vous pouvez le faire avant d'obtenir un nombre négatif. Voici un exemple dans la base dix, résolvant le problème 26 ÷ 7: 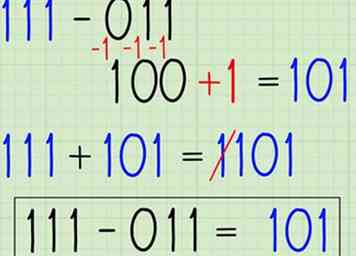 2 Apprenez à soustraire par des compléments. Bien que vous puissiez facilement utiliser la méthode ci-dessus en binaire, nous pouvons également soustraire par une méthode plus efficace, ce qui permet de gagner du temps lors de la programmation des ordinateurs pour diviser des nombres binaires. C'est la méthode de soustraction par compléments en binaire. Voici les bases, en calculant 111 - 011 (assurez-vous que les deux nombres ont la même longueur):
2 Apprenez à soustraire par des compléments. Bien que vous puissiez facilement utiliser la méthode ci-dessus en binaire, nous pouvons également soustraire par une méthode plus efficace, ce qui permet de gagner du temps lors de la programmation des ordinateurs pour diviser des nombres binaires. C'est la méthode de soustraction par compléments en binaire. Voici les bases, en calculant 111 - 011 (assurez-vous que les deux nombres ont la même longueur):  3 Combinez les deux concepts ci-dessus. Vous connaissez maintenant la méthode de soustraction des problèmes de division et la méthode du complément à deux pour résoudre les problèmes de soustraction. Vous pouvez combiner ceci en une seule méthode pour résoudre les problèmes de division, en utilisant les étapes ci-dessous.[9] Si vous le souhaitez, vous pouvez essayer de le comprendre vous-même avant de continuer.
3 Combinez les deux concepts ci-dessus. Vous connaissez maintenant la méthode de soustraction des problèmes de division et la méthode du complément à deux pour résoudre les problèmes de soustraction. Vous pouvez combiner ceci en une seule méthode pour résoudre les problèmes de division, en utilisant les étapes ci-dessous.[9] Si vous le souhaitez, vous pouvez essayer de le comprendre vous-même avant de continuer. 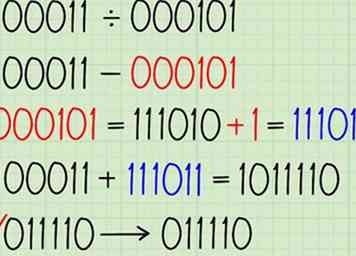 4 Soustrayez le diviseur du dividende en ajoutant deux compléments. Passons en revue le problème 100011 ÷ 000101. La première étape consiste à résoudre le problème 100011 - 000101, en utilisant la méthode du complément twos pour en faire un problème supplémentaire:
4 Soustrayez le diviseur du dividende en ajoutant deux compléments. Passons en revue le problème 100011 ÷ 000101. La première étape consiste à résoudre le problème 100011 - 000101, en utilisant la méthode du complément twos pour en faire un problème supplémentaire:  5 Ajoutez-en un au quotient. Dans un programme informatique, c'est le point où vous incrémentez le quotient de un. Sur papier, faites une note quelque part dans un coin où elle ne sera pas confondue avec votre autre travail. Nous avons soustrait une fois avec succès, donc le quotient jusqu'à présent est 1.
5 Ajoutez-en un au quotient. Dans un programme informatique, c'est le point où vous incrémentez le quotient de un. Sur papier, faites une note quelque part dans un coin où elle ne sera pas confondue avec votre autre travail. Nous avons soustrait une fois avec succès, donc le quotient jusqu'à présent est 1. 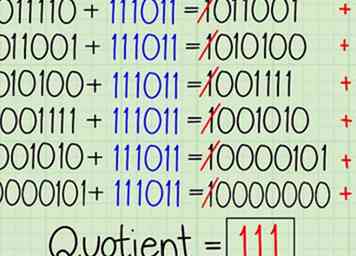 6 Répétez en soustrayant le diviseur du reste. Le résultat de notre dernier calcul est le reste qui reste après que le diviseur "est entré" une fois. Continuez à ajouter le complément à deux du diviseur à chaque fois et supprimez le bit de retenue. Ajoutez-en un au quotient à chaque fois, en répétant jusqu'à ce que vous obteniez un reste égal ou inférieur à votre diviseur:[10]
6 Répétez en soustrayant le diviseur du reste. Le résultat de notre dernier calcul est le reste qui reste après que le diviseur "est entré" une fois. Continuez à ajouter le complément à deux du diviseur à chaque fois et supprimez le bit de retenue. Ajoutez-en un au quotient à chaque fois, en répétant jusqu'à ce que vous obteniez un reste égal ou inférieur à votre diviseur:[10]