Un numéro facteurs sont des nombres qui se multiplient pour en faire un produit. Une autre façon de penser est que chaque nombre est le produit de plusieurs facteurs. Apprendre à prendre en compte, c'est-à-dire diviser un nombre en facteurs, est une compétence mathématique importante qui est utilisée non seulement en arithmétique de base, mais aussi en algèbre, en calcul et au-delà. Voir l'étape 1 ci-dessous pour commencer à apprendre à prendre en compte!
Méthode One of Two:
Factorisation des entiers de base
-
 1 Écrivez votre numéro Pour commencer la factorisation, tout ce dont vous avez besoin est un nombre - n'importe quel nombre le fera, mais pour notre propos, commençons par un entier simple. Entiers sont des nombres sans composants fractionnaires ou décimaux (tous les nombres entiers positifs et négatifs sont des nombres entiers).
1 Écrivez votre numéro Pour commencer la factorisation, tout ce dont vous avez besoin est un nombre - n'importe quel nombre le fera, mais pour notre propos, commençons par un entier simple. Entiers sont des nombres sans composants fractionnaires ou décimaux (tous les nombres entiers positifs et négatifs sont des nombres entiers). - Choisissons le nombre 12. Ecrivez ce numéro sur un morceau de papier brouillon.
-
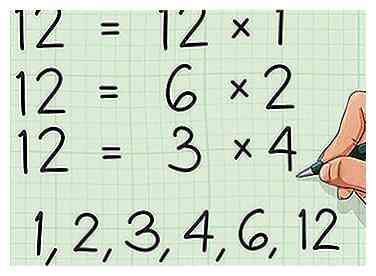 2 Trouvez deux autres nombres qui se multiplient pour faire votre premier numéro. Tout entier peut être écrit comme le produit de deux autres entiers. Même les nombres premiers peuvent être écrits comme le produit de 1 et le nombre lui-même. Penser à un nombre comme le produit de deux facteurs peut exiger une réflexion «en arrière» - vous devez essentiellement vous demander: «quel problème de multiplication équivaut à ce nombre?
2 Trouvez deux autres nombres qui se multiplient pour faire votre premier numéro. Tout entier peut être écrit comme le produit de deux autres entiers. Même les nombres premiers peuvent être écrits comme le produit de 1 et le nombre lui-même. Penser à un nombre comme le produit de deux facteurs peut exiger une réflexion «en arrière» - vous devez essentiellement vous demander: «quel problème de multiplication équivaut à ce nombre? - Dans notre exemple, 12 facteurs multiples - 12 × 1, 6 × 2 et 3 × 4 sont tous égaux à 12. Nous pouvons donc dire que les facteurs de 12 sont 1, 2, 3, 4, 6 et 12. Pour notre propos, travaillons avec les facteurs 6 et 2.
- Les nombres pairs sont particulièrement faciles à prendre en compte car chaque nombre pair a deux facteurs. 4 = 2 × 2, 26 = 13 × 2, etc.
-
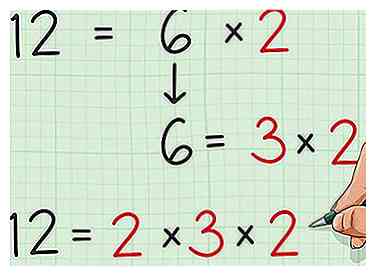 3 Déterminez si l'un de vos facteurs peut être à nouveau pris en compte. Beaucoup de nombres - en particulier les grands - peuvent être multipliés à plusieurs reprises. Lorsque vous avez trouvé deux facteurs, si vous avez un ensemble de facteurs, vous pouvez réduire ce nombre à ses facteurs aussi bien. Selon la situation, cela peut être bénéfique ou non.
3 Déterminez si l'un de vos facteurs peut être à nouveau pris en compte. Beaucoup de nombres - en particulier les grands - peuvent être multipliés à plusieurs reprises. Lorsque vous avez trouvé deux facteurs, si vous avez un ensemble de facteurs, vous pouvez réduire ce nombre à ses facteurs aussi bien. Selon la situation, cela peut être bénéfique ou non. - Par exemple, dans notre exemple, nous avons réduit 12 à 2 × 6. Notez que 6 a ses propres facteurs - 3 × 2 = 6. On peut donc dire que 12 = 2 × (3 × 2).
-
 4 Arrêtez la factorisation lorsque vous atteignez les nombres premiers. Les nombres premiers sont des nombres supérieurs à 1 qui ne sont divisibles que par eux-mêmes et 1. Par exemple, 2, 3, 5, 7, 11, 13 et 17 sont tous des nombres premiers. Lorsque vous avez pris en compte un nombre pour qu'il soit le produit de nombres premiers exclusivement, un affacturage supplémentaire est superflu. Il est inutile de réduire chaque facteur à lui-même fois, vous pouvez donc vous arrêter.
4 Arrêtez la factorisation lorsque vous atteignez les nombres premiers. Les nombres premiers sont des nombres supérieurs à 1 qui ne sont divisibles que par eux-mêmes et 1. Par exemple, 2, 3, 5, 7, 11, 13 et 17 sont tous des nombres premiers. Lorsque vous avez pris en compte un nombre pour qu'il soit le produit de nombres premiers exclusivement, un affacturage supplémentaire est superflu. Il est inutile de réduire chaque facteur à lui-même fois, vous pouvez donc vous arrêter. - Dans notre exemple, nous avons réduit 12 à 2 × (2 × 3). 2, 2 et 3 sont tous des nombres premiers. Si nous devions prendre davantage en compte, nous devions prendre en compte (2 × 1) × ((2 × 1) (3 × 1)), ce qui n'est généralement pas utile, et donc généralement évité.
-
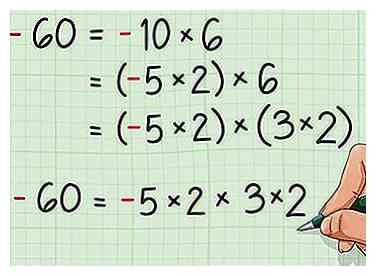 5 Facteur des nombres négatifs de la même manière. Les nombres négatifs peuvent être considérés de manière presque identique à la manière dont les nombres positifs sont pris en compte. La seule différence est que les facteurs doivent se multiplier pour donner un nombre négatif à leur produit, de sorte qu'un nombre impair de facteurs doit être négatif.
5 Facteur des nombres négatifs de la même manière. Les nombres négatifs peuvent être considérés de manière presque identique à la manière dont les nombres positifs sont pris en compte. La seule différence est que les facteurs doivent se multiplier pour donner un nombre négatif à leur produit, de sorte qu'un nombre impair de facteurs doit être négatif. - Par exemple, prenons le facteur -60. Voir ci-dessous:
- -60 = -10 × 6
- -60 = (-5 × 2) × 6
- -60 = (-5 × 2) × (3 × 2)
- -60 = -5 × 2 × 3 × 2. Notez que le fait d’avoir un nombre impair de nombres négatifs en plus de celui donne le même produit. Par exemple, -5 × 2 × -3 × -2 est également égal à 60.
- Par exemple, prenons le facteur -60. Voir ci-dessous:
Méthode deux sur deux:
Stratégie de factorisation des grands nombres
-
 1 Écrivez votre numéro au-dessus d'un tableau à deux colonnes. Bien qu'il soit généralement assez facile de prendre en compte de petits nombres entiers, des nombres plus importants peuvent être décourageants. La plupart d'entre nous auraient du mal à diviser un nombre à 4 ou 5 chiffres en facteurs premiers en n'utilisant que des calculs mentaux. Heureusement, en utilisant une table, le processus devient beaucoup plus facile. Écrivez votre numéro au-dessus d'une table en forme de T avec deux colonnes - vous utiliserez ce tableau pour suivre votre liste croissante de facteurs.
1 Écrivez votre numéro au-dessus d'un tableau à deux colonnes. Bien qu'il soit généralement assez facile de prendre en compte de petits nombres entiers, des nombres plus importants peuvent être décourageants. La plupart d'entre nous auraient du mal à diviser un nombre à 4 ou 5 chiffres en facteurs premiers en n'utilisant que des calculs mentaux. Heureusement, en utilisant une table, le processus devient beaucoup plus facile. Écrivez votre numéro au-dessus d'une table en forme de T avec deux colonnes - vous utiliserez ce tableau pour suivre votre liste croissante de facteurs. - Pour les besoins de notre exemple, choisissons un nombre à 4 chiffres pour prendre en compte - 6,552.
-
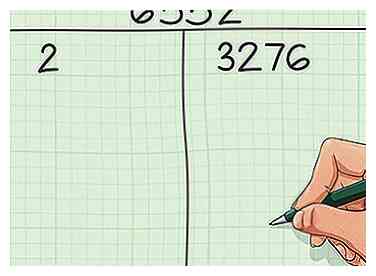 2 Divisez votre nombre par le plus petit facteur premier possible. Divisez votre nombre par le plus petit facteur premier (en plus de 1) qui se divise uniformément, sans reste. Écrivez le facteur premier dans la colonne de gauche et écrivez votre réponse en face dans la colonne de droite. Comme indiqué ci-dessus, les nombres pairs sont particulièrement faciles à commencer à prendre en compte car leur facteur premier le plus petit sera toujours 2. Les nombres impairs, par contre, auront les facteurs premiers les plus petits.
2 Divisez votre nombre par le plus petit facteur premier possible. Divisez votre nombre par le plus petit facteur premier (en plus de 1) qui se divise uniformément, sans reste. Écrivez le facteur premier dans la colonne de gauche et écrivez votre réponse en face dans la colonne de droite. Comme indiqué ci-dessus, les nombres pairs sont particulièrement faciles à commencer à prendre en compte car leur facteur premier le plus petit sera toujours 2. Les nombres impairs, par contre, auront les facteurs premiers les plus petits. - Dans notre exemple, puisque 6 552 est pair, nous savons que 2 est son plus petit facteur premier. 6,552 ÷ 2 = 3,276. Dans la colonne de gauche, nous écrirons 2, et dans la colonne de droite, écris 3,276.
-
 3 Continuer à prendre en compte de cette façon. Ensuite, factorisez le nombre dans la colonne de droite par son plus petit facteur premier, plutôt que le nombre en haut de la table. Écrivez le facteur premier dans la colonne de gauche et le nouveau nombre dans la colonne de droite. Continuez à répéter ce processus - à chaque répétition, le nombre dans la colonne de droite devrait diminuer.
3 Continuer à prendre en compte de cette façon. Ensuite, factorisez le nombre dans la colonne de droite par son plus petit facteur premier, plutôt que le nombre en haut de la table. Écrivez le facteur premier dans la colonne de gauche et le nouveau nombre dans la colonne de droite. Continuez à répéter ce processus - à chaque répétition, le nombre dans la colonne de droite devrait diminuer. - Continuons notre processus. 3 276 ÷ 2 = 1 638, donc au bas de la colonne de gauche, nous écrirons un autre 2, et au bas de la colonne de droite, nous écrirons 1,638. 1,638 ÷ 2 = 819, nous écrirons donc 2 et 819 au bas des deux colonnes comme avant.
-
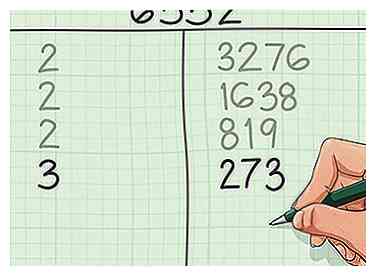 4 Traiter les nombres impairs en essayant de petits facteurs premiers. Les nombres impairs sont plus difficiles à trouver le plus petit facteur premier que les nombres pairs, car ils n’ont pas automatiquement le facteur premier le plus petit. Lorsque vous atteignez un nombre impair, essayez de diviser par de petits nombres premiers autres que 2 - 3, 5, 7, 11, etc. C'est le plus petit facteur premier du numéro.
4 Traiter les nombres impairs en essayant de petits facteurs premiers. Les nombres impairs sont plus difficiles à trouver le plus petit facteur premier que les nombres pairs, car ils n’ont pas automatiquement le facteur premier le plus petit. Lorsque vous atteignez un nombre impair, essayez de diviser par de petits nombres premiers autres que 2 - 3, 5, 7, 11, etc. C'est le plus petit facteur premier du numéro. - Dans notre exemple, nous avons atteint 819. 819 est étrange, donc 2 n'est pas un facteur de 819.Au lieu d'écrire un autre 2, nous essaierons le nombre premier suivant: 3. 819 = 3 = 273 sans reste, nous allons donc écrire 3 et 273.
- Lorsque vous devinez des facteurs, vous devriez essayer tous les nombres premiers jusqu'à la racine carrée du facteur le plus important trouvé jusqu'ici. Si aucun des facteurs que vous essayez jusqu'à présent ne divise de manière égale, vous essayez probablement de prendre en compte un nombre premier et vous finissez donc avec le processus de factorisation.
-
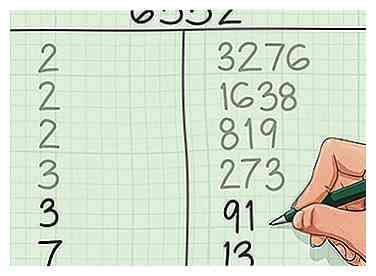 5 Continuez jusqu'à ce que vous atteigniez 1. Continuez à diviser les nombres dans la colonne de droite par leur plus petit facteur premier jusqu'à ce que vous obteniez un nombre premier dans la colonne de droite. Diviser ce nombre par lui-même - cela mettra le nombre dans la colonne de gauche et "1" dans la colonne de droite.
5 Continuez jusqu'à ce que vous atteigniez 1. Continuez à diviser les nombres dans la colonne de droite par leur plus petit facteur premier jusqu'à ce que vous obteniez un nombre premier dans la colonne de droite. Diviser ce nombre par lui-même - cela mettra le nombre dans la colonne de gauche et "1" dans la colonne de droite. - Finissons d'affecter notre numéro. Voir ci-dessous pour une ventilation détaillée:
- Diviser par 3 encore: 273 ÷ 3 = 91, pas de reste, donc nous allons écrire 3 et 91.
- Essayons à nouveau 3: 91 n'a pas de facteur 3, ni le facteur premier le plus bas (5) comme facteur, mais 91 ÷ 7 = 13, sans reste, donc nous noterons 7 et 13.
- Essayons à nouveau 7: 13 n'a pas 7 comme facteur, ou 11 (le prochain nombre premier), mais il a lui-même un facteur: 13 ÷ 13 = 1. Donc, pour terminer notre table, nous allons écrire 13 et 1. Nous pouvons enfin arrêter l'affacturage.
- Finissons d'affecter notre numéro. Voir ci-dessous pour une ventilation détaillée:
-
 6 Utilisez les chiffres dans la colonne de gauche comme facteurs de votre numéro d'origine. Une fois que vous avez atteint 1 dans la colonne de droite, vous avez terminé. Les nombres figurant sur le côté gauche du tableau sont vos facteurs. En d'autres termes, le produit lorsque vous multipliez tous ces nombres ensemble sera le nombre en haut du tableau. Si le même facteur apparaît plusieurs fois, vous pouvez utiliser la notation des exposants pour économiser de l'espace. Par exemple, si votre liste de facteurs a quatre 2, vous pouvez écrire 24 plutôt que 2 × 2 × 2 × 2.
6 Utilisez les chiffres dans la colonne de gauche comme facteurs de votre numéro d'origine. Une fois que vous avez atteint 1 dans la colonne de droite, vous avez terminé. Les nombres figurant sur le côté gauche du tableau sont vos facteurs. En d'autres termes, le produit lorsque vous multipliez tous ces nombres ensemble sera le nombre en haut du tableau. Si le même facteur apparaît plusieurs fois, vous pouvez utiliser la notation des exposants pour économiser de l'espace. Par exemple, si votre liste de facteurs a quatre 2, vous pouvez écrire 24 plutôt que 2 × 2 × 2 × 2. - Dans notre exemple 6 552 = 23 × 32 × 7 × 13. C'est la factorisation complète de 6 552 en nombres premiers. Quel que soit l'ordre dans lequel ces chiffres sont multipliés, le produit sera 6 552.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Écrivez votre numéro Pour commencer la factorisation, tout ce dont vous avez besoin est un nombre - n'importe quel nombre le fera, mais pour notre propos, commençons par un entier simple. Entiers sont des nombres sans composants fractionnaires ou décimaux (tous les nombres entiers positifs et négatifs sont des nombres entiers).
1 Écrivez votre numéro Pour commencer la factorisation, tout ce dont vous avez besoin est un nombre - n'importe quel nombre le fera, mais pour notre propos, commençons par un entier simple. Entiers sont des nombres sans composants fractionnaires ou décimaux (tous les nombres entiers positifs et négatifs sont des nombres entiers). 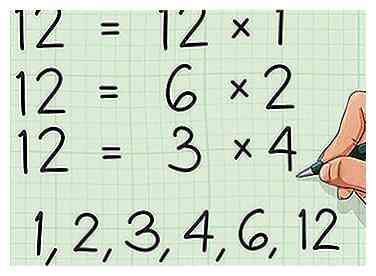 2 Trouvez deux autres nombres qui se multiplient pour faire votre premier numéro. Tout entier peut être écrit comme le produit de deux autres entiers. Même les nombres premiers peuvent être écrits comme le produit de 1 et le nombre lui-même. Penser à un nombre comme le produit de deux facteurs peut exiger une réflexion «en arrière» - vous devez essentiellement vous demander: «quel problème de multiplication équivaut à ce nombre?
2 Trouvez deux autres nombres qui se multiplient pour faire votre premier numéro. Tout entier peut être écrit comme le produit de deux autres entiers. Même les nombres premiers peuvent être écrits comme le produit de 1 et le nombre lui-même. Penser à un nombre comme le produit de deux facteurs peut exiger une réflexion «en arrière» - vous devez essentiellement vous demander: «quel problème de multiplication équivaut à ce nombre? 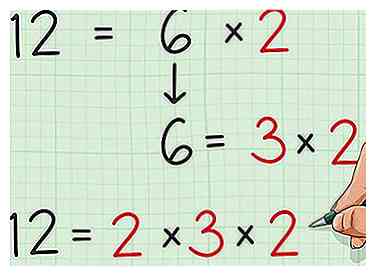 3 Déterminez si l'un de vos facteurs peut être à nouveau pris en compte. Beaucoup de nombres - en particulier les grands - peuvent être multipliés à plusieurs reprises. Lorsque vous avez trouvé deux facteurs, si vous avez un ensemble de facteurs, vous pouvez réduire ce nombre à ses facteurs aussi bien. Selon la situation, cela peut être bénéfique ou non.
3 Déterminez si l'un de vos facteurs peut être à nouveau pris en compte. Beaucoup de nombres - en particulier les grands - peuvent être multipliés à plusieurs reprises. Lorsque vous avez trouvé deux facteurs, si vous avez un ensemble de facteurs, vous pouvez réduire ce nombre à ses facteurs aussi bien. Selon la situation, cela peut être bénéfique ou non.  4 Arrêtez la factorisation lorsque vous atteignez les nombres premiers. Les nombres premiers sont des nombres supérieurs à 1 qui ne sont divisibles que par eux-mêmes et 1. Par exemple, 2, 3, 5, 7, 11, 13 et 17 sont tous des nombres premiers. Lorsque vous avez pris en compte un nombre pour qu'il soit le produit de nombres premiers exclusivement, un affacturage supplémentaire est superflu. Il est inutile de réduire chaque facteur à lui-même fois, vous pouvez donc vous arrêter.
4 Arrêtez la factorisation lorsque vous atteignez les nombres premiers. Les nombres premiers sont des nombres supérieurs à 1 qui ne sont divisibles que par eux-mêmes et 1. Par exemple, 2, 3, 5, 7, 11, 13 et 17 sont tous des nombres premiers. Lorsque vous avez pris en compte un nombre pour qu'il soit le produit de nombres premiers exclusivement, un affacturage supplémentaire est superflu. Il est inutile de réduire chaque facteur à lui-même fois, vous pouvez donc vous arrêter. 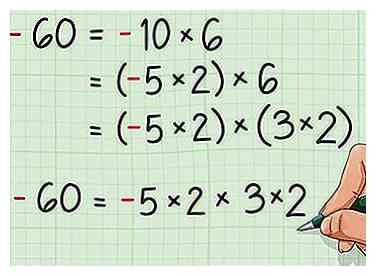 5 Facteur des nombres négatifs de la même manière. Les nombres négatifs peuvent être considérés de manière presque identique à la manière dont les nombres positifs sont pris en compte. La seule différence est que les facteurs doivent se multiplier pour donner un nombre négatif à leur produit, de sorte qu'un nombre impair de facteurs doit être négatif.
5 Facteur des nombres négatifs de la même manière. Les nombres négatifs peuvent être considérés de manière presque identique à la manière dont les nombres positifs sont pris en compte. La seule différence est que les facteurs doivent se multiplier pour donner un nombre négatif à leur produit, de sorte qu'un nombre impair de facteurs doit être négatif.  1 Écrivez votre numéro au-dessus d'un tableau à deux colonnes. Bien qu'il soit généralement assez facile de prendre en compte de petits nombres entiers, des nombres plus importants peuvent être décourageants. La plupart d'entre nous auraient du mal à diviser un nombre à 4 ou 5 chiffres en facteurs premiers en n'utilisant que des calculs mentaux. Heureusement, en utilisant une table, le processus devient beaucoup plus facile. Écrivez votre numéro au-dessus d'une table en forme de T avec deux colonnes - vous utiliserez ce tableau pour suivre votre liste croissante de facteurs.
1 Écrivez votre numéro au-dessus d'un tableau à deux colonnes. Bien qu'il soit généralement assez facile de prendre en compte de petits nombres entiers, des nombres plus importants peuvent être décourageants. La plupart d'entre nous auraient du mal à diviser un nombre à 4 ou 5 chiffres en facteurs premiers en n'utilisant que des calculs mentaux. Heureusement, en utilisant une table, le processus devient beaucoup plus facile. Écrivez votre numéro au-dessus d'une table en forme de T avec deux colonnes - vous utiliserez ce tableau pour suivre votre liste croissante de facteurs.  2 Divisez votre nombre par le plus petit facteur premier possible. Divisez votre nombre par le plus petit facteur premier (en plus de 1) qui se divise uniformément, sans reste. Écrivez le facteur premier dans la colonne de gauche et écrivez votre réponse en face dans la colonne de droite. Comme indiqué ci-dessus, les nombres pairs sont particulièrement faciles à commencer à prendre en compte car leur facteur premier le plus petit sera toujours 2. Les nombres impairs, par contre, auront les facteurs premiers les plus petits.
2 Divisez votre nombre par le plus petit facteur premier possible. Divisez votre nombre par le plus petit facteur premier (en plus de 1) qui se divise uniformément, sans reste. Écrivez le facteur premier dans la colonne de gauche et écrivez votre réponse en face dans la colonne de droite. Comme indiqué ci-dessus, les nombres pairs sont particulièrement faciles à commencer à prendre en compte car leur facteur premier le plus petit sera toujours 2. Les nombres impairs, par contre, auront les facteurs premiers les plus petits.  3 Continuer à prendre en compte de cette façon. Ensuite, factorisez le nombre dans la colonne de droite par son plus petit facteur premier, plutôt que le nombre en haut de la table. Écrivez le facteur premier dans la colonne de gauche et le nouveau nombre dans la colonne de droite. Continuez à répéter ce processus - à chaque répétition, le nombre dans la colonne de droite devrait diminuer.
3 Continuer à prendre en compte de cette façon. Ensuite, factorisez le nombre dans la colonne de droite par son plus petit facteur premier, plutôt que le nombre en haut de la table. Écrivez le facteur premier dans la colonne de gauche et le nouveau nombre dans la colonne de droite. Continuez à répéter ce processus - à chaque répétition, le nombre dans la colonne de droite devrait diminuer.  4 Traiter les nombres impairs en essayant de petits facteurs premiers. Les nombres impairs sont plus difficiles à trouver le plus petit facteur premier que les nombres pairs, car ils n’ont pas automatiquement le facteur premier le plus petit. Lorsque vous atteignez un nombre impair, essayez de diviser par de petits nombres premiers autres que 2 - 3, 5, 7, 11, etc. C'est le plus petit facteur premier du numéro.
4 Traiter les nombres impairs en essayant de petits facteurs premiers. Les nombres impairs sont plus difficiles à trouver le plus petit facteur premier que les nombres pairs, car ils n’ont pas automatiquement le facteur premier le plus petit. Lorsque vous atteignez un nombre impair, essayez de diviser par de petits nombres premiers autres que 2 - 3, 5, 7, 11, etc. C'est le plus petit facteur premier du numéro.  5 Continuez jusqu'à ce que vous atteigniez 1. Continuez à diviser les nombres dans la colonne de droite par leur plus petit facteur premier jusqu'à ce que vous obteniez un nombre premier dans la colonne de droite. Diviser ce nombre par lui-même - cela mettra le nombre dans la colonne de gauche et "1" dans la colonne de droite.
5 Continuez jusqu'à ce que vous atteigniez 1. Continuez à diviser les nombres dans la colonne de droite par leur plus petit facteur premier jusqu'à ce que vous obteniez un nombre premier dans la colonne de droite. Diviser ce nombre par lui-même - cela mettra le nombre dans la colonne de gauche et "1" dans la colonne de droite.  6 Utilisez les chiffres dans la colonne de gauche comme facteurs de votre numéro d'origine. Une fois que vous avez atteint 1 dans la colonne de droite, vous avez terminé. Les nombres figurant sur le côté gauche du tableau sont vos facteurs. En d'autres termes, le produit lorsque vous multipliez tous ces nombres ensemble sera le nombre en haut du tableau. Si le même facteur apparaît plusieurs fois, vous pouvez utiliser la notation des exposants pour économiser de l'espace. Par exemple, si votre liste de facteurs a quatre 2, vous pouvez écrire 24 plutôt que 2 × 2 × 2 × 2.
6 Utilisez les chiffres dans la colonne de gauche comme facteurs de votre numéro d'origine. Une fois que vous avez atteint 1 dans la colonne de droite, vous avez terminé. Les nombres figurant sur le côté gauche du tableau sont vos facteurs. En d'autres termes, le produit lorsque vous multipliez tous ces nombres ensemble sera le nombre en haut du tableau. Si le même facteur apparaît plusieurs fois, vous pouvez utiliser la notation des exposants pour économiser de l'espace. Par exemple, si votre liste de facteurs a quatre 2, vous pouvez écrire 24 plutôt que 2 × 2 × 2 × 2.