La factorisation prime divise un nombre en ses blocs de construction les plus simples. Si vous détestez travailler avec de grands nombres comme 5 733, apprenez à le transformer en 3 x 3 x 7 x 7 x 13 à la place. Ce type de problème est essentiel à la cryptographie ou aux techniques utilisées pour sécuriser les informations. Si vous n'êtes pas encore prêt à créer votre propre système de messagerie électronique, essayez d'utiliser la factorisation par facteurs pour faciliter les fractions.
Première partie de deux:
Trouver la première factorisation
-
 1 Comprendre la factorisation. La factorisation est le processus consistant à "décomposer" un nombre en parties plus petites. Ces parties, ou facteurs, se multiplient pour être égales au nombre d'origine.
1 Comprendre la factorisation. La factorisation est le processus consistant à "décomposer" un nombre en parties plus petites. Ces parties, ou facteurs, se multiplient pour être égales au nombre d'origine. - Par exemple, pour factoriser le nombre 18, divisez-le en 1 x 18 ou en 2 x 9 ou en 3 x 6.
-
 2 Revoir les nombres premiers. Un nombre premier n'a que deux facteurs: lui-même et 1. Le nombre 5, par exemple, est le produit de 5 et 1. Vous ne pouvez pas le décomposer en d'autres nombres. Le but de la factorisation en nombres premiers est de continuer à décomposer un nombre jusqu'à ce qu'il ne reste plus que des nombres premiers. Ceci est particulièrement utile lors de la manipulation de fractions, ce qui les rend plus faciles à comparer et à utiliser dans les équations.[1]
2 Revoir les nombres premiers. Un nombre premier n'a que deux facteurs: lui-même et 1. Le nombre 5, par exemple, est le produit de 5 et 1. Vous ne pouvez pas le décomposer en d'autres nombres. Le but de la factorisation en nombres premiers est de continuer à décomposer un nombre jusqu'à ce qu'il ne reste plus que des nombres premiers. Ceci est particulièrement utile lors de la manipulation de fractions, ce qui les rend plus faciles à comparer et à utiliser dans les équations.[1] -
 3 Commencez avec un numéro. Choisissez un nombre non premier supérieur à 3. Il n'y a aucun point commençant par un nombre premier, car il n'y a aucun moyen de le factoriser.
3 Commencez avec un numéro. Choisissez un nombre non premier supérieur à 3. Il n'y a aucun point commençant par un nombre premier, car il n'y a aucun moyen de le factoriser. - Exemple: Dans ce guide, nous trouvons la factorisation en nombres premiers de 24.
-
 4 Factez le en deux nombres. Trouvez deux nombres qui se multiplient pour créer le numéro avec lequel vous avez commencé. Vous pouvez en utiliser deux, mais un nombre premier facilitera votre travail. Une bonne stratégie consiste à diviser le nombre par 2, puis 3, puis 5, en remontant les nombres premiers jusqu'à ce que vous en trouviez un qui se divise également.
4 Factez le en deux nombres. Trouvez deux nombres qui se multiplient pour créer le numéro avec lequel vous avez commencé. Vous pouvez en utiliser deux, mais un nombre premier facilitera votre travail. Une bonne stratégie consiste à diviser le nombre par 2, puis 3, puis 5, en remontant les nombres premiers jusqu'à ce que vous en trouviez un qui se divise également. - Exemple: Si vous ne connaissez aucun facteur de 24, essayez de le diviser en petits nombres premiers. Divisons par 2 pour obtenir 24 = 2 x 12. Nous n'avons pas encore fini, mais c'est un bon début.
- Puisque 2 est primordial, c'est un moyen facile de commencer en tenant compte de tout nombre pair.
-
 5 Commencez à créer un arbre de facteurs. Un arbre de facteurs est un moyen facile de suivre un problème de factorisation.[2] Pour en démarrer une, il suffit de dessiner deux "branches" séparées du nombre d'origine. Écrivez vos deux facteurs à la fin de ces branches.
5 Commencez à créer un arbre de facteurs. Un arbre de facteurs est un moyen facile de suivre un problème de factorisation.[2] Pour en démarrer une, il suffit de dessiner deux "branches" séparées du nombre d'origine. Écrivez vos deux facteurs à la fin de ces branches. - Exemple:
- 24
- /\
- 2 12
-
 6 Factorisez la prochaine ligne de chiffres. Regardez vos deux nouveaux numéros (la deuxième ligne de votre arbre de facteurs). Sont-ils les deux premiers? Si l'un d'eux n'est pas un facteur primordial, reprenez-le de la même manière. Dessinez plus de branches sur l'arbre et écrivez les nouveaux facteurs sur une troisième ligne.
6 Factorisez la prochaine ligne de chiffres. Regardez vos deux nouveaux numéros (la deuxième ligne de votre arbre de facteurs). Sont-ils les deux premiers? Si l'un d'eux n'est pas un facteur primordial, reprenez-le de la même manière. Dessinez plus de branches sur l'arbre et écrivez les nouveaux facteurs sur une troisième ligne. - Exemple: 12 n'est pas un prime, donc nous le reprenons. Utilisons 12 = 2 x 6 et ajoutons-le à l'arbre de facteurs:
- 24
- /\
- 2 12
- /\
- 2 x 6
-
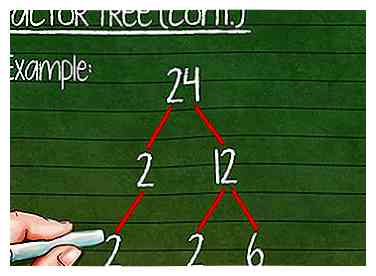 7 Faites tomber le prime. Si l'un des facteurs est primordial, ramenez-le à la ligne suivante avec sa propre "branche". Il n'y a pas moyen de le décomposer davantage, alors nous ne faisons que suivre pour l'instant.
7 Faites tomber le prime. Si l'un des facteurs est primordial, ramenez-le à la ligne suivante avec sa propre "branche". Il n'y a pas moyen de le décomposer davantage, alors nous ne faisons que suivre pour l'instant. - Exemple: 2 est un nombre premier. Apportez le 2 de la deuxième ligne au troisième.
- 24
- /\
- 2 12
- / /\
- 2 2 6
-
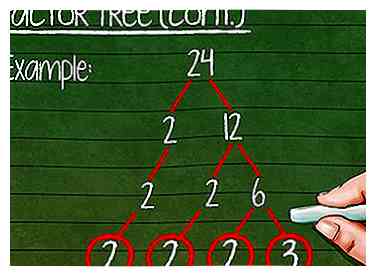 8 Continuez à factoriser jusqu'à ce qu'il ne vous reste plus que des nombres premiers. Vérifiez chaque nouvelle ligne de l'arborescence de facteurs une fois que vous l'avez écrite. Si l'un des nombres peut être à nouveau pris en compte, créez une nouvelle ligne. Vous avez terminé une fois qu'il ne reste plus que des nombres premiers.
8 Continuez à factoriser jusqu'à ce qu'il ne vous reste plus que des nombres premiers. Vérifiez chaque nouvelle ligne de l'arborescence de facteurs une fois que vous l'avez écrite. Si l'un des nombres peut être à nouveau pris en compte, créez une nouvelle ligne. Vous avez terminé une fois qu'il ne reste plus que des nombres premiers. - Exemple: 6 est un nombre non premier et doit être à nouveau pris en compte. 2 est un nombre premier, nous ramène donc les 2 à la ligne suivante.
- 24
- /\
- 2 12
- / /\
- 2 2 6
- / / /\
- 2 2 2 3
-
 9 Écrivez la dernière ligne comme facteurs premiers. Finalement, vous n'aurez plus que des nombres premiers. Lorsque cela se produit, vous avez terminé la factorisation. La factorisation principale est la dernière ligne entière des nombres, écrite comme un problème de multiplication.
9 Écrivez la dernière ligne comme facteurs premiers. Finalement, vous n'aurez plus que des nombres premiers. Lorsque cela se produit, vous avez terminé la factorisation. La factorisation principale est la dernière ligne entière des nombres, écrite comme un problème de multiplication. - Vérifiez votre travail en multipliant la dernière ligne. Il devrait être égal au numéro d'origine.
- Exemple: La dernière ligne de notre arbre de facteurs n'a que 2 et 3. Ce sont les deux nombres premiers, donc nous avons terminé. Nous pouvons écrire la factorisation première de 24 comme 24 = 2 x 2 x 2 x 3.
- L'ordre des facteurs n'a pas d'importance. 2 x 3 x 2 x 2 est également une bonne réponse.
-
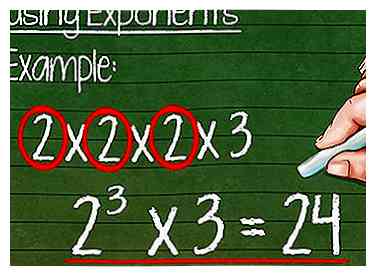 10 Simplifier l'utilisation des exposants (facultatif). Si vous savez écrire des exposants, vous pouvez rendre la factorisation plus facile à lire. Rappelez-vous qu'un exposant est un nombre de base suivi d'un élevé nombre qui indique combien de fois la base est multipliée.
10 Simplifier l'utilisation des exposants (facultatif). Si vous savez écrire des exposants, vous pouvez rendre la factorisation plus facile à lire. Rappelez-vous qu'un exposant est un nombre de base suivi d'un élevé nombre qui indique combien de fois la base est multipliée. - Exemple: Dans la factorisation 2 x 2 x 2 x 3, combien de fois 2 apparaît-il? Puisque la réponse est "trois", nous pouvons simplifier 2 x 2 x 2 avec 23. La factorisation simplifiée est 23 x 3.
Deuxième partie de deux:
Utilisation de la factorisation par prime
-
 1 Trouvez le plus grand facteur commun de deux nombres. Le plus grand facteur commun (GCF) de deux nombres est le plus grand nombre représentant un facteur des deux nombres. Voici comment trouver le GCF de 30 et de 36, en utilisant la factorisation en facteurs premiers:
1 Trouvez le plus grand facteur commun de deux nombres. Le plus grand facteur commun (GCF) de deux nombres est le plus grand nombre représentant un facteur des deux nombres. Voici comment trouver le GCF de 30 et de 36, en utilisant la factorisation en facteurs premiers: - Trouvez les factorisations premières des deux nombres. La factorisation de 30 est 2 x 3 x 5. La factorisation de 36 est 2 x 2 x 3 x 3.
- Recherchez un nombre qui apparaît sur les deux premières factorisations. Croisez-le une fois sur chaque liste et écrivez-le sur une nouvelle ligne. Par exemple, 2 est sur les deux listes, donc nous écrivons 2 sur une nouvelle ligne. Nous sommes partis avec 30 =
2x 3 x 5 et 36 =2x 2 x 3 x 3. - Répétez jusqu'à ce qu'il n'y ait plus de facteurs en commun. Il y a aussi un 3 sur les deux listes, alors écrivez-le sur votre nouvelle ligne pour faire 2 et 3. Comparer 30 =
2 x 3x 5 et 36 =2x 2 x3x 3. Il n'y a plus de nombres en commun. - Pour trouver le GCF, multipliez tous les facteurs partagés. Nous avons juste 2 et 3 dans notre exemple, donc le GCF est 2 x 3 = 6. C'est le plus grand nombre à la fois un facteur de 30 et un facteur de 36.
-
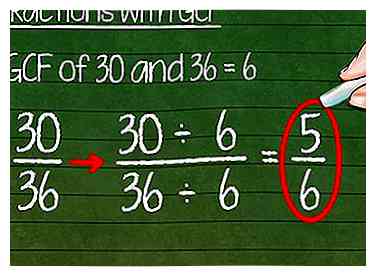 2 Simplifiez les fractions avec le GCF. Utilisez le facteur le plus commun chaque fois que vous pensez qu'une fraction n'est pas la plus simple. Trouvez le GCF du numérateur et du dénominateur, en utilisant le processus ci-dessus.Une fois que vous l'avez trouvé, divisez les deux parties de la fraction par le GCF.[3] La réponse sera la même fraction dans la forme la plus simple.
2 Simplifiez les fractions avec le GCF. Utilisez le facteur le plus commun chaque fois que vous pensez qu'une fraction n'est pas la plus simple. Trouvez le GCF du numérateur et du dénominateur, en utilisant le processus ci-dessus.Une fois que vous l'avez trouvé, divisez les deux parties de la fraction par le GCF.[3] La réponse sera la même fraction dans la forme la plus simple. - Par exemple, simplifiez la fraction 30/36. Nous avons déjà découvert que le GCF est 6, divisez donc le numérateur et le dénominateur par 6:
- 30 ÷ 6 = 5
- 36 ÷ 6 = 6
- 30/36 = 5/6
-
 3 Trouvez le plus petit multiple commun de deux nombres. Le plus petit multiple commun (LCM) de deux nombres est le plus petit nombre qui a les deux premiers nombres comme facteurs. Par exemple, le LCM de 2 et 3 est 6, car les deux facteurs sont 2 et 3. Voici un exemple de recherche de LCM à partir de la factorisation:
3 Trouvez le plus petit multiple commun de deux nombres. Le plus petit multiple commun (LCM) de deux nombres est le plus petit nombre qui a les deux premiers nombres comme facteurs. Par exemple, le LCM de 2 et 3 est 6, car les deux facteurs sont 2 et 3. Voici un exemple de recherche de LCM à partir de la factorisation: - Commencez avec deux factorisations premières. Par exemple, la factorisation en premier de 126 est 2 x 3 x 3 x 7. La factorisation initiale de 84 est 2 x 2 x 3 x 7.
- Pour chaque facteur unique, comparez le nombre de fois qu'il apparaît dans chaque liste. Choisissez une liste où il apparaît le plus grand nombre de fois et entourez chaque instance. Par exemple, 2 apparaît une fois dans les facteurs 126, mais deux fois dans la liste pour 84. Encerclez la 2 x 2 dans la deuxième liste.
- Répétez pour chaque facteur unique. Par exemple, 3 apparaît le plus souvent dans la première liste, alors encerclez la 3 x 3 Là. 7 apparaît seulement une fois sur chaque liste, encerclez donc un seul 7. (Peu importe la liste que vous choisissez quand il y a une cravate.)
- Multipliez tous vos nombres encerclés pour trouver le LCM. Dans notre exemple, le plus petit multiple commun de 126 et 84 est 2 x 2 x 3 x 3 x 7 = 252. C'est le plus petit nombre qui a à la fois 126 et 84 comme facteurs.
-
 4 Utilisez le LCM pour ajouter des fractions. Avant de pouvoir ajouter deux fractions ensemble, leurs dénominateurs doivent être les mêmes. Trouvez le plus petit commun multiple des deux dénominateurs. Multipliez chaque fraction de sorte que le nouveau dénominateur soit le LCM. Une fois que les deux fractions sont dans cette forme, vous pouvez les ajouter ensemble.
4 Utilisez le LCM pour ajouter des fractions. Avant de pouvoir ajouter deux fractions ensemble, leurs dénominateurs doivent être les mêmes. Trouvez le plus petit commun multiple des deux dénominateurs. Multipliez chaque fraction de sorte que le nouveau dénominateur soit le LCM. Une fois que les deux fractions sont dans cette forme, vous pouvez les ajouter ensemble. - Par exemple, nous voulons résoudre 1/6 + 4/21.
- En utilisant la méthode ci-dessus, nous pouvons trouver le LCM de 6 et 21. La réponse est 42.
- Tour 1/6 en une fraction avec 42 comme dénominateur. Pour ce faire, résolvez 42 ÷ 6 = 7. Multipliez 1/6 X 7/7 = 7/42.
- Tourner 4/21 en une fraction avec 42 comme dénominateur, résolvez 42 ÷ 21 = 2. Multipliez 4/21 X 2/2 = 8/42.
- Maintenant que nous avons les fractions sous des formes avec le même dénominateur, nous pouvons les ajouter facilement ensemble: 7/42 + 8/42 = 15/42.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Comprendre la factorisation. La factorisation est le processus consistant à "décomposer" un nombre en parties plus petites. Ces parties, ou facteurs, se multiplient pour être égales au nombre d'origine.
1 Comprendre la factorisation. La factorisation est le processus consistant à "décomposer" un nombre en parties plus petites. Ces parties, ou facteurs, se multiplient pour être égales au nombre d'origine.  2 Revoir les nombres premiers. Un nombre premier n'a que deux facteurs: lui-même et 1. Le nombre 5, par exemple, est le produit de 5 et 1. Vous ne pouvez pas le décomposer en d'autres nombres. Le but de la factorisation en nombres premiers est de continuer à décomposer un nombre jusqu'à ce qu'il ne reste plus que des nombres premiers. Ceci est particulièrement utile lors de la manipulation de fractions, ce qui les rend plus faciles à comparer et à utiliser dans les équations.[1]
2 Revoir les nombres premiers. Un nombre premier n'a que deux facteurs: lui-même et 1. Le nombre 5, par exemple, est le produit de 5 et 1. Vous ne pouvez pas le décomposer en d'autres nombres. Le but de la factorisation en nombres premiers est de continuer à décomposer un nombre jusqu'à ce qu'il ne reste plus que des nombres premiers. Ceci est particulièrement utile lors de la manipulation de fractions, ce qui les rend plus faciles à comparer et à utiliser dans les équations.[1]  3 Commencez avec un numéro. Choisissez un nombre non premier supérieur à 3. Il n'y a aucun point commençant par un nombre premier, car il n'y a aucun moyen de le factoriser.
3 Commencez avec un numéro. Choisissez un nombre non premier supérieur à 3. Il n'y a aucun point commençant par un nombre premier, car il n'y a aucun moyen de le factoriser.  4 Factez le en deux nombres. Trouvez deux nombres qui se multiplient pour créer le numéro avec lequel vous avez commencé. Vous pouvez en utiliser deux, mais un nombre premier facilitera votre travail. Une bonne stratégie consiste à diviser le nombre par 2, puis 3, puis 5, en remontant les nombres premiers jusqu'à ce que vous en trouviez un qui se divise également.
4 Factez le en deux nombres. Trouvez deux nombres qui se multiplient pour créer le numéro avec lequel vous avez commencé. Vous pouvez en utiliser deux, mais un nombre premier facilitera votre travail. Une bonne stratégie consiste à diviser le nombre par 2, puis 3, puis 5, en remontant les nombres premiers jusqu'à ce que vous en trouviez un qui se divise également.  5 Commencez à créer un arbre de facteurs. Un arbre de facteurs est un moyen facile de suivre un problème de factorisation.[2] Pour en démarrer une, il suffit de dessiner deux "branches" séparées du nombre d'origine. Écrivez vos deux facteurs à la fin de ces branches.
5 Commencez à créer un arbre de facteurs. Un arbre de facteurs est un moyen facile de suivre un problème de factorisation.[2] Pour en démarrer une, il suffit de dessiner deux "branches" séparées du nombre d'origine. Écrivez vos deux facteurs à la fin de ces branches.  6 Factorisez la prochaine ligne de chiffres. Regardez vos deux nouveaux numéros (la deuxième ligne de votre arbre de facteurs). Sont-ils les deux premiers? Si l'un d'eux n'est pas un facteur primordial, reprenez-le de la même manière. Dessinez plus de branches sur l'arbre et écrivez les nouveaux facteurs sur une troisième ligne.
6 Factorisez la prochaine ligne de chiffres. Regardez vos deux nouveaux numéros (la deuxième ligne de votre arbre de facteurs). Sont-ils les deux premiers? Si l'un d'eux n'est pas un facteur primordial, reprenez-le de la même manière. Dessinez plus de branches sur l'arbre et écrivez les nouveaux facteurs sur une troisième ligne.  7 Faites tomber le prime. Si l'un des facteurs est primordial, ramenez-le à la ligne suivante avec sa propre "branche". Il n'y a pas moyen de le décomposer davantage, alors nous ne faisons que suivre pour l'instant.
7 Faites tomber le prime. Si l'un des facteurs est primordial, ramenez-le à la ligne suivante avec sa propre "branche". Il n'y a pas moyen de le décomposer davantage, alors nous ne faisons que suivre pour l'instant.  8 Continuez à factoriser jusqu'à ce qu'il ne vous reste plus que des nombres premiers. Vérifiez chaque nouvelle ligne de l'arborescence de facteurs une fois que vous l'avez écrite. Si l'un des nombres peut être à nouveau pris en compte, créez une nouvelle ligne. Vous avez terminé une fois qu'il ne reste plus que des nombres premiers.
8 Continuez à factoriser jusqu'à ce qu'il ne vous reste plus que des nombres premiers. Vérifiez chaque nouvelle ligne de l'arborescence de facteurs une fois que vous l'avez écrite. Si l'un des nombres peut être à nouveau pris en compte, créez une nouvelle ligne. Vous avez terminé une fois qu'il ne reste plus que des nombres premiers.  9 Écrivez la dernière ligne comme facteurs premiers. Finalement, vous n'aurez plus que des nombres premiers. Lorsque cela se produit, vous avez terminé la factorisation. La factorisation principale est la dernière ligne entière des nombres, écrite comme un problème de multiplication.
9 Écrivez la dernière ligne comme facteurs premiers. Finalement, vous n'aurez plus que des nombres premiers. Lorsque cela se produit, vous avez terminé la factorisation. La factorisation principale est la dernière ligne entière des nombres, écrite comme un problème de multiplication. 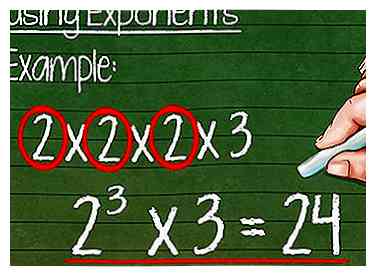 10 Simplifier l'utilisation des exposants (facultatif). Si vous savez écrire des exposants, vous pouvez rendre la factorisation plus facile à lire. Rappelez-vous qu'un exposant est un nombre de base suivi d'un élevé nombre qui indique combien de fois la base est multipliée.
10 Simplifier l'utilisation des exposants (facultatif). Si vous savez écrire des exposants, vous pouvez rendre la factorisation plus facile à lire. Rappelez-vous qu'un exposant est un nombre de base suivi d'un élevé nombre qui indique combien de fois la base est multipliée.  1 Trouvez le plus grand facteur commun de deux nombres. Le plus grand facteur commun (GCF) de deux nombres est le plus grand nombre représentant un facteur des deux nombres. Voici comment trouver le GCF de 30 et de 36, en utilisant la factorisation en facteurs premiers:
1 Trouvez le plus grand facteur commun de deux nombres. Le plus grand facteur commun (GCF) de deux nombres est le plus grand nombre représentant un facteur des deux nombres. Voici comment trouver le GCF de 30 et de 36, en utilisant la factorisation en facteurs premiers: 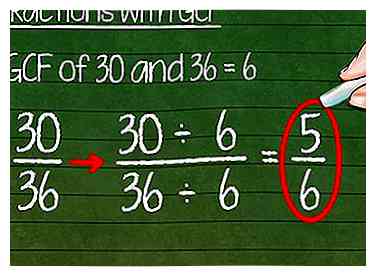 2 Simplifiez les fractions avec le GCF. Utilisez le facteur le plus commun chaque fois que vous pensez qu'une fraction n'est pas la plus simple. Trouvez le GCF du numérateur et du dénominateur, en utilisant le processus ci-dessus.Une fois que vous l'avez trouvé, divisez les deux parties de la fraction par le GCF.[3] La réponse sera la même fraction dans la forme la plus simple.
2 Simplifiez les fractions avec le GCF. Utilisez le facteur le plus commun chaque fois que vous pensez qu'une fraction n'est pas la plus simple. Trouvez le GCF du numérateur et du dénominateur, en utilisant le processus ci-dessus.Une fois que vous l'avez trouvé, divisez les deux parties de la fraction par le GCF.[3] La réponse sera la même fraction dans la forme la plus simple.  3 Trouvez le plus petit multiple commun de deux nombres. Le plus petit multiple commun (LCM) de deux nombres est le plus petit nombre qui a les deux premiers nombres comme facteurs. Par exemple, le LCM de 2 et 3 est 6, car les deux facteurs sont 2 et 3. Voici un exemple de recherche de LCM à partir de la factorisation:
3 Trouvez le plus petit multiple commun de deux nombres. Le plus petit multiple commun (LCM) de deux nombres est le plus petit nombre qui a les deux premiers nombres comme facteurs. Par exemple, le LCM de 2 et 3 est 6, car les deux facteurs sont 2 et 3. Voici un exemple de recherche de LCM à partir de la factorisation:  4 Utilisez le LCM pour ajouter des fractions. Avant de pouvoir ajouter deux fractions ensemble, leurs dénominateurs doivent être les mêmes. Trouvez le plus petit commun multiple des deux dénominateurs. Multipliez chaque fraction de sorte que le nouveau dénominateur soit le LCM. Une fois que les deux fractions sont dans cette forme, vous pouvez les ajouter ensemble.
4 Utilisez le LCM pour ajouter des fractions. Avant de pouvoir ajouter deux fractions ensemble, leurs dénominateurs doivent être les mêmes. Trouvez le plus petit commun multiple des deux dénominateurs. Multipliez chaque fraction de sorte que le nouveau dénominateur soit le LCM. Une fois que les deux fractions sont dans cette forme, vous pouvez les ajouter ensemble.