Le plus grand commun diviseur (GCD) de deux nombres entiers, également appelé le plus grand facteur commun (GCF) et le facteur le plus élevé commun (HCF), est le plus grand nombre entier qui est un diviseur (facteur) de chacun d'eux. Par exemple, le plus grand nombre qui se divise à la fois en 20 et 16 est 4. (les deux 16 et 20 ont des facteurs plus importants, mais pas plus commun facteurs - par exemple, 8 est un facteur de 16, mais ce n’est pas un facteur de 20.) Au niveau de l’école primaire, la plupart des gens apprennent une méthode de recherche et d’évaluation. Au lieu de cela, il existe un moyen simple et systématique de le faire qui conduit toujours à la bonne réponse. La méthode s'appelle "l'algorithme d'Euclid". Si vous voulez savoir comment trouver le plus grand commun diviseur de deux nombres entiers, voir l'étape 1 pour commencer.
Méthode One of Two:
Utilisation de l'algorithme de diviseur
-
 1 Supprimez tous les signes négatifs.
1 Supprimez tous les signes négatifs. -
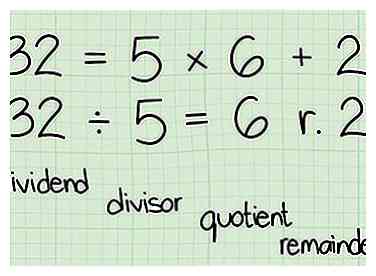 2 Connaissez votre vocabulaire: quand on divise 32 par 5,
2 Connaissez votre vocabulaire: quand on divise 32 par 5, -
- 32 est le dividende
- 5 est le diviseur
- 6 est le quotient
- 2 est le reste (ou modulo).
-
-
 3 Identifiez le plus grand des deux nombres. Ce sera le dividende, et plus le diviseur sera petit.
3 Identifiez le plus grand des deux nombres. Ce sera le dividende, et plus le diviseur sera petit. -
 4 Écrivez cet algorithme: (dividende) = (diviseur) * (quotient) + (reste)
4 Écrivez cet algorithme: (dividende) = (diviseur) * (quotient) + (reste) -
 5 Mettez le plus grand nombre au comptant pour le dividende et le plus petit nombre comme diviseur.
5 Mettez le plus grand nombre au comptant pour le dividende et le plus petit nombre comme diviseur. -
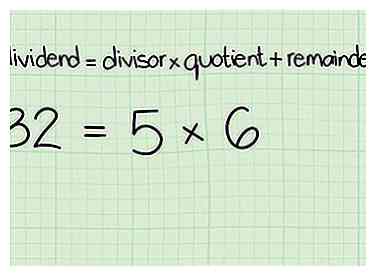 6 Décidez combien de fois le plus petit nombre se divisera dans le plus grand nombre et déposez-le dans l'algorithme en tant que quotient.
6 Décidez combien de fois le plus petit nombre se divisera dans le plus grand nombre et déposez-le dans l'algorithme en tant que quotient. -
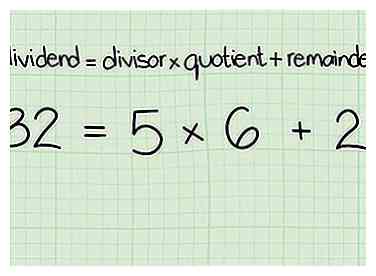 7 Calculez le reste et remplacez-le à l'endroit approprié dans l'algorithme.
7 Calculez le reste et remplacez-le à l'endroit approprié dans l'algorithme. -
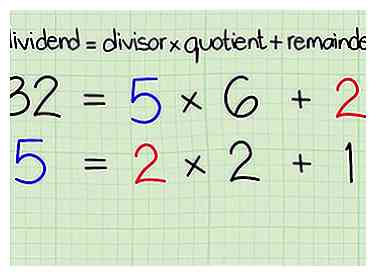 8 Ecrire l'algorithme à nouveau, mais cette fois-ci A) utiliser l'ancien diviseur comme nouveau dividende et B) utiliser le reste comme nouveau diviseur.
8 Ecrire l'algorithme à nouveau, mais cette fois-ci A) utiliser l'ancien diviseur comme nouveau dividende et B) utiliser le reste comme nouveau diviseur. -
 9 Répétez l'étape précédente jusqu'à ce que le reste soit égal à zéro.
9 Répétez l'étape précédente jusqu'à ce que le reste soit égal à zéro. -
 10 Le dernier diviseur est le plus grand diviseur commun.
10 Le dernier diviseur est le plus grand diviseur commun. -
 11 Voici un exemple où nous essayons de trouver le GCD de 108 et 30:
11 Voici un exemple où nous essayons de trouver le GCD de 108 et 30: -
 12 Remarquez comment les 30 et les 18 dans la première ligne changent de position pour créer la deuxième ligne. Ensuite, les 18 et 12 décalent pour créer la troisième ligne et les décalages 12 et 6 pour créer la quatrième ligne. Les 3, 1, 1 et 2 qui suivent le symbole de multiplication ne réapparaissent pas. Ils représentent combien de fois le diviseur entre dans le dividende, ils sont donc uniques à chaque ligne.
12 Remarquez comment les 30 et les 18 dans la première ligne changent de position pour créer la deuxième ligne. Ensuite, les 18 et 12 décalent pour créer la troisième ligne et les décalages 12 et 6 pour créer la quatrième ligne. Les 3, 1, 1 et 2 qui suivent le symbole de multiplication ne réapparaissent pas. Ils représentent combien de fois le diviseur entre dans le dividende, ils sont donc uniques à chaque ligne.
Méthode deux sur deux:
Utilisation de facteurs premiers
-
 1 Supprimez tous les signes négatifs.
1 Supprimez tous les signes négatifs. -
 2 Trouvez la factorisation en nombres premiers des nombres et listez-les comme indiqué.
2 Trouvez la factorisation en nombres premiers des nombres et listez-les comme indiqué. - En utilisant 24 et 18 comme exemples de nombres:
- 24- 2 x 2 x 2 x 3
- 18- 2 x 3 x 3
- En utilisant 50 et 35 comme numéros d’exemple:
- 50- 2 x 5 x 5
- 35- 5 x 7
- En utilisant 24 et 18 comme exemples de nombres:
-
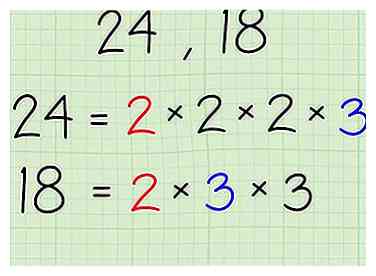 3 Identifier tous les facteurs premiers communs.
3 Identifier tous les facteurs premiers communs. - En utilisant 24 et 18 comme exemples de nombres:
- 24- 2 x 2 x 2 x 3
- 18- 2 X 3 x 3
- En utilisant 50 et 35 comme numéros d’exemple:
- 50- 2 x 5 x 5
- 35- 5 x 7
- En utilisant 24 et 18 comme exemples de nombres:
-
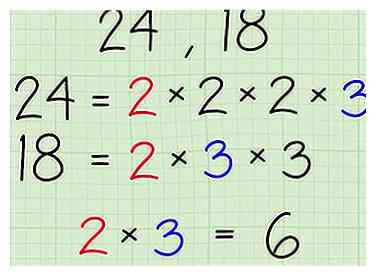 4 Multipliez les facteurs communs ensemble.
4 Multipliez les facteurs communs ensemble. - En cas de 24 et 18, multiplier 2 et 3 ensemble pour obtenir 6. Six est le plus grand facteur commun de 24 et 18.
- Dans le cas des 50 et 35, il n'y a rien à multiplier. 5 est le seul facteur commun, et donc le plus grand.
-
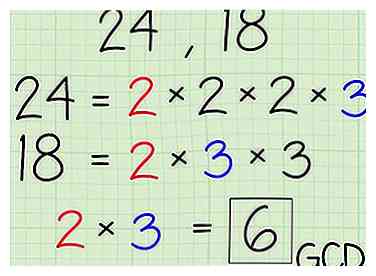 5 Fini.
5 Fini.
 Minotauromaquia
Minotauromaquia
 1 Supprimez tous les signes négatifs.
1 Supprimez tous les signes négatifs. 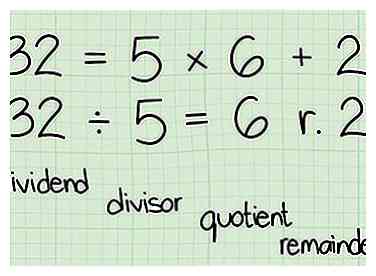 2 Connaissez votre vocabulaire: quand on divise 32 par 5,
2 Connaissez votre vocabulaire: quand on divise 32 par 5,  3 Identifiez le plus grand des deux nombres. Ce sera le dividende, et plus le diviseur sera petit.
3 Identifiez le plus grand des deux nombres. Ce sera le dividende, et plus le diviseur sera petit.  4 Écrivez cet algorithme: (dividende) = (diviseur) * (quotient) + (reste)
4 Écrivez cet algorithme: (dividende) = (diviseur) * (quotient) + (reste)  5 Mettez le plus grand nombre au comptant pour le dividende et le plus petit nombre comme diviseur.
5 Mettez le plus grand nombre au comptant pour le dividende et le plus petit nombre comme diviseur. 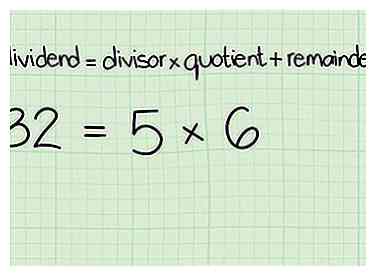 6 Décidez combien de fois le plus petit nombre se divisera dans le plus grand nombre et déposez-le dans l'algorithme en tant que quotient.
6 Décidez combien de fois le plus petit nombre se divisera dans le plus grand nombre et déposez-le dans l'algorithme en tant que quotient. 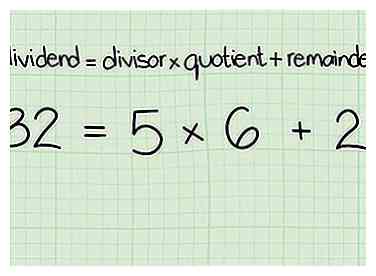 7 Calculez le reste et remplacez-le à l'endroit approprié dans l'algorithme.
7 Calculez le reste et remplacez-le à l'endroit approprié dans l'algorithme. 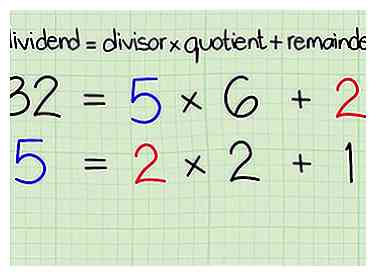 8 Ecrire l'algorithme à nouveau, mais cette fois-ci A) utiliser l'ancien diviseur comme nouveau dividende et B) utiliser le reste comme nouveau diviseur.
8 Ecrire l'algorithme à nouveau, mais cette fois-ci A) utiliser l'ancien diviseur comme nouveau dividende et B) utiliser le reste comme nouveau diviseur.  9 Répétez l'étape précédente jusqu'à ce que le reste soit égal à zéro.
9 Répétez l'étape précédente jusqu'à ce que le reste soit égal à zéro.  10 Le dernier diviseur est le plus grand diviseur commun.
10 Le dernier diviseur est le plus grand diviseur commun.  11 Voici un exemple où nous essayons de trouver le GCD de 108 et 30:
11 Voici un exemple où nous essayons de trouver le GCD de 108 et 30:  12 Remarquez comment les 30 et les 18 dans la première ligne changent de position pour créer la deuxième ligne. Ensuite, les 18 et 12 décalent pour créer la troisième ligne et les décalages 12 et 6 pour créer la quatrième ligne. Les 3, 1, 1 et 2 qui suivent le symbole de multiplication ne réapparaissent pas. Ils représentent combien de fois le diviseur entre dans le dividende, ils sont donc uniques à chaque ligne.
12 Remarquez comment les 30 et les 18 dans la première ligne changent de position pour créer la deuxième ligne. Ensuite, les 18 et 12 décalent pour créer la troisième ligne et les décalages 12 et 6 pour créer la quatrième ligne. Les 3, 1, 1 et 2 qui suivent le symbole de multiplication ne réapparaissent pas. Ils représentent combien de fois le diviseur entre dans le dividende, ils sont donc uniques à chaque ligne.  1 Supprimez tous les signes négatifs.
1 Supprimez tous les signes négatifs.  2 Trouvez la factorisation en nombres premiers des nombres et listez-les comme indiqué.
2 Trouvez la factorisation en nombres premiers des nombres et listez-les comme indiqué. 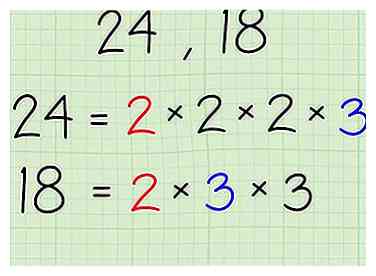 3 Identifier tous les facteurs premiers communs.
3 Identifier tous les facteurs premiers communs. 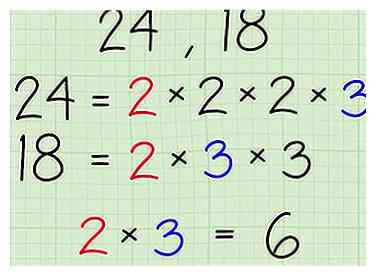 4 Multipliez les facteurs communs ensemble.
4 Multipliez les facteurs communs ensemble. 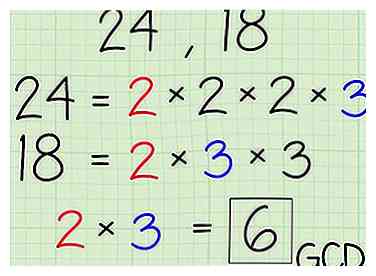 5 Fini.
5 Fini.