Les entiers sont des nombres entiers positifs ou négatifs sans composante décimale ou fractionnaire. Multiplier et diviser deux nombres entiers ou plus n'est pas très différent de la multiplication et de la division des nombres entiers de base. La principale différence réside dans le fait que certains entiers étant négatifs, vous devez garder une trace de leurs signes. En prenant en compte les signes de vos entiers, vous pouvez procéder en multipliant comme d'habitude.
Pas
Informations générales
-
 1 Connaissez vos nombres entiers. Un entier est tout nombre entier pouvant être représenté sans utiliser de fraction ou de décimal. Les nombres entiers peuvent être positifs, négatifs ou nuls. Par exemple, les nombres suivants sont des nombres entiers: 1, 99, -217 et 0. Cependant, ces nombres ne sont pas: -10.4, 6 ¾, 2.12.
1 Connaissez vos nombres entiers. Un entier est tout nombre entier pouvant être représenté sans utiliser de fraction ou de décimal. Les nombres entiers peuvent être positifs, négatifs ou nuls. Par exemple, les nombres suivants sont des nombres entiers: 1, 99, -217 et 0. Cependant, ces nombres ne sont pas: -10.4, 6 ¾, 2.12. - Les valeurs absolues peuvent être des entiers, mais elles ne le sont pas nécessairement. La valeur absolue d'un nombre est la "taille" ou le "montant" du nombre, quel que soit son signe. Une autre façon de le dire est que la valeur absolue d'un nombre donné est la distance de ce nombre par rapport à zéro. Ainsi, la valeur absolue d'un entier est toujours un entier. Par exemple, la valeur absolue de -12 est 12. La valeur absolue de 3 est 3. La valeur absolue de 0 est 0.
- Les valeurs absolues des nombres qui ne sont pas des entiers ne seront toutefois jamais des entiers. Par exemple, la valeur absolue de 1/11 est 1/11 - une fraction, et donc pas un entier.
- Les valeurs absolues peuvent être des entiers, mais elles ne le sont pas nécessairement. La valeur absolue d'un nombre est la "taille" ou le "montant" du nombre, quel que soit son signe. Une autre façon de le dire est que la valeur absolue d'un nombre donné est la distance de ce nombre par rapport à zéro. Ainsi, la valeur absolue d'un entier est toujours un entier. Par exemple, la valeur absolue de -12 est 12. La valeur absolue de 3 est 3. La valeur absolue de 0 est 0.
- 2 Connaissez vos horaires de base. Le processus de multiplication ou de division des nombres entiers, qu'ils soient grands ou petits, est beaucoup plus rapide et facile si vous avez mémorisé les produits de chaque paire de numéros de 1 à 10. Cette information est généralement appelée à l'école "fois les tables". En guise de rappel, vous trouverez ci-dessous un tableau de base 10X10. Les nombres situés en haut et à gauche du tableau indiquent les nombres de 1 à 10. Pour trouver le produit de deux de ces numéros, recherchez la cellule où se croisent la ligne et la colonne de vos deux nombres souhaités:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |

Méthode One of Two:
Multiplier les entiers
-
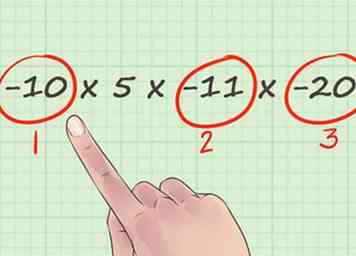 1 Comptez le nombre de signes négatifs dans votre problème de multiplication. Un problème de multiplication de base entre deux nombres positifs ou plus entraînera toujours une réponse positive. Cependant, chaque signe négatif ajouté à un problème de multiplication retourne le signe du positif au négatif ou vice versa. Pour commencer un problème de multiplication d'entiers, comptez le nombre de signes négatifs dans le problème.
1 Comptez le nombre de signes négatifs dans votre problème de multiplication. Un problème de multiplication de base entre deux nombres positifs ou plus entraînera toujours une réponse positive. Cependant, chaque signe négatif ajouté à un problème de multiplication retourne le signe du positif au négatif ou vice versa. Pour commencer un problème de multiplication d'entiers, comptez le nombre de signes négatifs dans le problème. - Utilisons l'exemple du problème -10 × 5 × -11 × -20. Dans ce problème, nous pouvons clairement voir Trois signes négatifs. Nous utiliserons ces informations à l'étape suivante.
-
 2 Décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Comme indiqué ci-dessus, la réponse à un problème de multiplication impliquant uniquement des nombres entiers positifs sera positive. Pour chaque signe négatif négatif dans votre problème, retournez le signe de votre réponse. En d'autres termes, si votre problème a un signe négatif, votre réponse sera négative; si elle en a deux, votre réponse sera positive, etc. Une bonne règle de base est que nombres impairs de signes négatifs donner des réponses négatives et nombre pair de signes négatifs donner des réponses positives.
2 Décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Comme indiqué ci-dessus, la réponse à un problème de multiplication impliquant uniquement des nombres entiers positifs sera positive. Pour chaque signe négatif négatif dans votre problème, retournez le signe de votre réponse. En d'autres termes, si votre problème a un signe négatif, votre réponse sera négative; si elle en a deux, votre réponse sera positive, etc. Une bonne règle de base est que nombres impairs de signes négatifs donner des réponses négatives et nombre pair de signes négatifs donner des réponses positives. - Dans notre exemple, nous avons trois signes négatifs. Trois est un nombre impair, donc nous savons que notre réponse est négatif. Nous pouvons mettre un signe négatif dans l'espace pour notre réponse, comme ceci: -10 × 5 × -11 × -20 = -__
-
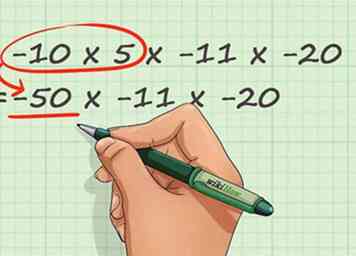 3 Multipliez les nombres de 1 à 10 en utilisant les connaissances de base des temps. Le produit de deux nombres inférieurs ou égaux à 10 est couvert dans les tableaux chronologiques de base (voir ci-dessus). Pour ces cas simples, écrivez simplement la réponse. Rappelez-vous que, dans les problèmes qui utilisent uniquement des signes de multiplication, vous pouvez déplacer les entiers afin de pouvoir multiplier des nombres simples les uns avec les autres.
3 Multipliez les nombres de 1 à 10 en utilisant les connaissances de base des temps. Le produit de deux nombres inférieurs ou égaux à 10 est couvert dans les tableaux chronologiques de base (voir ci-dessus). Pour ces cas simples, écrivez simplement la réponse. Rappelez-vous que, dans les problèmes qui utilisent uniquement des signes de multiplication, vous pouvez déplacer les entiers afin de pouvoir multiplier des nombres simples les uns avec les autres. - Dans notre exemple, 10 × 5 est couvert dans le tableau des temps de base. Nous n'avons pas à tenir compte du signe négatif sur les dix parce que nous avons déjà trouvé le signe de notre réponse. 10 × 5 = 50. Nous pouvons insérer ceci dans notre problème comme ceci: (50) × -11 × -20 = -__
- Si vous rencontrez des difficultés pour visualiser les problèmes de multiplication de base, pensez à ceux-ci en termes de problèmes d’ajout. Par exemple, 5 × 10 est comme dire "cinq, dix fois". En d'autres termes, 5 × 10 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5.
- Dans notre exemple, 10 × 5 est couvert dans le tableau des temps de base. Nous n'avons pas à tenir compte du signe négatif sur les dix parce que nous avons déjà trouvé le signe de notre réponse. 10 × 5 = 50. Nous pouvons insérer ceci dans notre problème comme ceci: (50) × -11 × -20 = -__
-
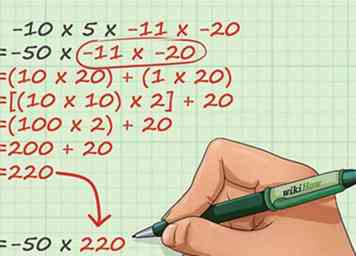 4 Si nécessaire, divisez les grands nombres en morceaux maniables. Si votre problème de multiplication implique des nombres supérieurs à dix, vous ne devez pas nécessairement utiliser une multiplication longue. D'abord, voyez si vous pouvez diviser un ou plusieurs de vos nombres en morceaux plus petits et plus faciles à utiliser. Comme, avec les connaissances de base sur les tables de temps, vous pouvez résoudre des problèmes de multiplication simples presque instantanément, il est généralement plus simple de résoudre un problème difficile que de résoudre un problème difficile.
4 Si nécessaire, divisez les grands nombres en morceaux maniables. Si votre problème de multiplication implique des nombres supérieurs à dix, vous ne devez pas nécessairement utiliser une multiplication longue. D'abord, voyez si vous pouvez diviser un ou plusieurs de vos nombres en morceaux plus petits et plus faciles à utiliser. Comme, avec les connaissances de base sur les tables de temps, vous pouvez résoudre des problèmes de multiplication simples presque instantanément, il est généralement plus simple de résoudre un problème difficile que de résoudre un problème difficile. - Regardons la seconde moitié de notre exemple de problème, -11 × -20. Nous pouvons omettre les signes car nous avons déjà compris le signe de notre réponse. 11 × 20 semble intimidant, mais si nous réécrivons le problème sous la forme 10 × 20 + 1 × 20, soudain, c'est beaucoup plus facile à gérer. 10 × 20 est juste 2 fois 10 × 10, ou 200. 1 × 20 est juste 20. En additionnant nos réponses, nous obtenons 200 + 20 = 220. Nous pouvons réinsérer ceci dans notre problème comme suit: (50) × (220) = -__
-
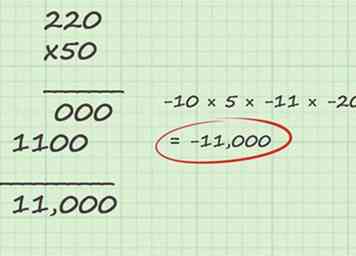 5 Pour les nombres plus difficiles, utilisez une multiplication longue. Si votre problème de multiplication implique deux nombres ou plus supérieurs à 10 et que vous ne parvenez pas à trouver la réponse en divisant votre problème en morceaux exploitables, vous pouvez toujours résoudre le problème par une multiplication longue.En cas de multiplication longue, vous alignez vos réponses comme vous le feriez dans un problème d’ajout et multiplions chaque chiffre du nombre inférieur par chaque chiffre du numéro supérieur. Si le nombre inférieur comporte plus d'un chiffre, vous devez tenir compte des chiffres des dizaines, des centaines et ainsi de suite en ajoutant des zéros à droite de votre réponse partielle. Enfin, pour obtenir votre réponse finale, additionnez toutes les réponses partielles.
5 Pour les nombres plus difficiles, utilisez une multiplication longue. Si votre problème de multiplication implique deux nombres ou plus supérieurs à 10 et que vous ne parvenez pas à trouver la réponse en divisant votre problème en morceaux exploitables, vous pouvez toujours résoudre le problème par une multiplication longue.En cas de multiplication longue, vous alignez vos réponses comme vous le feriez dans un problème d’ajout et multiplions chaque chiffre du nombre inférieur par chaque chiffre du numéro supérieur. Si le nombre inférieur comporte plus d'un chiffre, vous devez tenir compte des chiffres des dizaines, des centaines et ainsi de suite en ajoutant des zéros à droite de votre réponse partielle. Enfin, pour obtenir votre réponse finale, additionnez toutes les réponses partielles. - Revenons à notre problème d'exemple. Maintenant, nous devons multiplier 50 par 220. Ce sera difficile de diviser en gros morceaux, utilisons donc une longue multiplication. Les problèmes de multiplication longs sont plus faciles à suivre si le plus petit nombre est en bas, écrivons donc notre problème avec 220 en haut et 50 en bas.
- Multipliez d'abord le chiffre à la place du nombre inférieur par chaque chiffre du numéro supérieur. Puisque 50 est en bas, 0 est le chiffre à la place. 0 × 0 est 0, 0 × 2 est 0 et 0 × 2 est zéro. En d'autres termes, 0 × 220 est égal à zéro. Notez ceci sous votre long problème de multiplication à la place de chacun. C'est notre première réponse partielle.
- Ensuite, nous multiplions le chiffre à la dixième place de notre nombre inférieur par chaque chiffre du numéro supérieur. 5 est le chiffre à la place des dizaines de 50. Comme il s'agit de 5 à la place des dizaines, nous écrivons un zéro au-dessous de notre première réponse partielle à la place avant de continuer. Ensuite, nous nous multiplions. 5 × 0 est 0. 5 × 2 est 10, alors écrivez 0 et ajoutez-en un au produit de 5 et au chiffre suivant. 5 × 2 est 10. Normalement, nous écririons 0 et porterions le 1, mais dans ce cas nous ajoutons également le 1 du problème précédent, ce qui nous donne 11. Écrivez "1". En portant le 1 à la place des dizaines de 11, nous voyons que nous sommes à court de chiffres, donc nous écrivons juste à gauche de notre réponse partielle jusqu'à présent. En enregistrant tout cela, il nous reste 11 000.
- Ensuite, nous venons d'ajouter. 0 + 11 000 est 11 000. Puisque nous savons que la réponse à notre problème initial est négative, nous pouvons affirmer que -10 × 5 × -11 × -20 = -11,000.
- Revenons à notre problème d'exemple. Maintenant, nous devons multiplier 50 par 220. Ce sera difficile de diviser en gros morceaux, utilisons donc une longue multiplication. Les problèmes de multiplication longs sont plus faciles à suivre si le plus petit nombre est en bas, écrivons donc notre problème avec 220 en haut et 50 en bas.
Méthode deux sur deux:
Division des nombres entiers
-
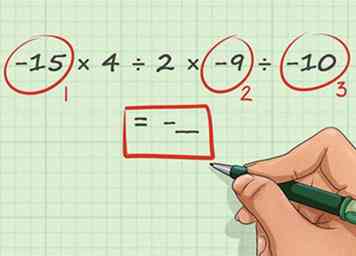 1 Comme précédemment, décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Introduire la division dans un problème mathématique ne change pas les règles concernant les signes négatifs. S'il y a un nombre impair de signes négatifs, la réponse est négative, alors que s'il y a un nombre pair de signes négatifs (ou pas du tout), la réponse sera positive.
1 Comme précédemment, décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Introduire la division dans un problème mathématique ne change pas les règles concernant les signes négatifs. S'il y a un nombre impair de signes négatifs, la réponse est négative, alors que s'il y a un nombre pair de signes négatifs (ou pas du tout), la réponse sera positive. - Utilisons un exemple de problème avec la multiplication et la division. Dans le problème -15 × 4 ÷ 2 × -9 ÷ -10, il y a trois signes négatifs, donc la réponse sera négatif. Comme précédemment, nous pouvons mettre un signe négatif dans l'espace pour notre réponse, comme ceci: -15 × 4 ÷ 2 × -9 ÷ -10 = -__
-
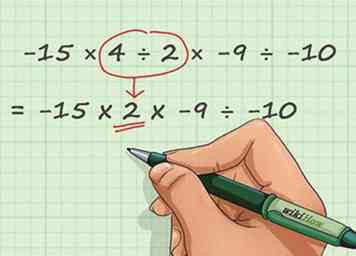 2 Faites des divisions simples en utilisant votre connaissance de la multiplication. La division peut être considérée comme une multiplication à rebours. Lorsque vous divisez un nombre par un autre, vous demandez de manière détournée: "combien de fois le deuxième nombre correspond-il au premier?" ou, en d'autres termes, "qu'est-ce que je dois multiplier par le deuxième nombre pour obtenir le premier?" Voir le tableau de base 10 x 10 fois pour référence - si on vous demande de diviser l’un des réponses dans le tableau des temps par un nombre quelconque n de 1 à 10, vous saurez que la réponse est juste l'autre chiffre de 1 à 10 nécessaire pour se multiplier n pour l'obtenir.
2 Faites des divisions simples en utilisant votre connaissance de la multiplication. La division peut être considérée comme une multiplication à rebours. Lorsque vous divisez un nombre par un autre, vous demandez de manière détournée: "combien de fois le deuxième nombre correspond-il au premier?" ou, en d'autres termes, "qu'est-ce que je dois multiplier par le deuxième nombre pour obtenir le premier?" Voir le tableau de base 10 x 10 fois pour référence - si on vous demande de diviser l’un des réponses dans le tableau des temps par un nombre quelconque n de 1 à 10, vous saurez que la réponse est juste l'autre chiffre de 1 à 10 nécessaire pour se multiplier n pour l'obtenir. - Regardons notre exemple de problème. Dans -15 × 4 ÷ 2 × -9 ÷ -10, nous voyons 4 ÷ 2. 4 est une réponse dans le tableau des temps - 4 × 1 et 2 × 2 donnent 4 comme réponse. Comme on nous demande de diviser 4 par 2, nous savons que nous résolvons essentiellement le problème 2 × __ = 4. Bien entendu, dans l'espace vide, nous écririons 2, donc 4 ÷ 2 = 2. Réécrivons notre problème comme -15 × (2) × -9 ÷ -10.
-
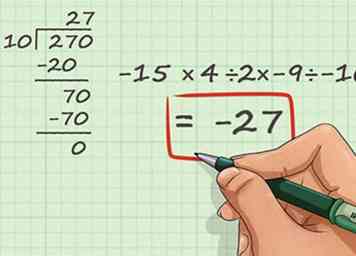 3 Utilisez une division longue si nécessaire. Comme avec la multiplication, lorsque vous rencontrez un problème de division trop difficile à résoudre mentalement ou avec un tableau des temps, vous avez la possibilité de résoudre avec une approche longue durée. Dans un problème de longue division, vous écrivez vos deux nombres dans une parenthèse spéciale en forme de L, puis divisez le chiffre par des chiffres et déplacez vos réponses partielles vers la droite pour tenir compte de la valeur décroissante des chiffres que vous avez. diviser - des centaines, puis des dizaines, puis des uns et ainsi de suite.
3 Utilisez une division longue si nécessaire. Comme avec la multiplication, lorsque vous rencontrez un problème de division trop difficile à résoudre mentalement ou avec un tableau des temps, vous avez la possibilité de résoudre avec une approche longue durée. Dans un problème de longue division, vous écrivez vos deux nombres dans une parenthèse spéciale en forme de L, puis divisez le chiffre par des chiffres et déplacez vos réponses partielles vers la droite pour tenir compte de la valeur décroissante des chiffres que vous avez. diviser - des centaines, puis des dizaines, puis des uns et ainsi de suite. - Utilisons la division longue dans notre exemple de problème. Nous pouvons simplifier -15 × (2) × -9 ÷ -10 à 270 ÷ -10. Nous ignorerons les signes comme d'habitude car nous connaissons le signe de notre réponse finale. Écrivez 10 à gauche du support en forme de L et écrivez 270 en dessous.
- Nous commençons par diviser le premier chiffre du nombre sous le crochet par le nombre sur le côté. Le premier chiffre est 2 et notre numéro sur le côté est 10. Comme 10 ne correspond pas à deux, nous utiliserons plutôt les deux premiers chiffres. dix Est-ce que adapter en 27 - il tient dans deux fois. Écrivez "2" au-dessus du 7 sous le crochet. 2 est le premier chiffre de votre réponse.
- Ensuite, multipliez le nombre à gauche du crochet par le chiffre que vous venez de découvrir. 2 × 10 est 20. Écrivez ceci sous les deux premiers chiffres du nombre sous le crochet - dans ce cas, 2 et 7.
- Soustrayez les chiffres que vous venez d'écrire. 27 moins 20 est 7. Écrivez ceci au fond de votre problème croissant.
- Abaissez le chiffre suivant du numéro sous le crochet. Ce chiffre suivant de 270 est 0. Laissez-le tomber à côté du 7 pour faire 70.
- Divisez votre nouveau numéro. Ensuite, divisez 10 en 70. 10 correspond exactement à 7 fois en 70, alors écrivez en haut à côté de 2. Ceci est le deuxième chiffre de votre réponse. Votre réponse finale est 27.
- Notez que, dans le cas où 10 n'a pas diviser uniformément dans notre nombre final, nous devrions tenir compte de la quantité de 10 qui reste - le reste. Par exemple, si notre dernier acte était de diviser 71, au lieu de 70, de 10, nous remarquerions que 10 ne correspond pas exactement à 71. Cela correspond à 7 fois, mais il en reste 1. En d'autres termes, nous pouvons adapter sept 10 et un supplémentaire sur 71. Nous écririons notre réponse, alors, comme "27 restants 1" ou "27 r1".
- Utilisons la division longue dans notre exemple de problème. Nous pouvons simplifier -15 × (2) × -9 ÷ -10 à 270 ÷ -10. Nous ignorerons les signes comme d'habitude car nous connaissons le signe de notre réponse finale. Écrivez 10 à gauche du support en forme de L et écrivez 270 en dessous.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Connaissez vos nombres entiers. Un entier est tout nombre entier pouvant être représenté sans utiliser de fraction ou de décimal. Les nombres entiers peuvent être positifs, négatifs ou nuls. Par exemple, les nombres suivants sont des nombres entiers: 1, 99, -217 et 0. Cependant, ces nombres ne sont pas: -10.4, 6 ¾, 2.12.
1 Connaissez vos nombres entiers. Un entier est tout nombre entier pouvant être représenté sans utiliser de fraction ou de décimal. Les nombres entiers peuvent être positifs, négatifs ou nuls. Par exemple, les nombres suivants sont des nombres entiers: 1, 99, -217 et 0. Cependant, ces nombres ne sont pas: -10.4, 6 ¾, 2.12. 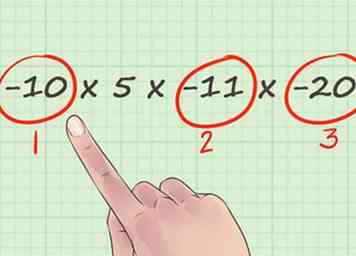 1 Comptez le nombre de signes négatifs dans votre problème de multiplication. Un problème de multiplication de base entre deux nombres positifs ou plus entraînera toujours une réponse positive. Cependant, chaque signe négatif ajouté à un problème de multiplication retourne le signe du positif au négatif ou vice versa. Pour commencer un problème de multiplication d'entiers, comptez le nombre de signes négatifs dans le problème.
1 Comptez le nombre de signes négatifs dans votre problème de multiplication. Un problème de multiplication de base entre deux nombres positifs ou plus entraînera toujours une réponse positive. Cependant, chaque signe négatif ajouté à un problème de multiplication retourne le signe du positif au négatif ou vice versa. Pour commencer un problème de multiplication d'entiers, comptez le nombre de signes négatifs dans le problème.  2 Décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Comme indiqué ci-dessus, la réponse à un problème de multiplication impliquant uniquement des nombres entiers positifs sera positive. Pour chaque signe négatif négatif dans votre problème, retournez le signe de votre réponse. En d'autres termes, si votre problème a un signe négatif, votre réponse sera négative; si elle en a deux, votre réponse sera positive, etc. Une bonne règle de base est que nombres impairs de signes négatifs donner des réponses négatives et nombre pair de signes négatifs donner des réponses positives.
2 Décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Comme indiqué ci-dessus, la réponse à un problème de multiplication impliquant uniquement des nombres entiers positifs sera positive. Pour chaque signe négatif négatif dans votre problème, retournez le signe de votre réponse. En d'autres termes, si votre problème a un signe négatif, votre réponse sera négative; si elle en a deux, votre réponse sera positive, etc. Une bonne règle de base est que nombres impairs de signes négatifs donner des réponses négatives et nombre pair de signes négatifs donner des réponses positives. 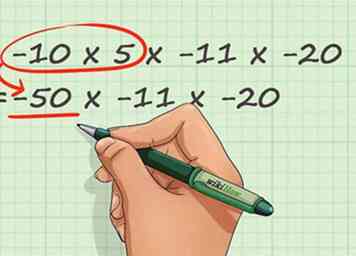 3 Multipliez les nombres de 1 à 10 en utilisant les connaissances de base des temps. Le produit de deux nombres inférieurs ou égaux à 10 est couvert dans les tableaux chronologiques de base (voir ci-dessus). Pour ces cas simples, écrivez simplement la réponse. Rappelez-vous que, dans les problèmes qui utilisent uniquement des signes de multiplication, vous pouvez déplacer les entiers afin de pouvoir multiplier des nombres simples les uns avec les autres.
3 Multipliez les nombres de 1 à 10 en utilisant les connaissances de base des temps. Le produit de deux nombres inférieurs ou égaux à 10 est couvert dans les tableaux chronologiques de base (voir ci-dessus). Pour ces cas simples, écrivez simplement la réponse. Rappelez-vous que, dans les problèmes qui utilisent uniquement des signes de multiplication, vous pouvez déplacer les entiers afin de pouvoir multiplier des nombres simples les uns avec les autres. 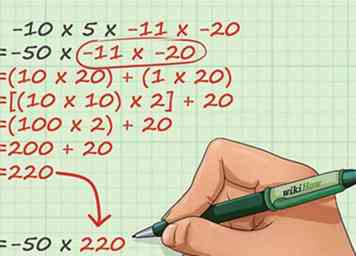 4 Si nécessaire, divisez les grands nombres en morceaux maniables. Si votre problème de multiplication implique des nombres supérieurs à dix, vous ne devez pas nécessairement utiliser une multiplication longue. D'abord, voyez si vous pouvez diviser un ou plusieurs de vos nombres en morceaux plus petits et plus faciles à utiliser. Comme, avec les connaissances de base sur les tables de temps, vous pouvez résoudre des problèmes de multiplication simples presque instantanément, il est généralement plus simple de résoudre un problème difficile que de résoudre un problème difficile.
4 Si nécessaire, divisez les grands nombres en morceaux maniables. Si votre problème de multiplication implique des nombres supérieurs à dix, vous ne devez pas nécessairement utiliser une multiplication longue. D'abord, voyez si vous pouvez diviser un ou plusieurs de vos nombres en morceaux plus petits et plus faciles à utiliser. Comme, avec les connaissances de base sur les tables de temps, vous pouvez résoudre des problèmes de multiplication simples presque instantanément, il est généralement plus simple de résoudre un problème difficile que de résoudre un problème difficile. 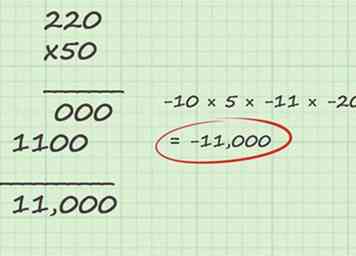 5 Pour les nombres plus difficiles, utilisez une multiplication longue. Si votre problème de multiplication implique deux nombres ou plus supérieurs à 10 et que vous ne parvenez pas à trouver la réponse en divisant votre problème en morceaux exploitables, vous pouvez toujours résoudre le problème par une multiplication longue.En cas de multiplication longue, vous alignez vos réponses comme vous le feriez dans un problème d’ajout et multiplions chaque chiffre du nombre inférieur par chaque chiffre du numéro supérieur. Si le nombre inférieur comporte plus d'un chiffre, vous devez tenir compte des chiffres des dizaines, des centaines et ainsi de suite en ajoutant des zéros à droite de votre réponse partielle. Enfin, pour obtenir votre réponse finale, additionnez toutes les réponses partielles.
5 Pour les nombres plus difficiles, utilisez une multiplication longue. Si votre problème de multiplication implique deux nombres ou plus supérieurs à 10 et que vous ne parvenez pas à trouver la réponse en divisant votre problème en morceaux exploitables, vous pouvez toujours résoudre le problème par une multiplication longue.En cas de multiplication longue, vous alignez vos réponses comme vous le feriez dans un problème d’ajout et multiplions chaque chiffre du nombre inférieur par chaque chiffre du numéro supérieur. Si le nombre inférieur comporte plus d'un chiffre, vous devez tenir compte des chiffres des dizaines, des centaines et ainsi de suite en ajoutant des zéros à droite de votre réponse partielle. Enfin, pour obtenir votre réponse finale, additionnez toutes les réponses partielles. 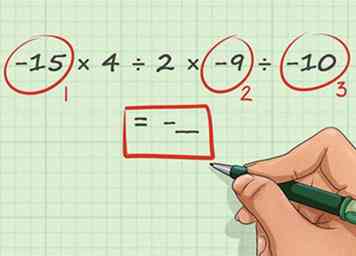 1 Comme précédemment, décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Introduire la division dans un problème mathématique ne change pas les règles concernant les signes négatifs. S'il y a un nombre impair de signes négatifs, la réponse est négative, alors que s'il y a un nombre pair de signes négatifs (ou pas du tout), la réponse sera positive.
1 Comme précédemment, décidez du signe de votre réponse en fonction du nombre de signes négatifs dans le problème. Introduire la division dans un problème mathématique ne change pas les règles concernant les signes négatifs. S'il y a un nombre impair de signes négatifs, la réponse est négative, alors que s'il y a un nombre pair de signes négatifs (ou pas du tout), la réponse sera positive. 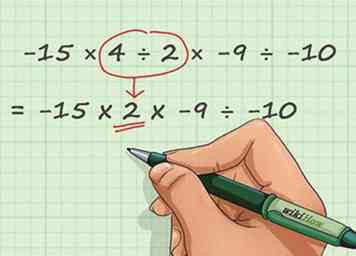 2 Faites des divisions simples en utilisant votre connaissance de la multiplication. La division peut être considérée comme une multiplication à rebours. Lorsque vous divisez un nombre par un autre, vous demandez de manière détournée: "combien de fois le deuxième nombre correspond-il au premier?" ou, en d'autres termes, "qu'est-ce que je dois multiplier par le deuxième nombre pour obtenir le premier?" Voir le tableau de base 10 x 10 fois pour référence - si on vous demande de diviser l’un des réponses dans le tableau des temps par un nombre quelconque n de 1 à 10, vous saurez que la réponse est juste l'autre chiffre de 1 à 10 nécessaire pour se multiplier n pour l'obtenir.
2 Faites des divisions simples en utilisant votre connaissance de la multiplication. La division peut être considérée comme une multiplication à rebours. Lorsque vous divisez un nombre par un autre, vous demandez de manière détournée: "combien de fois le deuxième nombre correspond-il au premier?" ou, en d'autres termes, "qu'est-ce que je dois multiplier par le deuxième nombre pour obtenir le premier?" Voir le tableau de base 10 x 10 fois pour référence - si on vous demande de diviser l’un des réponses dans le tableau des temps par un nombre quelconque n de 1 à 10, vous saurez que la réponse est juste l'autre chiffre de 1 à 10 nécessaire pour se multiplier n pour l'obtenir. 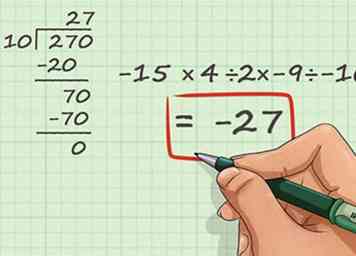 3 Utilisez une division longue si nécessaire. Comme avec la multiplication, lorsque vous rencontrez un problème de division trop difficile à résoudre mentalement ou avec un tableau des temps, vous avez la possibilité de résoudre avec une approche longue durée. Dans un problème de longue division, vous écrivez vos deux nombres dans une parenthèse spéciale en forme de L, puis divisez le chiffre par des chiffres et déplacez vos réponses partielles vers la droite pour tenir compte de la valeur décroissante des chiffres que vous avez. diviser - des centaines, puis des dizaines, puis des uns et ainsi de suite.
3 Utilisez une division longue si nécessaire. Comme avec la multiplication, lorsque vous rencontrez un problème de division trop difficile à résoudre mentalement ou avec un tableau des temps, vous avez la possibilité de résoudre avec une approche longue durée. Dans un problème de longue division, vous écrivez vos deux nombres dans une parenthèse spéciale en forme de L, puis divisez le chiffre par des chiffres et déplacez vos réponses partielles vers la droite pour tenir compte de la valeur décroissante des chiffres que vous avez. diviser - des centaines, puis des dizaines, puis des uns et ainsi de suite.