La multiplication des lignes est parfois appelée multiplication des bâtons, et ses origines ne sont pas claires, certaines sources prétendant qu'elles proviennent des Japonais,[1] Chinois,[2] ou cultures védiques.[3] C'est fondamentalement le même processus que l'algorithme de multiplication standard que l'on vous enseigne à l'école, sauf qu'il est représenté de manière plus visuelle. En utilisant l'intersection de lignes ou de bâtons pour représenter l'endroit où vous multipliez les différentes valeurs de lieu, cette méthode peut être utile pour les apprenants plus visuellement orientés.
Première partie de deux:
Mise en place du problème
-
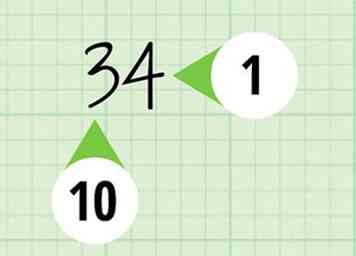 1 Déterminez les valeurs de position de votre premier numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit.
1 Déterminez les valeurs de position de votre premier numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit. - Par exemple, si vous multipliez , vous déterminez que le premier nombre, 34, a un 4 à la place et un 3 à la place des dizaines.
-
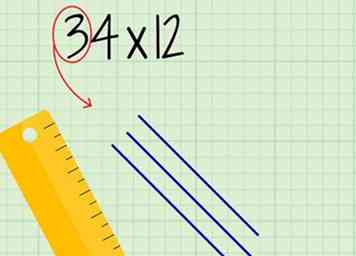 2 Tracez des lignes parallèles pour représenter la dizaine de votre premier numéro. Le nombre de lignes que vous dessinez correspondra au chiffre à la place des dizaines.
2 Tracez des lignes parallèles pour représenter la dizaine de votre premier numéro. Le nombre de lignes que vous dessinez correspondra au chiffre à la place des dizaines. - Tracez les lignes à un angle d’environ 45 degrés et inclinez-les vers la droite.
- Par exemple, si vous représentez 34, vous tracez 3 lignes parallèles.
-
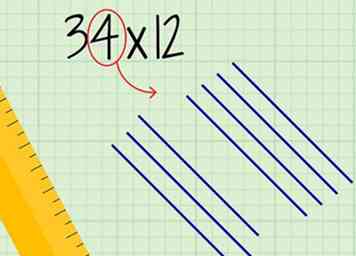 3 Tracez des lignes parallèles pour représenter le lieu de votre premier numéro. Le nombre de lignes correspondra au chiffre à la place. Dessinez ces lignes au-dessus et à droite des lignes de dizaines.
3 Tracez des lignes parallèles pour représenter le lieu de votre premier numéro. Le nombre de lignes correspondra au chiffre à la place. Dessinez ces lignes au-dessus et à droite des lignes de dizaines. - Laissez un espace entre les lignes et les lignes de dizaines, pour pouvoir les distinguer.
- Par exemple, si vous représentez 34, vous allez dessiner 4 lignes parallèles.
-
 4 Déterminez les valeurs de position de votre deuxième numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit.
4 Déterminez les valeurs de position de votre deuxième numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit. - Par exemple, si votre deuxième numéro est 12, vous déterminez que vous avez un 2 à la place et un 1 à la place des dizaines.
-
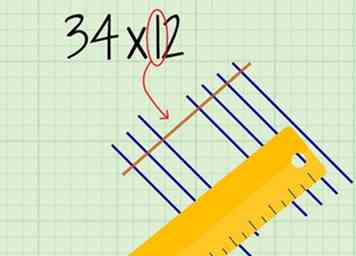 5 Tracez des lignes parallèles pour représenter la dizaine de votre deuxième nombre. Le nombre de lignes correspondra au chiffre à la place des dizaines. Tracez les lignes près du haut du diagramme. Ils devraient croiser toutes les lignes du premier nombre, en s'inclinant dans la direction opposée.
5 Tracez des lignes parallèles pour représenter la dizaine de votre deuxième nombre. Le nombre de lignes correspondra au chiffre à la place des dizaines. Tracez les lignes près du haut du diagramme. Ils devraient croiser toutes les lignes du premier nombre, en s'inclinant dans la direction opposée. - Il peut être utile de dessiner les lignes de chaque numéro dans une couleur différente.
- Par exemple, si vous représentez le nombre 12, vous devez tracer 1 ligne parallèle se croisant sur les ensembles de lignes du premier nombre.
-
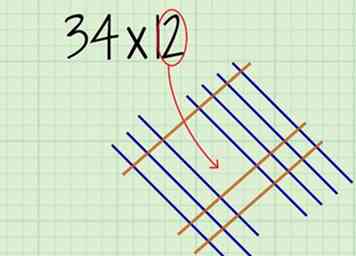 6 Tracez des lignes parallèles pour représenter le lieu de votre deuxième numéro. Le nombre de lignes correspondra au chiffre à la place. Tracez les lignes au-dessous des lignes, de sorte qu'elles traversent toutes les lignes du premier nombre, inclinées dans la direction opposée.
6 Tracez des lignes parallèles pour représenter le lieu de votre deuxième numéro. Le nombre de lignes correspondra au chiffre à la place. Tracez les lignes au-dessous des lignes, de sorte qu'elles traversent toutes les lignes du premier nombre, inclinées dans la direction opposée. - Laissez un espace entre les lignes et les lignes de dizaines, pour pouvoir les distinguer.
- Par exemple, si vous représentez 12, vous allez dessiner 2 lignes parallèles sous la 1 ligne que vous avez dessinée pour la place des dizaines.
-
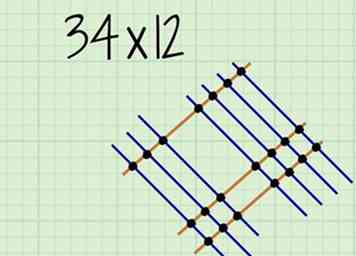 7 Dessinez des points sur chaque point d'intersection des lignes. Dans la méthode de multiplication de ligne, vous allez additionner ces lignes au lieu de les multiplier.
7 Dessinez des points sur chaque point d'intersection des lignes. Dans la méthode de multiplication de ligne, vous allez additionner ces lignes au lieu de les multiplier.
Deuxième partie de deux:
Résoudre le problème
-
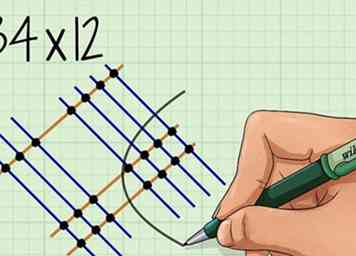 1 Encerclez l'ensemble des points représentant la place de chacun. Ce sont les points formés à l'intersection où se croisent les lignes de chaque nombre.
1 Encerclez l'ensemble des points représentant la place de chacun. Ce sont les points formés à l'intersection où se croisent les lignes de chaque nombre. - Pensez: «Une fois, une est égale à une.»
- Par exemple, pour , vous encercler les points formés lorsque les 4 lignes se croisent avec les 2 lignes, qui sont dans l’ensemble du côté droit du diagramme.
-
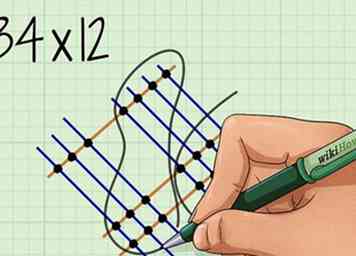 2 Encerclez les deux séries de points représentant la place des dizaines. Ce sont les points formés lorsque le chiffre de l'un des nombres croise le chiffre des dizaines de l'autre nombre.
2 Encerclez les deux séries de points représentant la place des dizaines. Ce sont les points formés lorsque le chiffre de l'un des nombres croise le chiffre des dizaines de l'autre nombre. - Pensez: «Une fois sur dix est égal à dix.»
- Par exemple, pour , vous encercler les points formés lorsque la ligne 1 croise les 4 lignes, et où les 2 lignes se croisent avec les 3 lignes, qui sont au milieu du diagramme.
-
 3 Encerclez l'ensemble des points représentant la place des centaines. Ce sont les points formés à l'intersection où les lignes de dizaines pour chaque nombre se croisent.
3 Encerclez l'ensemble des points représentant la place des centaines. Ce sont les points formés à l'intersection où les lignes de dizaines pour chaque nombre se croisent. - Pensez: «Une dizaine de fois sur dix équivaut à cent.»
- Par exemple, pour , vous encercler les points formés où les 3 lignes se croisent avec la 1 ligne, qui est sur le côté gauche du diagramme.
-
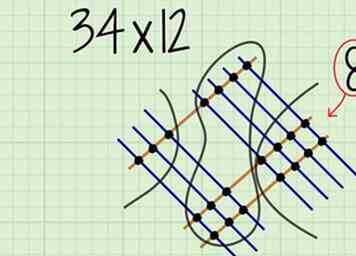 4 Ajoutez les points à la place. Ce sont les points que vous avez encerclés sur le côté droit du diagramme. Ce numéro sera dans le lieu de votre réponse.
4 Ajoutez les points à la place. Ce sont les points que vous avez encerclés sur le côté droit du diagramme. Ce numéro sera dans le lieu de votre réponse. - Pour , vous devriez compter 8 points. Alors sera le chiffre à la place de votre réponse finale.
-
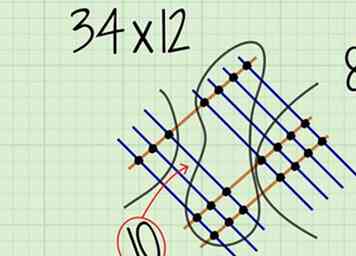 5 Additionnez les points à la place des dizaines. Ce sont les deux jeux de points au milieu du diagramme. Ce numéro sera à la dizaine de votre réponse.
5 Additionnez les points à la place des dizaines. Ce sont les deux jeux de points au milieu du diagramme. Ce numéro sera à la dizaine de votre réponse. - Pour , vous devriez compter 10 points.
- Tout comme chaque fois que vous ajoutez ou multipliez, une fois qu'un chiffre de n'importe quelle valeur atteint 10, vous devez le porter.[4] Donc, si vous comptez 10 pour la place des dizaines, vous placeriez un dans la place des dizaines, et porter le 1 à la place des centaines.
-
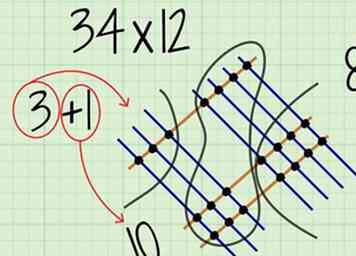 6 Additionnez les points à la place des centaines. Ce sont les points que vous avez encerclés sur le côté gauche du diagramme. Ce nombre sera des centaines de lieu de votre réponse.
6 Additionnez les points à la place des centaines. Ce sont les points que vous avez encerclés sur le côté gauche du diagramme. Ce nombre sera des centaines de lieu de votre réponse. - Pour , vous devriez compter 3 points.
- N'oubliez pas d'ajouter tout montant que vous avez reporté. Pour , vous avez reporté un 1 de la place des dizaines, donc calculer . Alors sera le chiffre à la place des centaines de votre réponse finale.
-
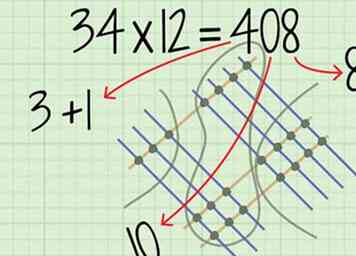 7 Déterminez votre réponse finale. Rassemblez tous les chiffres trouvés pour chaque valeur de lieu.
7 Déterminez votre réponse finale. Rassemblez tous les chiffres trouvés pour chaque valeur de lieu. - Par exemple, pour , vous déterminez un va à la place, un va à la place des dizaines, et un va à la place des centaines. Donc, votre réponse finale est .
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Déterminez les valeurs de position de votre premier numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit.
1 Déterminez les valeurs de position de votre premier numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit.  2 Tracez des lignes parallèles pour représenter la dizaine de votre premier numéro. Le nombre de lignes que vous dessinez correspondra au chiffre à la place des dizaines.
2 Tracez des lignes parallèles pour représenter la dizaine de votre premier numéro. Le nombre de lignes que vous dessinez correspondra au chiffre à la place des dizaines.  3 Tracez des lignes parallèles pour représenter le lieu de votre premier numéro. Le nombre de lignes correspondra au chiffre à la place. Dessinez ces lignes au-dessus et à droite des lignes de dizaines.
3 Tracez des lignes parallèles pour représenter le lieu de votre premier numéro. Le nombre de lignes correspondra au chiffre à la place. Dessinez ces lignes au-dessus et à droite des lignes de dizaines.  4 Déterminez les valeurs de position de votre deuxième numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit.
4 Déterminez les valeurs de position de votre deuxième numéro. Vous devez savoir combien de places sont dans votre numéro et quel chiffre est dans chaque endroit.  5 Tracez des lignes parallèles pour représenter la dizaine de votre deuxième nombre. Le nombre de lignes correspondra au chiffre à la place des dizaines. Tracez les lignes près du haut du diagramme. Ils devraient croiser toutes les lignes du premier nombre, en s'inclinant dans la direction opposée.
5 Tracez des lignes parallèles pour représenter la dizaine de votre deuxième nombre. Le nombre de lignes correspondra au chiffre à la place des dizaines. Tracez les lignes près du haut du diagramme. Ils devraient croiser toutes les lignes du premier nombre, en s'inclinant dans la direction opposée.  6 Tracez des lignes parallèles pour représenter le lieu de votre deuxième numéro. Le nombre de lignes correspondra au chiffre à la place. Tracez les lignes au-dessous des lignes, de sorte qu'elles traversent toutes les lignes du premier nombre, inclinées dans la direction opposée.
6 Tracez des lignes parallèles pour représenter le lieu de votre deuxième numéro. Le nombre de lignes correspondra au chiffre à la place. Tracez les lignes au-dessous des lignes, de sorte qu'elles traversent toutes les lignes du premier nombre, inclinées dans la direction opposée.  7 Dessinez des points sur chaque point d'intersection des lignes. Dans la méthode de multiplication de ligne, vous allez additionner ces lignes au lieu de les multiplier.
7 Dessinez des points sur chaque point d'intersection des lignes. Dans la méthode de multiplication de ligne, vous allez additionner ces lignes au lieu de les multiplier. 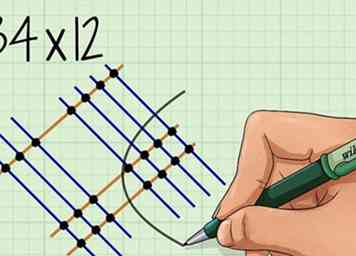 1 Encerclez l'ensemble des points représentant la place de chacun. Ce sont les points formés à l'intersection où se croisent les lignes de chaque nombre.
1 Encerclez l'ensemble des points représentant la place de chacun. Ce sont les points formés à l'intersection où se croisent les lignes de chaque nombre.  2 Encerclez les deux séries de points représentant la place des dizaines. Ce sont les points formés lorsque le chiffre de l'un des nombres croise le chiffre des dizaines de l'autre nombre.
2 Encerclez les deux séries de points représentant la place des dizaines. Ce sont les points formés lorsque le chiffre de l'un des nombres croise le chiffre des dizaines de l'autre nombre.  3 Encerclez l'ensemble des points représentant la place des centaines. Ce sont les points formés à l'intersection où les lignes de dizaines pour chaque nombre se croisent.
3 Encerclez l'ensemble des points représentant la place des centaines. Ce sont les points formés à l'intersection où les lignes de dizaines pour chaque nombre se croisent.  4 Ajoutez les points à la place. Ce sont les points que vous avez encerclés sur le côté droit du diagramme. Ce numéro sera dans le lieu de votre réponse.
4 Ajoutez les points à la place. Ce sont les points que vous avez encerclés sur le côté droit du diagramme. Ce numéro sera dans le lieu de votre réponse.  5 Additionnez les points à la place des dizaines. Ce sont les deux jeux de points au milieu du diagramme. Ce numéro sera à la dizaine de votre réponse.
5 Additionnez les points à la place des dizaines. Ce sont les deux jeux de points au milieu du diagramme. Ce numéro sera à la dizaine de votre réponse.  6 Additionnez les points à la place des centaines. Ce sont les points que vous avez encerclés sur le côté gauche du diagramme. Ce nombre sera des centaines de lieu de votre réponse.
6 Additionnez les points à la place des centaines. Ce sont les points que vous avez encerclés sur le côté gauche du diagramme. Ce nombre sera des centaines de lieu de votre réponse.  7 Déterminez votre réponse finale. Rassemblez tous les chiffres trouvés pour chaque valeur de lieu.
7 Déterminez votre réponse finale. Rassemblez tous les chiffres trouvés pour chaque valeur de lieu.