Êtes-vous gêné par le mal de mémoriser une séquence de nombres aléatoires et intangibles simplement pour effectuer une opération simple comme calculer l'aire d'un cercle? Vous sentez-vous opprimé par le régime qui nous a fait penser à l'inévitable infini des nombres qui constituent la constante irrationnelle π? Aujourd'hui est le jour pour secouer les chaînes! Continuez à lire, et vous découvrirez également comment démêler la vérité cachée que pi réellement est égal à 3.
Pas
-
 1 Sortez une feuille de papier. Si vous voulez vraiment le coller à l'homme, vous voudrez peut-être utiliser autre chose que les feuilles de papier de 8-1 / 2 "x 11".
1 Sortez une feuille de papier. Si vous voulez vraiment le coller à l'homme, vous voudrez peut-être utiliser autre chose que les feuilles de papier de 8-1 / 2 "x 11". -
 2 Configurez votre preuve. En haut du papier, écrivez que a = b.
2 Configurez votre preuve. En haut du papier, écrivez que a = b. - Carré des deux côtés de l'équation.
une2 = b2 - Réécrivez ceci sous une autre forme. Ce sera votre point de départ pour la preuve.
une2 = ab
- Carré des deux côtés de l'équation.
-
 3 Mettre en place une équation secondaire. Multipliez simplement les deux côtés de votre équation la plus récente par 3. Vous devrez incorporer ceci dans votre épreuve plus tard.
3 Mettre en place une équation secondaire. Multipliez simplement les deux côtés de votre équation la plus récente par 3. Vous devrez incorporer ceci dans votre épreuve plus tard. - 3a2 = 3ab
-
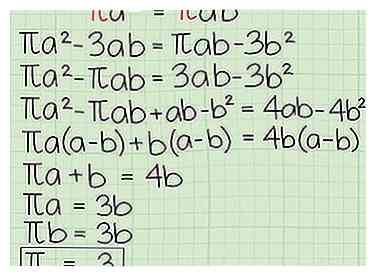 4 Effectuez les opérations suivantes:
4 Effectuez les opérations suivantes: - Multipliez les deux côtés du point de départ de votre épreuve, un2 = ab, par π.
πa2 = πab - Soustraire une (égale) moitié de votre équation secondaire, 3a2 = 3ab, de chaque côté.
πa2 - 3ab = πab - 3b2 - Ajouter 3ab et soustraire πab des deux côtés.
πa2 - πab = 3ab - 3b2 - Ajouter ab et soustraire b2 sur les deux côtés.
πa2 - πab + ab - b2 = 4ab - 4b2 - Comptez les termes courants.
πa (a-b) + b (a-b) = 4b (a-b) - Supprimer les termes communs.
πa + b = 4b - Soustrayez b des deux côtés.
πa = 3b - Remplacez a pour b (puisque a = b).
πb = 3b - Supprimer les termes communs.
π = 3
- Multipliez les deux côtés du point de départ de votre épreuve, un2 = ab, par π.
-
 5 Laissez échapper un soupçon d'incrédulité! Combien d'années de souffrances inutiles avez-vous endurées en mathématiques, en calculant l'aire d'un cercle avec le 3,14 clairement fabriqué, ou pire encore, 3,1416?
5 Laissez échapper un soupçon d'incrédulité! Combien d'années de souffrances inutiles avez-vous endurées en mathématiques, en calculant l'aire d'un cercle avec le 3,14 clairement fabriqué, ou pire encore, 3,1416? -
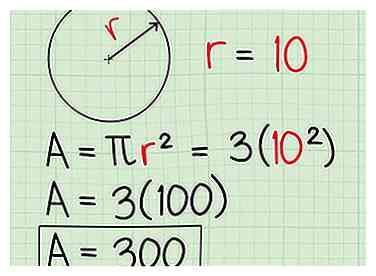 6 Prenez le temps de savourer votre nouvelle liberté en calculant des zones et des volumes avec la nouvelle valeur de π: 3. Maintenant, c'est parfaitement facile: avec un cercle de rayon 10 unités, la zone est de rayon π *2ou 3 * 102 = 300 unités2. Ah, le pouvoir!
6 Prenez le temps de savourer votre nouvelle liberté en calculant des zones et des volumes avec la nouvelle valeur de π: 3. Maintenant, c'est parfaitement facile: avec un cercle de rayon 10 unités, la zone est de rayon π *2ou 3 * 102 = 300 unités2. Ah, le pouvoir! -
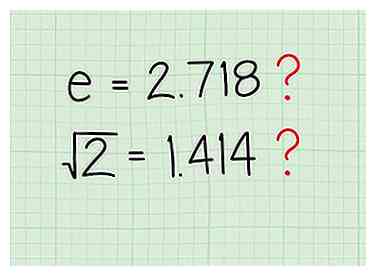 7 Pourquoi s'arrêter à π? Vous avez peut-être été l'un des pauvres élèves asservis qui ont également utilisé 2,718 pour e ou 1,414 pour la racine carrée de 2. Soyez libre de tous!
7 Pourquoi s'arrêter à π? Vous avez peut-être été l'un des pauvres élèves asservis qui ont également utilisé 2,718 pour e ou 1,414 pour la racine carrée de 2. Soyez libre de tous!
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Sortez une feuille de papier. Si vous voulez vraiment le coller à l'homme, vous voudrez peut-être utiliser autre chose que les feuilles de papier de 8-1 / 2 "x 11".
1 Sortez une feuille de papier. Si vous voulez vraiment le coller à l'homme, vous voudrez peut-être utiliser autre chose que les feuilles de papier de 8-1 / 2 "x 11".  2 Configurez votre preuve. En haut du papier, écrivez que a = b.
2 Configurez votre preuve. En haut du papier, écrivez que a = b.  3 Mettre en place une équation secondaire. Multipliez simplement les deux côtés de votre équation la plus récente par 3. Vous devrez incorporer ceci dans votre épreuve plus tard.
3 Mettre en place une équation secondaire. Multipliez simplement les deux côtés de votre équation la plus récente par 3. Vous devrez incorporer ceci dans votre épreuve plus tard. 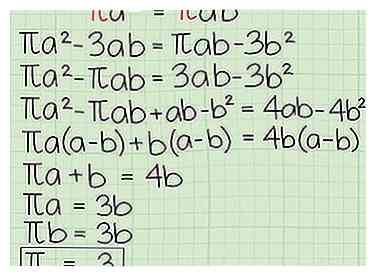 4 Effectuez les opérations suivantes:
4 Effectuez les opérations suivantes:  5 Laissez échapper un soupçon d'incrédulité! Combien d'années de souffrances inutiles avez-vous endurées en mathématiques, en calculant l'aire d'un cercle avec le 3,14 clairement fabriqué, ou pire encore, 3,1416?
5 Laissez échapper un soupçon d'incrédulité! Combien d'années de souffrances inutiles avez-vous endurées en mathématiques, en calculant l'aire d'un cercle avec le 3,14 clairement fabriqué, ou pire encore, 3,1416? 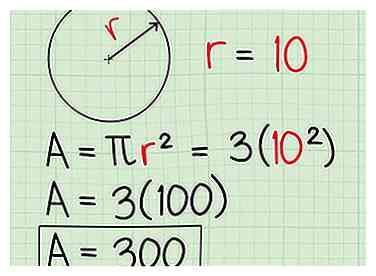 6 Prenez le temps de savourer votre nouvelle liberté en calculant des zones et des volumes avec la nouvelle valeur de π: 3. Maintenant, c'est parfaitement facile: avec un cercle de rayon 10 unités, la zone est de rayon π *2ou 3 * 102 = 300 unités2. Ah, le pouvoir!
6 Prenez le temps de savourer votre nouvelle liberté en calculant des zones et des volumes avec la nouvelle valeur de π: 3. Maintenant, c'est parfaitement facile: avec un cercle de rayon 10 unités, la zone est de rayon π *2ou 3 * 102 = 300 unités2. Ah, le pouvoir! 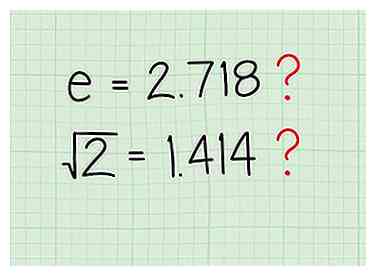 7 Pourquoi s'arrêter à π? Vous avez peut-être été l'un des pauvres élèves asservis qui ont également utilisé 2,718 pour e ou 1,414 pour la racine carrée de 2. Soyez libre de tous!
7 Pourquoi s'arrêter à π? Vous avez peut-être été l'un des pauvres élèves asservis qui ont également utilisé 2,718 pour e ou 1,414 pour la racine carrée de 2. Soyez libre de tous!