En statistique, le mode d'un ensemble de chiffres est le numéro qui apparaît le plus souvent dans l'ensemble. Un ensemble de données ne doit pas nécessairement avoir un seul mode - si deux valeurs ou plus sont "liées" pour être les plus courantes, on peut dire que l'ensemble est bimodal ou multimodal, respectivement - en d'autres termes, toutes les valeurs les plus courantes sont les modes de l'ensemble. Pour un aperçu détaillé du processus de détermination du ou des modes d'un ensemble de données, voir l'étape 1 ci-dessous pour commencer.

Méthode One of Two:
Recherche du mode d'un jeu de données

  1. 1 Écrivez les numéros dans votre jeu de données. Les modes sont généralement issus d'ensembles de points de données statistiques ou de listes de valeurs numériques. Ainsi, pour trouver un mode, vous aurez besoin d'un jeu de données pour le trouver. Il est difficile d'effectuer des calculs de mode mentalement pour tous les jeux de données, sauf le plus petit. Par conséquent, dans la plupart des cas, il est conseillé de commencer par écrire (ou taper) vos données. Si vous travaillez avec du papier et un crayon, il suffira d'écrire simplement les valeurs de votre ensemble de données. Si vous utilisez un ordinateur, vous souhaiterez peut-être utiliser un tableur pour simplifier le processus.
    • Le processus de recherche d'un mode de jeu de données est plus facile à comprendre en suivant un exemple de problème. Dans cette section, utilisons cet ensemble de valeurs pour les besoins de notre exemple: 18, 21, 11, 21, 15, 19, 17, 21, 17. Dans les prochaines étapes, nous trouverons le mode de cet ensemble.
  2. 2 Commandez les numéros du plus petit au plus grand. Ensuite, il est souvent judicieux de trier les valeurs de votre jeu de données pour qu'elles soient en ordre croissant. Bien que cela ne soit pas strictement requis, le processus de recherche du mode est facilité car il regroupe des valeurs identiques les unes à côté des autres. Pour les grands ensembles de données, cela peut être pratiquement une nécessité, car il est difficile de faire le tri parmi de longues listes de valeurs et de déterminer combien de fois chaque numéro apparaît dans la liste, ce qui peut entraîner des erreurs.
    • Si vous travaillez avec du papier et un crayon, la réécriture peut vous faire gagner du temps à long terme. Analysez le jeu de nombres pour le nombre le plus bas et, lorsque vous le trouvez, recoupez-le dans le premier jeu de données et réécrivez-le dans votre nouveau jeu de données. Répétez l'opération pour le deuxième nombre le plus bas, troisième plus bas, etc., en vous assurant d'écrire chaque nombre autant de fois qu'il se produit dans le jeu de données d'origine.
    • Avec un ordinateur, vos options sont plus étendues - par exemple, la plupart des tableurs auront la possibilité de réorganiser des listes de valeurs du plus petit au plus grand en quelques clics seulement.
    • Dans notre exemple, après la réorganisation, la nouvelle liste de valeurs doit se lire comme suit: 11, 15, 17, 17, 18, 19, 21, 21, 21.
  3. 3 Comptez le nombre de fois que chaque nombre est répété. Ensuite, compter le nombre de fois que chaque numéro de l'ensemble apparaît. Recherchez la valeur la plus courante dans l'ensemble de données. Pour des ensembles de données relativement petits avec des points disposés dans l'ordre croissant, il s'agit généralement de trouver le plus grand "cluster" de valeurs identiques et de compter le nombre d'occurrences.
    • Si vous travaillez avec un crayon et du papier, pour garder une trace de vos comptes, essayez d'écrire le nombre de fois où chaque valeur apparaît au-dessus de chaque groupe de nombres identiques. Si vous utilisez un tableur sur un ordinateur, vous pouvez faire la même chose en écrivant vos totaux dans des cellules adjacentes ou en utilisant l'une des options du programme pour comptabiliser les points de données.
    • Dans notre exemple (11, 15, 17, 17, 18, 19, 21, 21, 21), 11 survient une fois, 15 une fois, 17 deux fois, 18 une fois, 19 une fois et 21 se produit trois fois. 21 est la valeur la plus courante dans cet ensemble de données.
  4. 4 Identifiez la valeur (ou les valeurs) la plus fréquente. Lorsque vous savez combien de fois chaque valeur apparaît dans votre ensemble de données, recherchez la valeur qui se produit le plus grand nombre de fois. Ceci est le mode de votre ensemble de données. Notez que il peut y avoir plus d'un mode dans un ensemble de données. Si les deux valeurs sont liées pour être les valeurs les plus communes de l'ensemble, on peut dire que l'ensemble de données est bimodal, alors que si trois valeurs sont liées, l’ensemble est trimodal, etc.
    • Dans notre exemple, (11, 15, 17, 17, 18, 19, 21, 21, 21), car 21 se produit plus de fois que toute autre valeur, 21 est le mode.
    • Si une valeur autre que 21 avait aussi survenu trois fois (par exemple, s'il y en avait un autre 17 dans l'ensemble de données), 21 et cet autre tous les deux être le mode.
  5. 5 Ne confondez pas le mode d'un ensemble de données avec sa moyenne ou sa médiane. Trois concepts statistiques souvent discutés ensemble sont les moyens, les médianes et les modes. Parce que ces concepts ont tous des noms similaires et que, pour un seul ensemble de données, une seule valeur peut parfois être plus d'un de ces choses, il est facile de les confondre. Cependant, que le mode de jeu de données soit également médian ou moyen, il est important de comprendre que ces trois concepts sont totalement indépendants les uns des autres. Voir ci-dessous:
    • Un ensemble de données signifier est sa moyenne. Pour trouver le moyen, additionnez toutes les valeurs du jeu de données, puis divisez-le par le nombre de valeurs du jeu. Par exemple, pour notre ensemble de données d'exemple (11, 15, 17, 17, 18, 19, 21, 21, 21), la moyenne serait de 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160/9 = 17.78. Notez que nous avons divisé la somme des valeurs par 9 car il y a un total de 9 valeurs dans le jeu de données.
    • Un ensemble de données médian est le "nombre intermédiaire" séparant les valeurs inférieures et supérieures d'un ensemble de données en deux moitiés égales. Par exemple, dans notre exemple de jeu de données (11, 15, 17, 17, 18, 19, 21, 21, 21) 18 est la médiane, car il s'agit du nombre moyen - il y a exactement quatre chiffres plus haut et quatre chiffres plus bas.Notez que s'il y a un nombre pair de valeurs dans l'ensemble de données, il n'y a pas de médiane unique. Dans ces cas, la médiane est généralement considérée comme la moyenne des deux nombres intermédiaires.

Méthode deux sur deux:
Trouver le mode dans des cas spéciaux

  1. 1 Reconnaître qu’il n’existe aucun mode pour les ensembles de données dans lesquels chaque valeur est identique. Si les valeurs d'un ensemble donné se produisent toutes le même nombre de fois, le jeu de données n'a pas de mode car aucun nombre n'est plus commun que tout autre. Par exemple, les ensembles de données dans lesquels chaque valeur apparaît une fois ne comportent aucun mode. Il en va de même pour les jeux de données dans lesquels chaque valeur apparaît deux fois, trois fois, etc.
    • Si nous modifions notre ensemble de données exemple sur 11, 15, 17, 18, 19, 21 afin que chaque valeur ne se produise qu’une seule fois, le jeu de données a maintenant pas de mode. La même chose est vraie si nous modifions le jeu de données pour que chaque valeur apparaisse deux fois: 11, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21.
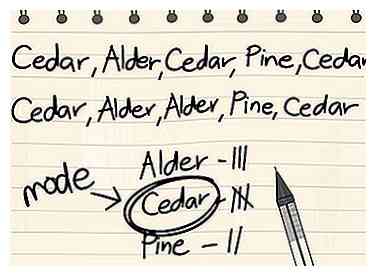  2. 2 Reconnaître que les modes pour les ensembles de données non numériques peuvent être trouvés de la même manière que pour les ensembles de données numériques. Généralement, la plupart des ensembles de données sont quantitatif - ils traitent des données sous forme de nombres. Cependant, certains ensembles de données traitent de données qui ne sont pas exprimées sous forme de nombres. Dans ces cas, le «mode» peut être considéré comme la valeur unique qui se produit le plus dans le jeu de données, tout comme pour les ensembles de données numériques.[1] Dans ces cas, il peut être possible de trouver le mode tout en étant impossible de trouver une médiane ou une moyenne significative pour l'ensemble de données.
    • Par exemple, supposons qu'une enquête biologique détermine les espèces de chaque arbre dans une petite partie locale. L'ensemble de données pour les types d'arbres du parc est Cedar, Aulne, Cèdre, Pin, Cèdre, Cèdre, Aulne, Aulne, Pin, Cèdre. Ce type de jeu de données est appelé nominal ensemble de données car les points de données ne se distinguent que par leurs noms. Dans ce cas, le mode du jeu de données est Cèdre car il se produit le plus souvent (cinq fois contre trois pour l’alder et deux pour le pin).
    • Notez que, pour l'exemple de données ci-dessus, il est impossible de calculer une moyenne ou une médiane car les points de données n'ont aucune valeur numérique.
  3. 3 Reconnaître que pour les distributions symétriques unimodales, le mode, la moyenne et la médiane coïncident. Comme indiqué ci-dessus, il est possible que le mode, la médiane et / ou la moyenne se chevauchent dans certains cas. Dans des cas spéciaux, sélectionnez les cas où la fonction de densité de l'ensemble de données forme une courbe parfaitement symétrique avec un mode (par exemple, la courbe gaussienne ou "en forme de cloche"), le mode, la moyenne et la médiane auront tous la même valeur. Comme une fonction de distribution représente l'occurrence relative des points de données, le mode se situera naturellement au milieu d'une courbe de distribution symétrique, car il s'agit du point le plus élevé du graphique et correspond à la valeur la plus commune. Comme l'ensemble de données est symétrique, ce point sur le graphique correspondra à la médiane - la valeur intermédiaire de l'ensemble de données - et à la moyenne - la moyenne de l'ensemble de données.
    • Par exemple, considérons l'ensemble de données 1, 2, 2, 3, 3, 3, 4, 4, 5. Si nous devions représenter graphiquement la distribution de cet ensemble de données, nous aurions une courbe symétrique qui atteindrait une hauteur de 3 à x = 3 et diminuerait à une hauteur de 1 à x = 1 et x = 5. Parce que 3 est la valeur la plus commune, c'est le mode. Parce que le central 3 dans le jeu de données a 4 valeurs de chaque côté, 3 est aussi la médiane. Enfin, la moyenne de l’ensemble de données s’établit à 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3, ce qui signifie que 3 est aussi la moyenne.
    • L'exception à cette règle concerne les ensembles de données symétriques avec plus d'un mode - dans ce cas, comme il ne peut y avoir qu'une seule médiane et moyenne pour l'ensemble de données, les deux modes ne coïncideront pas avec ces autres points.