Les factoriels sont couramment utilisés lors du calcul des probabilités et des permutations, ou des ordres d'événements possibles.[1] Une factorielle est désignée par un signifier, et cela signifie multiplier tous les nombres qui descendent du nombre factoriel. Une fois que vous avez compris ce qu'est une factorielle, il est simple à calculer, notamment à l'aide d'une calculatrice scientifique.
Méthode One of Three:
Calculer un facteur
-
 1 Déterminez le nombre pour lequel vous calculez la factorielle. Une factorielle est désignée par un entier positif et un point d'exclamation.
1 Déterminez le nombre pour lequel vous calculez la factorielle. Une factorielle est désignée par un entier positif et un point d'exclamation. - Par exemple, si vous devez calculer la factorielle pour 5, vous verrez .
-
 2 Écrivez la séquence de nombres à multiplier. Une factorielle multiplie simplement les nombres naturels qui descendent séquentiellement du nombre factoriel, jusqu'à 1.[2] Parlant de manière formelle, , où est égal à tout nombre entier positif.[3]
2 Écrivez la séquence de nombres à multiplier. Une factorielle multiplie simplement les nombres naturels qui descendent séquentiellement du nombre factoriel, jusqu'à 1.[2] Parlant de manière formelle, , où est égal à tout nombre entier positif.[3] - Par exemple, si vous calculez , vous calculeriez ou, plus simplement noté: .
-
 3 Multipliez les nombres ensemble. Vous pouvez calculer une factorielle rapidement en utilisant une calculatrice scientifique, qui devrait avoir un signe. Si vous calculez à la main, pour plus de facilité, commencez par rechercher des paires de facteurs qui se multiplient pour atteindre 10.[4] Bien sûr, vous pouvez également ignorer le 1, car tout nombre multiplié par 1 est égal à ce nombre.
3 Multipliez les nombres ensemble. Vous pouvez calculer une factorielle rapidement en utilisant une calculatrice scientifique, qui devrait avoir un signe. Si vous calculez à la main, pour plus de facilité, commencez par rechercher des paires de facteurs qui se multiplient pour atteindre 10.[4] Bien sûr, vous pouvez également ignorer le 1, car tout nombre multiplié par 1 est égal à ce nombre. - Par exemple, si l'informatique , ignorez le 1 et calculez d'abord . Maintenant tout ce qui vous reste est . Depuis , Tu le sais .
Méthode deux sur trois:
Simplifier un factoriel
-
 1 Déterminez l'expression que vous simplifiez. Souvent, cela sera indiqué comme une fraction.
1 Déterminez l'expression que vous simplifiez. Souvent, cela sera indiqué comme une fraction. - Par exemple, vous pourriez avoir besoin de simplifier .
-
 2 Notez les facteurs de chaque factorielle. Depuis la factorielle est un facteur de plus grande taille, pour simplifier, vous devez rechercher des facteurs que vous pouvez annuler.[5] C'est facile à faire si vous écrivez chaque terme.[6]
2 Notez les facteurs de chaque factorielle. Depuis la factorielle est un facteur de plus grande taille, pour simplifier, vous devez rechercher des facteurs que vous pouvez annuler.[5] C'est facile à faire si vous écrivez chaque terme.[6] - Par exemple, si simplifier , réécrire comme
-
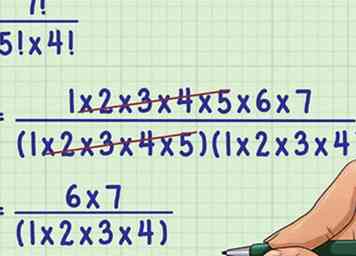 3 Annulez tous les termes communs au numérateur et au dénominateur.[7] Cela simplifiera les surplus de nombres que vous devez multiplier.
3 Annulez tous les termes communs au numérateur et au dénominateur.[7] Cela simplifiera les surplus de nombres que vous devez multiplier. - Par exemple, depuis est un facteur de , vous pouvez annuler du numérateur et du dénominateur:
- Par exemple, depuis est un facteur de , vous pouvez annuler du numérateur et du dénominateur:
-
 4 Complétez les calculs. Simplifier si possible. Cela vous donnera la dernière expression simplifiée.
4 Complétez les calculs. Simplifier si possible. Cela vous donnera la dernière expression simplifiée. - Par exemple:
Alors, est simplifié .
- Par exemple:
Méthode trois sur trois:
Faire des exemples de problèmes factoriels
-
 1 Évaluez l'expression 8!.
1 Évaluez l'expression 8!. - Si vous utilisez une calculatrice scientifique, appuyez sur la touche clé, suivi du clé.
- Si vous résolvez à la main, écrivez les facteurs à multiplier:
- Ne tenez pas compte du 1:
- Extraire :
- Groupez d'abord tout autre nombre facilement multiplié, puis multipliez tous les produits ensemble:
Alors, .
-
 2 Simplifiez l'expression: .
2 Simplifiez l'expression: . - Notez les facteurs de chaque factorielle:
- Annuler les termes communs au numérateur et au dénominateur:
- Complétez les calculs:
Donc, l'expression simplifie à .
- Notez les facteurs de chaque factorielle:
-
 3 Essayez le problème suivant. Vous avez 6 peintures que vous voudriez afficher dans une rangée sur votre mur. Combien de façons différentes pouvez-vous commander les peintures?
3 Essayez le problème suivant. Vous avez 6 peintures que vous voudriez afficher dans une rangée sur votre mur. Combien de façons différentes pouvez-vous commander les peintures? - Puisque vous recherchez différentes manières de commander des objets, vous pouvez simplement résoudre le problème en trouvant la factorielle correspondant au nombre d'objets.
- Le nombre d'arrangements possibles pour 6 peintures accrochées dans une rangée peut être résolu en trouvant .
- Si vous utilisez une calculatrice scientifique, appuyez sur la touche clé, suivi du clé.
- Si vous résolvez à la main, écrivez les facteurs à multiplier:
- Ne tenez pas compte du 1:
- Extraire :
- Groupez d'abord tout autre nombre facilement multiplié, puis multipliez tous les produits ensemble:
Ainsi, 6 tableaux accrochés en rang peuvent être commandés de 720 manières différentes.
-
 4 Essayez le problème suivant. Vous avez 6 peintures. Vous souhaitez afficher 3 d'entre eux sur votre mur. Combien de façons différentes pouvez-vous commander 3 des peintures?
4 Essayez le problème suivant. Vous avez 6 peintures. Vous souhaitez afficher 3 d'entre eux sur votre mur. Combien de façons différentes pouvez-vous commander 3 des peintures? - Puisque vous avez 6 peintures différentes, mais que vous n'en choisissez que 3, il vous suffit de multiplier les 3 premiers chiffres de la séquence pour la factorielle de 6. Vous pouvez également utiliser la formule , où est égal au nombre d'objets parmi lesquels vous choisissez, et est égal au nombre d'objets que vous utilisez. Cette formule ne fonctionne que si vous n'avez pas de répétitions (un objet ne peut pas être choisi plus d'une fois), et l'ordre compte (c'est-à-dire que vous voulez trouver combien de façons différentes les choses peuvent être commandées).[8]
- Le nombre d'arrangements possibles pour 3 peintures choisies parmi 6 et accrochées dans une rangée peut être résolu en trouvant .
- Soustraire les nombres au dénominateur:
- Écrivez les facteurs de chaque factorielle:
- Annuler les termes communs au numérateur et au dénominateur:
- Complétez les calculs:
Ainsi, 3 peintures choisies parmi 6 peuvent être commandées de 120 manières différentes si elles sont alignées.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Déterminez le nombre pour lequel vous calculez la factorielle. Une factorielle est désignée par un entier positif et un point d'exclamation.
1 Déterminez le nombre pour lequel vous calculez la factorielle. Une factorielle est désignée par un entier positif et un point d'exclamation.  2 Écrivez la séquence de nombres à multiplier. Une factorielle multiplie simplement les nombres naturels qui descendent séquentiellement du nombre factoriel, jusqu'à 1.[2] Parlant de manière formelle,
2 Écrivez la séquence de nombres à multiplier. Une factorielle multiplie simplement les nombres naturels qui descendent séquentiellement du nombre factoriel, jusqu'à 1.[2] Parlant de manière formelle,  3 Multipliez les nombres ensemble. Vous pouvez calculer une factorielle rapidement en utilisant une calculatrice scientifique, qui devrait avoir un
3 Multipliez les nombres ensemble. Vous pouvez calculer une factorielle rapidement en utilisant une calculatrice scientifique, qui devrait avoir un  1 Déterminez l'expression que vous simplifiez. Souvent, cela sera indiqué comme une fraction.
1 Déterminez l'expression que vous simplifiez. Souvent, cela sera indiqué comme une fraction.  2 Notez les facteurs de chaque factorielle. Depuis la factorielle
2 Notez les facteurs de chaque factorielle. Depuis la factorielle 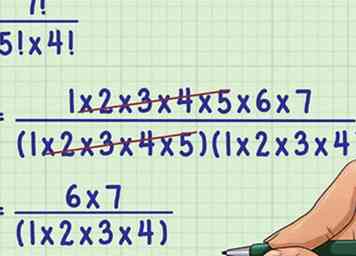 3 Annulez tous les termes communs au numérateur et au dénominateur.[7] Cela simplifiera les surplus de nombres que vous devez multiplier.
3 Annulez tous les termes communs au numérateur et au dénominateur.[7] Cela simplifiera les surplus de nombres que vous devez multiplier.  4 Complétez les calculs. Simplifier si possible. Cela vous donnera la dernière expression simplifiée.
4 Complétez les calculs. Simplifier si possible. Cela vous donnera la dernière expression simplifiée.  1 Évaluez l'expression 8!.
1 Évaluez l'expression 8!.  2 Simplifiez l'expression:
2 Simplifiez l'expression:  3 Essayez le problème suivant. Vous avez 6 peintures que vous voudriez afficher dans une rangée sur votre mur. Combien de façons différentes pouvez-vous commander les peintures?
3 Essayez le problème suivant. Vous avez 6 peintures que vous voudriez afficher dans une rangée sur votre mur. Combien de façons différentes pouvez-vous commander les peintures?  4 Essayez le problème suivant. Vous avez 6 peintures. Vous souhaitez afficher 3 d'entre eux sur votre mur. Combien de façons différentes pouvez-vous commander 3 des peintures?
4 Essayez le problème suivant. Vous avez 6 peintures. Vous souhaitez afficher 3 d'entre eux sur votre mur. Combien de façons différentes pouvez-vous commander 3 des peintures?