L'IQR est la "plage interquartile" d'un ensemble de données. Il est utilisé dans l'analyse statistique pour aider à tirer des conclusions sur un ensemble de chiffres. L'IQR est souvent préféré à la gamme car il exclut la plupart des valeurs aberrantes. Lisez la suite pour apprendre à trouver l'IQR!
Méthode One of Three:
Comprendre l'IQR
-
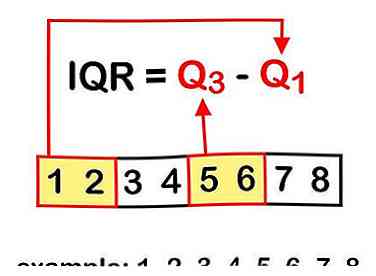 1 Savoir comment utiliser l'IQR. Il s’agit essentiellement d’un moyen de comprendre la propagation ou la «dispersion» d’un ensemble de nombres.[1] L'intervalle interquartile est défini comme la différence entre le quartile supérieur (le plus élevé de 25%) et le quartile inférieur (le plus faible de 25%) d'un ensemble de données. Le quartile inférieur est généralement écrit Q1 et le quartile supérieur Q3 - ce qui rendrait techniquement le point à mi-chemin de l'ensemble de données Q2 et le point Q4 le plus élevé.[2]
1 Savoir comment utiliser l'IQR. Il s’agit essentiellement d’un moyen de comprendre la propagation ou la «dispersion» d’un ensemble de nombres.[1] L'intervalle interquartile est défini comme la différence entre le quartile supérieur (le plus élevé de 25%) et le quartile inférieur (le plus faible de 25%) d'un ensemble de données. Le quartile inférieur est généralement écrit Q1 et le quartile supérieur Q3 - ce qui rendrait techniquement le point à mi-chemin de l'ensemble de données Q2 et le point Q4 le plus élevé.[2] -
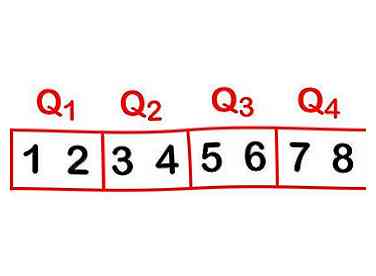 2 Comprendre les quartiles. Pour visualiser un quartile, découpez une liste de nombres en quatre parties égales. Chacune de ces parties est un "quartile".[3] Considérons l'ensemble: 1, 2, 3, 4, 5, 6, 7, 8.
2 Comprendre les quartiles. Pour visualiser un quartile, découpez une liste de nombres en quatre parties égales. Chacune de ces parties est un "quartile".[3] Considérons l'ensemble: 1, 2, 3, 4, 5, 6, 7, 8. - 1 et 2 sont le premier quartile, ou Q1
- 3 et 4 sont le deuxième quartile, ou Q2
- 5 et 6 sont le troisième quartile, ou Q3
- 7 et 8 sont le quatrième quartile, ou Q4
-
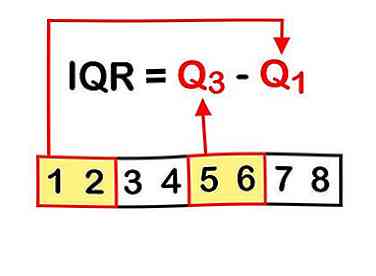 3 Apprenez la formule. Pour trouver la différence entre le quartile supérieur et inférieur, vous devez soustraire le 25e centile du 75e centile. La formule est écrite comme suit: Q3 - Q1 = IQR.[4]
3 Apprenez la formule. Pour trouver la différence entre le quartile supérieur et inférieur, vous devez soustraire le 25e centile du 75e centile. La formule est écrite comme suit: Q3 - Q1 = IQR.[4]
Méthode deux sur trois:
Organisation du jeu de données
-
 1 Rassemblez vos données. Si vous apprenez cela pour un cours et que vous passez un test, vous pourriez recevoir un ensemble de chiffres prêts à l'emploi, par ex. 1, 4, 5, 7, 10. Ceci est votre ensemble de données - les numéros avec lesquels vous allez travailler. Toutefois, vous devrez peut-être organiser vous-même les numéros à partir d'un problème de table ou de mot. Assurez-vous que chaque numéro se rapporte au même genre de chose: par exemple, le nombre d'œufs dans chaque nid d'une population d'oiseaux donnée, ou le nombre de places de stationnement attachées à chaque maison sur un bloc donné.[5]
1 Rassemblez vos données. Si vous apprenez cela pour un cours et que vous passez un test, vous pourriez recevoir un ensemble de chiffres prêts à l'emploi, par ex. 1, 4, 5, 7, 10. Ceci est votre ensemble de données - les numéros avec lesquels vous allez travailler. Toutefois, vous devrez peut-être organiser vous-même les numéros à partir d'un problème de table ou de mot. Assurez-vous que chaque numéro se rapporte au même genre de chose: par exemple, le nombre d'œufs dans chaque nid d'une population d'oiseaux donnée, ou le nombre de places de stationnement attachées à chaque maison sur un bloc donné.[5] -
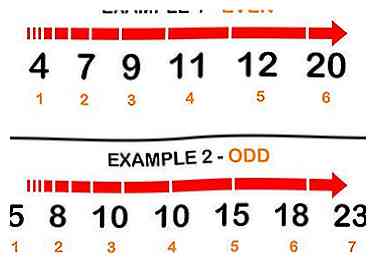 2 Organisez vos données en ordre croissant. En d'autres termes: arrangez les nombres du plus bas au plus haut. Répondez aux exemples suivants.
2 Organisez vos données en ordre croissant. En d'autres termes: arrangez les nombres du plus bas au plus haut. Répondez aux exemples suivants. - Nombre pair d'exemple de données (Set A): 4 7 9 11 12 20
- Nombre impair d’exemple de données (Set B): 5 8 10 10 15 18 23
-
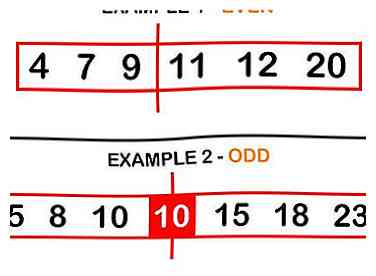 3 Diviser les données en deux. Pour ce faire, recherchez le point milieu de vos données: le ou les nombres au centre de l’ensemble. Si vous avez un nombre impair de nombres, choisissez le nombre exact exact. Si vous avez un nombre pair de nombres, le point milieu reposera entre les deux nombres intermédiaires.
3 Diviser les données en deux. Pour ce faire, recherchez le point milieu de vos données: le ou les nombres au centre de l’ensemble. Si vous avez un nombre impair de nombres, choisissez le nombre exact exact. Si vous avez un nombre pair de nombres, le point milieu reposera entre les deux nombres intermédiaires. - Même exemple (Set A), dans lequel le point médian se situe entre 9 et 11: 4 7 9 | 11 12 20
- Exemple impair (Set B), dans lequel (10) est le milieu: 5 8 10 (10) 15 18 23
Méthode trois sur trois:
Calcul du IQR
-
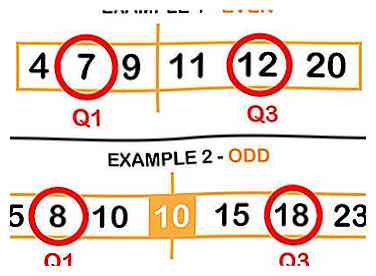 1 Trouvez la médiane de la moitié inférieure et supérieure de vos données. La médiane est le "milieu" ou le nombre qui est à mi-chemin dans un ensemble.[6] Dans ce cas, vous ne recherchez pas le milieu de l'ensemble, mais plutôt les points médians relatifs des sous-ensembles supérieur et inférieur. Si vous avez un nombre impair de données, n'incluez pas le chiffre du milieu - dans Set B, par exemple, vous ne figureriez pas dans l'un des 10.[7]
1 Trouvez la médiane de la moitié inférieure et supérieure de vos données. La médiane est le "milieu" ou le nombre qui est à mi-chemin dans un ensemble.[6] Dans ce cas, vous ne recherchez pas le milieu de l'ensemble, mais plutôt les points médians relatifs des sous-ensembles supérieur et inférieur. Si vous avez un nombre impair de données, n'incluez pas le chiffre du milieu - dans Set B, par exemple, vous ne figureriez pas dans l'un des 10.[7] - Même exemple (Set A):
- Médiane de la moitié inférieure = 7 (Q1)
- Médiane de la moitié supérieure = 12 (Q3)
- Exemple impair (Set B):
- Médiane de la moitié inférieure = 8 (Q1)
- Médiane de la moitié supérieure = 18 (Q3)
- Même exemple (Set A):
-
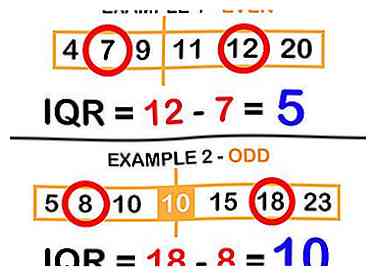 2 Soustraire Q3 - Q1 pour déterminer l'IQR. Vous savez maintenant combien de nombres se situent entre le 25e centile et le 75e centile. Vous pouvez l'utiliser pour comprendre la diffusion des données. Par exemple, si un test est noté sur 100 et que le QI des scores est de 5, vous pouvez supposer que la plupart des personnes qui le prennent ont une compréhension similaire du fait que la fourchette haute n'est pas très grande. Si le IQR des résultats des tests est de 30, cependant, vous pourriez commencer à vous demander pourquoi certaines personnes ont obtenu des résultats aussi élevés et d'autres si bas.
2 Soustraire Q3 - Q1 pour déterminer l'IQR. Vous savez maintenant combien de nombres se situent entre le 25e centile et le 75e centile. Vous pouvez l'utiliser pour comprendre la diffusion des données. Par exemple, si un test est noté sur 100 et que le QI des scores est de 5, vous pouvez supposer que la plupart des personnes qui le prennent ont une compréhension similaire du fait que la fourchette haute n'est pas très grande. Si le IQR des résultats des tests est de 30, cependant, vous pourriez commencer à vous demander pourquoi certaines personnes ont obtenu des résultats aussi élevés et d'autres si bas. - Même exemple (Set A): 12 - 7 = 5
- Exemple impair (Set B): 18 - 8 = 10
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Savoir comment utiliser l'IQR. Il s’agit essentiellement d’un moyen de comprendre la propagation ou la «dispersion» d’un ensemble de nombres.[1] L'intervalle interquartile est défini comme la différence entre le quartile supérieur (le plus élevé de 25%) et le quartile inférieur (le plus faible de 25%) d'un ensemble de données. Le quartile inférieur est généralement écrit Q1 et le quartile supérieur Q3 - ce qui rendrait techniquement le point à mi-chemin de l'ensemble de données Q2 et le point Q4 le plus élevé.[2]
1 Savoir comment utiliser l'IQR. Il s’agit essentiellement d’un moyen de comprendre la propagation ou la «dispersion» d’un ensemble de nombres.[1] L'intervalle interquartile est défini comme la différence entre le quartile supérieur (le plus élevé de 25%) et le quartile inférieur (le plus faible de 25%) d'un ensemble de données. Le quartile inférieur est généralement écrit Q1 et le quartile supérieur Q3 - ce qui rendrait techniquement le point à mi-chemin de l'ensemble de données Q2 et le point Q4 le plus élevé.[2] 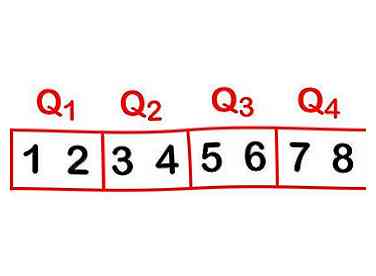 2 Comprendre les quartiles. Pour visualiser un quartile, découpez une liste de nombres en quatre parties égales. Chacune de ces parties est un "quartile".[3] Considérons l'ensemble: 1, 2, 3, 4, 5, 6, 7, 8.
2 Comprendre les quartiles. Pour visualiser un quartile, découpez une liste de nombres en quatre parties égales. Chacune de ces parties est un "quartile".[3] Considérons l'ensemble: 1, 2, 3, 4, 5, 6, 7, 8.  3 Apprenez la formule. Pour trouver la différence entre le quartile supérieur et inférieur, vous devez soustraire le 25e centile du 75e centile. La formule est écrite comme suit: Q3 - Q1 = IQR.[4]
3 Apprenez la formule. Pour trouver la différence entre le quartile supérieur et inférieur, vous devez soustraire le 25e centile du 75e centile. La formule est écrite comme suit: Q3 - Q1 = IQR.[4]  1 Rassemblez vos données. Si vous apprenez cela pour un cours et que vous passez un test, vous pourriez recevoir un ensemble de chiffres prêts à l'emploi, par ex. 1, 4, 5, 7, 10. Ceci est votre ensemble de données - les numéros avec lesquels vous allez travailler. Toutefois, vous devrez peut-être organiser vous-même les numéros à partir d'un problème de table ou de mot. Assurez-vous que chaque numéro se rapporte au même genre de chose: par exemple, le nombre d'œufs dans chaque nid d'une population d'oiseaux donnée, ou le nombre de places de stationnement attachées à chaque maison sur un bloc donné.[5]
1 Rassemblez vos données. Si vous apprenez cela pour un cours et que vous passez un test, vous pourriez recevoir un ensemble de chiffres prêts à l'emploi, par ex. 1, 4, 5, 7, 10. Ceci est votre ensemble de données - les numéros avec lesquels vous allez travailler. Toutefois, vous devrez peut-être organiser vous-même les numéros à partir d'un problème de table ou de mot. Assurez-vous que chaque numéro se rapporte au même genre de chose: par exemple, le nombre d'œufs dans chaque nid d'une population d'oiseaux donnée, ou le nombre de places de stationnement attachées à chaque maison sur un bloc donné.[5]  2 Organisez vos données en ordre croissant. En d'autres termes: arrangez les nombres du plus bas au plus haut. Répondez aux exemples suivants.
2 Organisez vos données en ordre croissant. En d'autres termes: arrangez les nombres du plus bas au plus haut. Répondez aux exemples suivants.  3 Diviser les données en deux. Pour ce faire, recherchez le point milieu de vos données: le ou les nombres au centre de l’ensemble. Si vous avez un nombre impair de nombres, choisissez le nombre exact exact. Si vous avez un nombre pair de nombres, le point milieu reposera entre les deux nombres intermédiaires.
3 Diviser les données en deux. Pour ce faire, recherchez le point milieu de vos données: le ou les nombres au centre de l’ensemble. Si vous avez un nombre impair de nombres, choisissez le nombre exact exact. Si vous avez un nombre pair de nombres, le point milieu reposera entre les deux nombres intermédiaires.  1 Trouvez la médiane de la moitié inférieure et supérieure de vos données. La médiane est le "milieu" ou le nombre qui est à mi-chemin dans un ensemble.[6] Dans ce cas, vous ne recherchez pas le milieu de l'ensemble, mais plutôt les points médians relatifs des sous-ensembles supérieur et inférieur. Si vous avez un nombre impair de données, n'incluez pas le chiffre du milieu - dans Set B, par exemple, vous ne figureriez pas dans l'un des 10.[7]
1 Trouvez la médiane de la moitié inférieure et supérieure de vos données. La médiane est le "milieu" ou le nombre qui est à mi-chemin dans un ensemble.[6] Dans ce cas, vous ne recherchez pas le milieu de l'ensemble, mais plutôt les points médians relatifs des sous-ensembles supérieur et inférieur. Si vous avez un nombre impair de données, n'incluez pas le chiffre du milieu - dans Set B, par exemple, vous ne figureriez pas dans l'un des 10.[7]  2 Soustraire Q3 - Q1 pour déterminer l'IQR. Vous savez maintenant combien de nombres se situent entre le 25e centile et le 75e centile. Vous pouvez l'utiliser pour comprendre la diffusion des données. Par exemple, si un test est noté sur 100 et que le QI des scores est de 5, vous pouvez supposer que la plupart des personnes qui le prennent ont une compréhension similaire du fait que la fourchette haute n'est pas très grande. Si le IQR des résultats des tests est de 30, cependant, vous pourriez commencer à vous demander pourquoi certaines personnes ont obtenu des résultats aussi élevés et d'autres si bas.
2 Soustraire Q3 - Q1 pour déterminer l'IQR. Vous savez maintenant combien de nombres se situent entre le 25e centile et le 75e centile. Vous pouvez l'utiliser pour comprendre la diffusion des données. Par exemple, si un test est noté sur 100 et que le QI des scores est de 5, vous pouvez supposer que la plupart des personnes qui le prennent ont une compréhension similaire du fait que la fourchette haute n'est pas très grande. Si le IQR des résultats des tests est de 30, cependant, vous pourriez commencer à vous demander pourquoi certaines personnes ont obtenu des résultats aussi élevés et d'autres si bas.