Un diagramme de boîte et de moustache est un diagramme qui montre la distribution statistique d'un ensemble de données. Cela permet de voir facilement comment les données sont distribuées sur une ligne numérique, et il est facile d'en créer une vous-même!
Pas
-
 1 Rassemblez vos données. Disons que nous commençons les chiffres 1, 3, 2, 4 et 5. Ceux-ci seront utilisés pour des exemples de calcul.
1 Rassemblez vos données. Disons que nous commençons les chiffres 1, 3, 2, 4 et 5. Ceux-ci seront utilisés pour des exemples de calcul. -
 2 Organiser les données du plus petit au plus grand. Prenez tous vos numéros et alignez-les dans l'ordre, de sorte que les plus petits nombres soient à gauche et les plus grands à droite. Dans notre cas, l'ordre des nombres est 1, 2, 3, 4 et 5.
2 Organiser les données du plus petit au plus grand. Prenez tous vos numéros et alignez-les dans l'ordre, de sorte que les plus petits nombres soient à gauche et les plus grands à droite. Dans notre cas, l'ordre des nombres est 1, 2, 3, 4 et 5. -
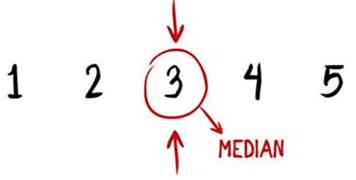 3 Trouvez la médiane de l'ensemble de données. La médiane est le nombre moyen dans un ensemble de données ordonné. (C'est pourquoi nous avons aligné tous les nombres à l'étape 2.) Pour les données de notre exemple, 3 est le nombre exactement au milieu et est donc notre médiane. La médiane est aussi appelée la deuxième quartile.
3 Trouvez la médiane de l'ensemble de données. La médiane est le nombre moyen dans un ensemble de données ordonné. (C'est pourquoi nous avons aligné tous les nombres à l'étape 2.) Pour les données de notre exemple, 3 est le nombre exactement au milieu et est donc notre médiane. La médiane est aussi appelée la deuxième quartile. - Dans un ensemble de données comportant un nombre impair de nombres, la médiane aura toujours le même nombre de chiffres de chaque côté. Pour l'ensemble de données 1, 2, 3, 4, 5, le nombre médian, 3, a 2 chiffres avant et 2 chiffres après. C'est comme ça qu'on peut être sûr que c'est notre médiane.
- Que se passe-t-il si le jeu de données avec lequel vous travaillez comporte un nombre pair de chiffres? Et si vous deviez trouver la médiane de 2, 4, 4, 7, 9, 10, 14, 15? Vous trouvez la médiane ici en prenant les deux nombres moyens et en trouvant leur moyenne. Dans notre exemple, vous prendrez 7 et 9 - les deux nombres intermédiaires - les additionnez et divisez-les par 2. 7 + 9 est égal à 16 et 16 divisé par 2 est égal à 8. La médiane de cet ensemble de données serait 8.
-
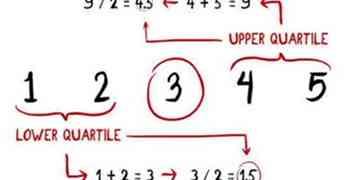 4 Trouvez les premier et troisième quartiles. Nous avons déjà trouvé le deuxième quartile de l'ensemble de données, qui est notre médiane. Maintenant, nous devons trouver la médiane de la moitié inférieure du jeu de données; dans notre exemple, ce serait la médiane des deux nombres à la la gauche de 3. La médiane de 1 et 2 est (1 + 2) / 2 = 1,5. Faites la même chose pour trouver la médiane des deux nombres à la droite de 3 (4 + 5) / 2 = 4,5.
4 Trouvez les premier et troisième quartiles. Nous avons déjà trouvé le deuxième quartile de l'ensemble de données, qui est notre médiane. Maintenant, nous devons trouver la médiane de la moitié inférieure du jeu de données; dans notre exemple, ce serait la médiane des deux nombres à la la gauche de 3. La médiane de 1 et 2 est (1 + 2) / 2 = 1,5. Faites la même chose pour trouver la médiane des deux nombres à la droite de 3 (4 + 5) / 2 = 4,5. -
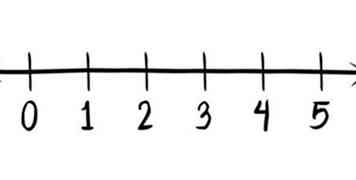 5 Dessine une ligne de tracé. Cela devrait être assez long pour contenir toutes vos données, plus un petit supplément de chaque côté. Assurez-vous de placer les numéros à intervalles réguliers. Si vous avez affaire à des nombres décimaux, tels que 4.5 et 1.5, assurez-vous de bien les étiqueter.
5 Dessine une ligne de tracé. Cela devrait être assez long pour contenir toutes vos données, plus un petit supplément de chaque côté. Assurez-vous de placer les numéros à intervalles réguliers. Si vous avez affaire à des nombres décimaux, tels que 4.5 et 1.5, assurez-vous de bien les étiqueter. - 6 Marquez vos premier, deuxième et troisième quartiles sur la ligne de tracé. Prenez les valeurs de vos premier, deuxième et troisième quartiles et marquez ces nombres sur la ligne de tracé. La marque doit être une ligne verticale à chaque quartile, en commençant légèrement au-dessus de la ligne de tracé.
-
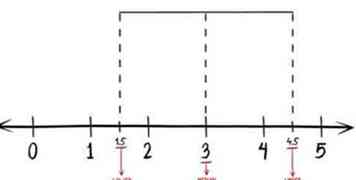 7 Faites une boîte en dessinant des lignes horizontales reliant les quartiles. Reliez le premier ou le premier quartile au haut du troisième quartile, en passant par le deuxième quartile. Connectez le bas du premier quartile au bas du troisième quartile, en vous assurant de passer par le deuxième quartile.
7 Faites une boîte en dessinant des lignes horizontales reliant les quartiles. Reliez le premier ou le premier quartile au haut du troisième quartile, en passant par le deuxième quartile. Connectez le bas du premier quartile au bas du troisième quartile, en vous assurant de passer par le deuxième quartile. -
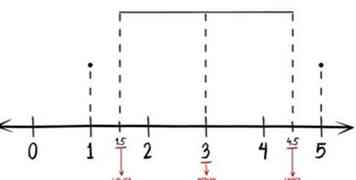 8 Marquez vos valeurs aberrantes. Recherchez le plus petit nombre, puis le plus grand, dans votre jeu de données et marquez-les sur la ligne de tracé. Marquez ces points avec un petit point. Dans le cas de notre exemple, la valeur la plus basse est 1 et la valeur la plus élevée est 5.
8 Marquez vos valeurs aberrantes. Recherchez le plus petit nombre, puis le plus grand, dans votre jeu de données et marquez-les sur la ligne de tracé. Marquez ces points avec un petit point. Dans le cas de notre exemple, la valeur la plus basse est 1 et la valeur la plus élevée est 5. -
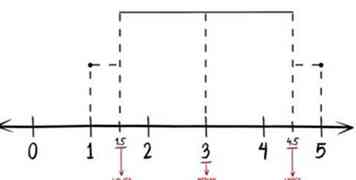 9 Connectez vos valeurs aberrantes à la boîte avec une ligne horizontale. La ligne droite qui relie les valeurs aberrantes s'appelle de manière informelle les "moustaches" de la boîte et du diagramme de moustaches.
9 Connectez vos valeurs aberrantes à la boîte avec une ligne horizontale. La ligne droite qui relie les valeurs aberrantes s'appelle de manière informelle les "moustaches" de la boîte et du diagramme de moustaches. - 10 Fini. Regardez une boîte et un diagramme de moustaches pour visualiser la distribution des nombres dans tout ensemble de données. Vous pouvez facilement voir, par exemple, si les nombres dans le jeu de données sont plus groupés dans le quartile supérieur en regardant la taille de la case supérieure, ainsi que la taille de la moustache supérieure. Les boîtes à moustaches et les moustaches sont une excellente alternative aux histogrammes et aux histogrammes.[1]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Rassemblez vos données. Disons que nous commençons les chiffres 1, 3, 2, 4 et 5. Ceux-ci seront utilisés pour des exemples de calcul.
1 Rassemblez vos données. Disons que nous commençons les chiffres 1, 3, 2, 4 et 5. Ceux-ci seront utilisés pour des exemples de calcul.  2 Organiser les données du plus petit au plus grand. Prenez tous vos numéros et alignez-les dans l'ordre, de sorte que les plus petits nombres soient à gauche et les plus grands à droite. Dans notre cas, l'ordre des nombres est 1, 2, 3, 4 et 5.
2 Organiser les données du plus petit au plus grand. Prenez tous vos numéros et alignez-les dans l'ordre, de sorte que les plus petits nombres soient à gauche et les plus grands à droite. Dans notre cas, l'ordre des nombres est 1, 2, 3, 4 et 5.  3 Trouvez la médiane de l'ensemble de données. La médiane est le nombre moyen dans un ensemble de données ordonné. (C'est pourquoi nous avons aligné tous les nombres à l'étape 2.) Pour les données de notre exemple, 3 est le nombre exactement au milieu et est donc notre médiane. La médiane est aussi appelée la deuxième quartile.
3 Trouvez la médiane de l'ensemble de données. La médiane est le nombre moyen dans un ensemble de données ordonné. (C'est pourquoi nous avons aligné tous les nombres à l'étape 2.) Pour les données de notre exemple, 3 est le nombre exactement au milieu et est donc notre médiane. La médiane est aussi appelée la deuxième quartile.  4 Trouvez les premier et troisième quartiles. Nous avons déjà trouvé le deuxième quartile de l'ensemble de données, qui est notre médiane. Maintenant, nous devons trouver la médiane de la moitié inférieure du jeu de données; dans notre exemple, ce serait la médiane des deux nombres à la la gauche de 3. La médiane de 1 et 2 est (1 + 2) / 2 = 1,5. Faites la même chose pour trouver la médiane des deux nombres à la droite de 3 (4 + 5) / 2 = 4,5.
4 Trouvez les premier et troisième quartiles. Nous avons déjà trouvé le deuxième quartile de l'ensemble de données, qui est notre médiane. Maintenant, nous devons trouver la médiane de la moitié inférieure du jeu de données; dans notre exemple, ce serait la médiane des deux nombres à la la gauche de 3. La médiane de 1 et 2 est (1 + 2) / 2 = 1,5. Faites la même chose pour trouver la médiane des deux nombres à la droite de 3 (4 + 5) / 2 = 4,5.  5 Dessine une ligne de tracé. Cela devrait être assez long pour contenir toutes vos données, plus un petit supplément de chaque côté. Assurez-vous de placer les numéros à intervalles réguliers. Si vous avez affaire à des nombres décimaux, tels que 4.5 et 1.5, assurez-vous de bien les étiqueter.
5 Dessine une ligne de tracé. Cela devrait être assez long pour contenir toutes vos données, plus un petit supplément de chaque côté. Assurez-vous de placer les numéros à intervalles réguliers. Si vous avez affaire à des nombres décimaux, tels que 4.5 et 1.5, assurez-vous de bien les étiqueter.  7 Faites une boîte en dessinant des lignes horizontales reliant les quartiles. Reliez le premier ou le premier quartile au haut du troisième quartile, en passant par le deuxième quartile. Connectez le bas du premier quartile au bas du troisième quartile, en vous assurant de passer par le deuxième quartile.
7 Faites une boîte en dessinant des lignes horizontales reliant les quartiles. Reliez le premier ou le premier quartile au haut du troisième quartile, en passant par le deuxième quartile. Connectez le bas du premier quartile au bas du troisième quartile, en vous assurant de passer par le deuxième quartile.  8 Marquez vos valeurs aberrantes. Recherchez le plus petit nombre, puis le plus grand, dans votre jeu de données et marquez-les sur la ligne de tracé. Marquez ces points avec un petit point. Dans le cas de notre exemple, la valeur la plus basse est 1 et la valeur la plus élevée est 5.
8 Marquez vos valeurs aberrantes. Recherchez le plus petit nombre, puis le plus grand, dans votre jeu de données et marquez-les sur la ligne de tracé. Marquez ces points avec un petit point. Dans le cas de notre exemple, la valeur la plus basse est 1 et la valeur la plus élevée est 5.  9 Connectez vos valeurs aberrantes à la boîte avec une ligne horizontale. La ligne droite qui relie les valeurs aberrantes s'appelle de manière informelle les "moustaches" de la boîte et du diagramme de moustaches.
9 Connectez vos valeurs aberrantes à la boîte avec une ligne horizontale. La ligne droite qui relie les valeurs aberrantes s'appelle de manière informelle les "moustaches" de la boîte et du diagramme de moustaches.