Le test t à deux échantillons est l'un des tests statistiques les plus couramment utilisés. Il est appliqué pour comparer si les moyennes de deux ensembles de données sont significativement différentes ou si leur différence est due uniquement au hasard. Il pourrait être utilisé pour déterminer si une nouvelle méthode d’enseignement a vraiment aidé à mieux former un groupe d’enfants ou si ce groupe est simplement plus intelligent. Ou, comme dans l'exemple ci-dessous, il pourrait être utilisé pour déterminer si les nouvelles voitures plus rapides utilisées pour livrer des pizzas ont vraiment aidé à accélérer les délais de livraison!
Pas
-
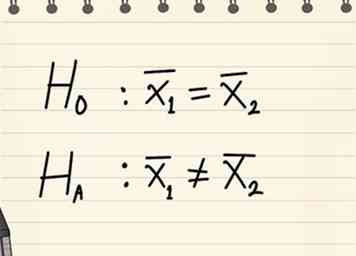 1 Déterminer une hypothèse nulle et alternative.
1 Déterminer une hypothèse nulle et alternative. - En général, l'hypothèse nulle indiquera que les deux populations testées n'ont pas de différence statistiquement significative.
- L'hypothèse alternative indiquera qu'il y a un présent.
-
 2 Déterminer un intervalle de confiance.
2 Déterminer un intervalle de confiance. - Nous appellerons cela le niveau alpha (α). La valeur typique est 0,05. Cela signifie qu'il y a 95% de confiance que la conclusion de ce test sera valide.
-
 3 Attribuez chaque population à l'un des deux ensembles de données.
3 Attribuez chaque population à l'un des deux ensembles de données. - Ces valeurs devront être distinctes lors de l'utilisation de l'équation.
-
 4 Détermine les valeurs n1 et n2.
4 Détermine les valeurs n1 et n2. - Celles-ci correspondent aux deux tailles d'échantillon ou au nombre de points de données dans chaque population.
-
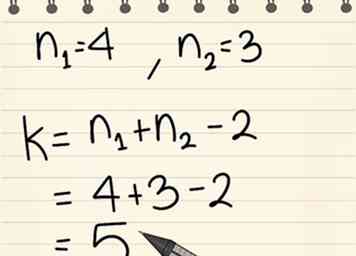 5 Détermine les degrés de liberté.
5 Détermine les degrés de liberté. - Nous appellerons cela la valeur k. Sur la table de distribution t ci-dessous, cette valeur est appelée df.
- Pour calculer cette valeur, ajoutez les deux valeurs n ensemble et soustrayez 2.
-
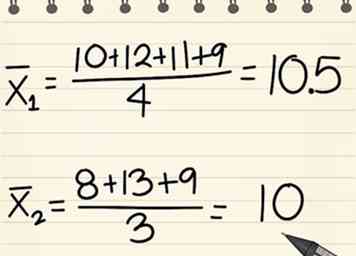 6 Déterminez les moyennes des deux jeux d'échantillons.
6 Déterminez les moyennes des deux jeux d'échantillons. - Nous les appellerons x̄1 et x̄2.
- Ceci est calculé en ajoutant tous les points de données de chaque ensemble d'échantillons, puis en divisant par le nombre de points de données dans l'ensemble (la valeur n correspondante).
-
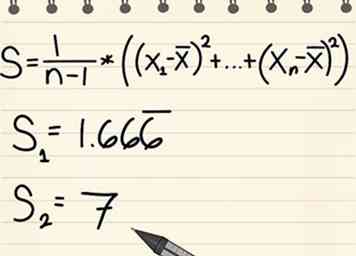 7 Déterminez les variances de chaque ensemble de données.
7 Déterminez les variances de chaque ensemble de données. - Nous les appellerons les valeurs S.
- Il s'agit d'un nombre décrivant la quantité de données variable dans son propre jeu d'échantillons. Utilisez la formule suivante.
-
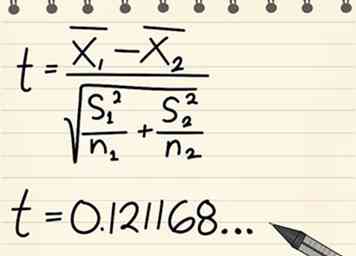 8 Calculez la statistique t en utilisant la formule suivante.
8 Calculez la statistique t en utilisant la formule suivante. -
 9 Utilisez les valeurs alpha et k pour trouver la valeur t critique sur la table t-distribution.
9 Utilisez les valeurs alpha et k pour trouver la valeur t critique sur la table t-distribution. -
 10 Comparez la valeur t critique et la statistique t calculée.
10 Comparez la valeur t critique et la statistique t calculée. - Si la statistique t calculée est supérieure à la valeur t critique, le test conclut à une différence statistiquement significative entre les deux populations.
- Par conséquent, vous rejetez l'hypothèse nulle selon laquelle il n'y a pas de différence statistiquement significative entre les deux populations.
- Dans tous les autres cas, il n'y a pas de différence statistiquement significative entre les deux populations.
- Le test ne parvient pas à rejeter l'hypothèse nulle.
- Si la statistique t calculée est supérieure à la valeur t critique, le test conclut à une différence statistiquement significative entre les deux populations.
-
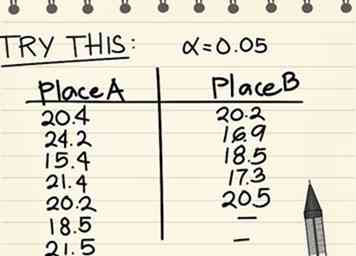 11 Utilisez l'exemple de problème suivant pour pratiquer les équations indiquées ci-dessus.
11 Utilisez l'exemple de problème suivant pour pratiquer les équations indiquées ci-dessus.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
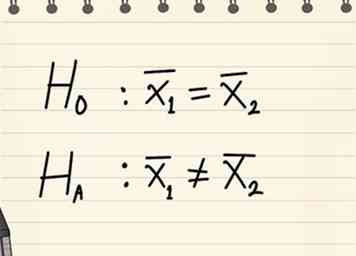 1 Déterminer une hypothèse nulle et alternative.
1 Déterminer une hypothèse nulle et alternative.  2 Déterminer un intervalle de confiance.
2 Déterminer un intervalle de confiance.  3 Attribuez chaque population à l'un des deux ensembles de données.
3 Attribuez chaque population à l'un des deux ensembles de données.  4 Détermine les valeurs n1 et n2.
4 Détermine les valeurs n1 et n2. 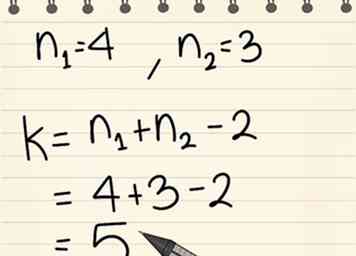 5 Détermine les degrés de liberté.
5 Détermine les degrés de liberté. 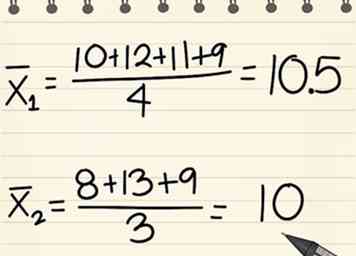 6 Déterminez les moyennes des deux jeux d'échantillons.
6 Déterminez les moyennes des deux jeux d'échantillons. 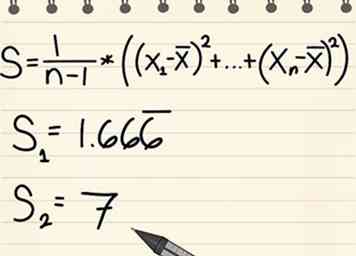 7 Déterminez les variances de chaque ensemble de données.
7 Déterminez les variances de chaque ensemble de données. 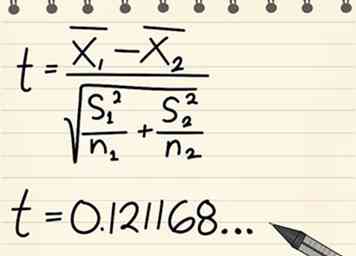 8 Calculez la statistique t en utilisant la formule suivante.
8 Calculez la statistique t en utilisant la formule suivante.  9 Utilisez les valeurs alpha et k pour trouver la valeur t critique sur la table t-distribution.
9 Utilisez les valeurs alpha et k pour trouver la valeur t critique sur la table t-distribution.  10 Comparez la valeur t critique et la statistique t calculée.
10 Comparez la valeur t critique et la statistique t calculée.  11 Utilisez l'exemple de problème suivant pour pratiquer les équations indiquées ci-dessus.
11 Utilisez l'exemple de problème suivant pour pratiquer les équations indiquées ci-dessus.