Les cartes de contrôle sont un moyen efficace d'analyser les données de performance pour évaluer un processus. Les cartes de contrôle ont de nombreuses utilisations. ils peuvent être utilisés dans la fabrication pour tester si les machines produisent des produits conformes aux spécifications. En outre, ils ont de nombreuses applications simples telles que les professeurs qui les utilisent pour évaluer les résultats des tests. Pour créer une carte de contrôle, il est utile d’avoir Excel; cela vous simplifiera la vie.

Pas

  1. 1 Vérifiez que vos données répondent aux critères suivants:
    • Les données devraient normalement être distribuées autour d'une moyenne (moyenne).
      • Dans l'exemple ci-dessous, un fabricant de bouteilles remplit ses bouteilles à 16 oz. (signifier); ils évaluent si leur processus est «in-control». La quantité en onces de plus de 16 oz. est normalement distribué autour de la moyenne.
    • Les mesures doivent être indépendantes les unes des autres.
      • Dans l'exemple, les mesures sont en sous-groupes. Les données dans les sous-groupes doivent être indépendantes du numéro de mesure; chaque point de données aura un sous-groupe et un numéro de mesure.
  2. 2 Trouvez la moyenne de chaque sous-groupe.
    • Pour trouver la moyenne, ajoutez toutes les mesures dans le sous-groupe et divisez par le nombre de mesures dans le sous-groupe.
      • Dans l'exemple, il y a 20 sous-groupes et dans chaque sous-groupe, il y a 4 mesures.
  3. 3 Trouvez la moyenne de tous les moyens de l'étape précédente (X).
    • Cela vous donnera la moyenne globale de tous les points de données.
    • La moyenne globale sera la ligne centrale dans le graphique (CL), qui est de 13,75 pour notre exemple.
  4. 4 Calculez l'écart type (S) des points de données (voir les conseils).
  5. 5 Calculez les limites de contrôle supérieure et inférieure (UCL, LCL) en utilisant la formule suivante:
    • UCL = CL + 3 * S
    • LCL = CL - 3 * S
    • La formule représente respectivement 3 écarts-types et 3 écarts-types inférieurs à la moyenne.
  6. 6 Reportez-vous au tableau ci-dessous avec les étapes 7 à 10.
  7. 7 Tracez une ligne à chaque déviation.
    • Dans l'exemple ci-dessus, il y a une ligne tracée à un, deux et trois écarts types (sigma) en dehors de la moyenne.
      • La zone C est à 1 sigma de la moyenne (vert).
      • La zone B est à 2 sigma de la moyenne (jaune).
      • La zone A est à 3 sigma de la moyenne (rouge).
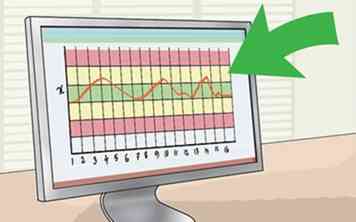  8. 8 Représentez graphiquement le diagramme de contrôle X-bar en représentant graphiquement les moyennes des sous-groupes (axe des abscisses) vers les mesures (axe des ordonnées). Votre graphique devrait ressembler à ceci:
  9. 9 Évaluez le graphique pour voir si le processus est hors de contrôle. Le graphique est hors de contrôle si l'une des conditions suivantes est vraie:
    • Tout point tombe au-delà de la zone rouge (au-dessus ou au-dessous de la ligne 3-sigma).
    • 8 points consécutifs tombent d'un côté de la ligne médiane.
    • 2 des 3 points consécutifs tombent dans la zone A.
    • 4 des 5 points consécutifs tombent dans la zone A et / ou la zone B.
    • 15 points consécutifs sont dans la zone C.
    • 8 points consécutifs non dans la zone C.
  10. 10 Indiquez si le système est sous contrôle ou hors de contrôle.

Exemples de graphiques de contrôle

Exemple de tableau de contrôle Exemple de graphique de contrôle pour les sous-groupes Exemple de graphique de contrôle pour plusieurs groupes