Trouver la surface d'une boîte est facile tant que vous connaissez la longueur des côtés. Une fois que vous connaissez la longueur des côtés, il vous suffit de les brancher sur une équation de base pour obtenir votre réponse. Vous pouvez même trouver la surface de boîtes cylindriques avec quelques mesures simples.
Méthode One of Three:
Boîtes Rectangulaires
-
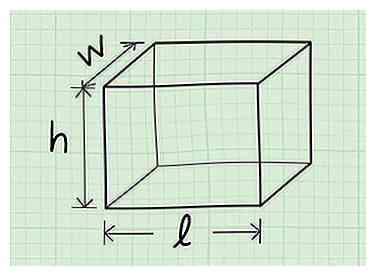
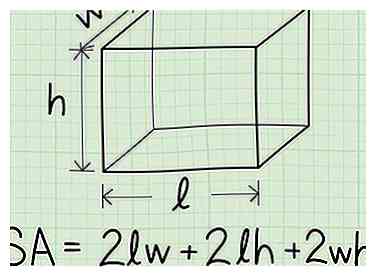 1 Ajouter la zone de chaque côté pour obtenir la surface de la boîte. La surface est la surface totale de chaque côté. Tant que vous savez trouver la zone d'un rectangle régulier, qui est simplement la longueur multipliée par la hauteur, vous pouvez trouver chaque côté et les ajouter ensemble. Cependant, il existe également une formule simplifiée qui le fera pour vous si vous connaissez les dimensions de la boîte:
1 Ajouter la zone de chaque côté pour obtenir la surface de la boîte. La surface est la surface totale de chaque côté. Tant que vous savez trouver la zone d'un rectangle régulier, qui est simplement la longueur multipliée par la hauteur, vous pouvez trouver chaque côté et les ajouter ensemble. Cependant, il existe également une formule simplifiée qui le fera pour vous si vous connaissez les dimensions de la boîte: - l est la longueur de la boîte, ou du côté le plus long.
- h est la hauteur de la boîte.
- w est la largeur de la boîte.
-
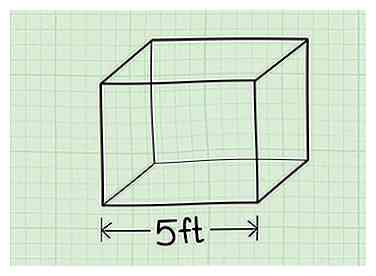 2 Mesurer la longueur de la boîte. C'est votre côté le plus long. Il devrait y avoir 4 lignes identiques de même longueur sur toute la boîte. Posez la boîte sur son côté le plus long pour le rendre plus facile à mesurer.
2 Mesurer la longueur de la boîte. C'est votre côté le plus long. Il devrait y avoir 4 lignes identiques de même longueur sur toute la boîte. Posez la boîte sur son côté le plus long pour le rendre plus facile à mesurer. - Exemple: La longueur de la boîte est de 5 pieds.
-
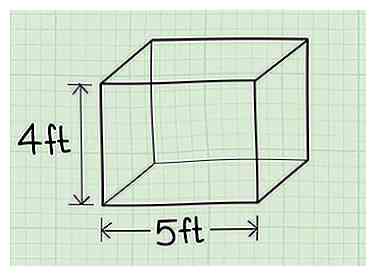 3 Mesurez la hauteur de la boîte ou la distance entre le sol et le haut. Assurez-vous de ne pas mesurer le même côté que la longueur.
3 Mesurez la hauteur de la boîte ou la distance entre le sol et le haut. Assurez-vous de ne pas mesurer le même côté que la longueur. - Exemple: La hauteur de la boîte est de 4 pieds.
-
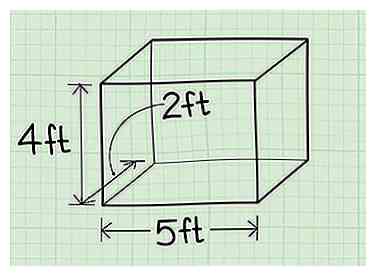 4 Mesurer la largeur de la boîte. C'est le côté directement perpendiculaire (il forme un angle droit ou L) avec la longueur. Assurez-vous de ne pas remesurer la hauteur.
4 Mesurer la largeur de la boîte. C'est le côté directement perpendiculaire (il forme un angle droit ou L) avec la longueur. Assurez-vous de ne pas remesurer la hauteur. - Exemple: La largeur de la boîte est de 2 pieds.
-
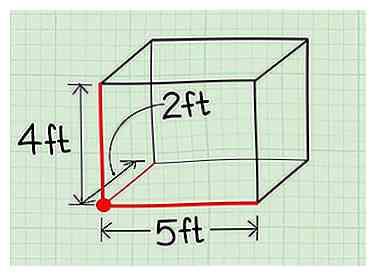 5 Assurez-vous de ne pas mesurer le même côté deux fois. Le moyen le plus simple d’éviter cela est de vérifier que les trois lignes se rencontrent à un moment donné. Trouvez un coin et mesurez les trois côtés qui en sortent - ceci vous garantit d'avoir les bonnes mesures.
5 Assurez-vous de ne pas mesurer le même côté deux fois. Le moyen le plus simple d’éviter cela est de vérifier que les trois lignes se rencontrent à un moment donné. Trouvez un coin et mesurez les trois côtés qui en sortent - ceci vous garantit d'avoir les bonnes mesures. - Les côtés peuvent être la même mesure. Vous voulez juste vous assurer de mesurer trois côtés uniques, même si deux ou trois d’entre eux sont tous identiques.
-
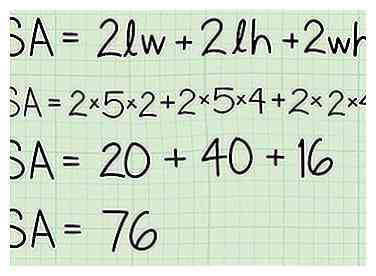 6 Entrez vos mesures dans la formule pour résoudre l'équation. Une fois que vous avez les chiffres, le reste est facile. Entrez simplement les mesures et ajoutez-les.
6 Entrez vos mesures dans la formule pour résoudre l'équation. Une fois que vous avez les chiffres, le reste est facile. Entrez simplement les mesures et ajoutez-les. -
 7 Exprimez votre réponse en "unités au carré" lorsque vous avez terminé. Cela permet aux gens de savoir comment vous avez tout mesuré et constitue une partie cruciale de votre réponse. Heureusement, tout ce que vous avez à faire est d'utiliser les unités fournies dans la question. Pour cet exemple, puisque les unités étaient en pieds, vous mettriez "pieds carrés" à la fin de votre réponse:
7 Exprimez votre réponse en "unités au carré" lorsque vous avez terminé. Cela permet aux gens de savoir comment vous avez tout mesuré et constitue une partie cruciale de votre réponse. Heureusement, tout ce que vous avez à faire est d'utiliser les unités fournies dans la question. Pour cet exemple, puisque les unités étaient en pieds, vous mettriez "pieds carrés" à la fin de votre réponse: - Vous avez une boîte de 5 pieds de long, 4 pieds de haut et 2 pieds de large, quelle est la surface totale?
- Répondre:
-
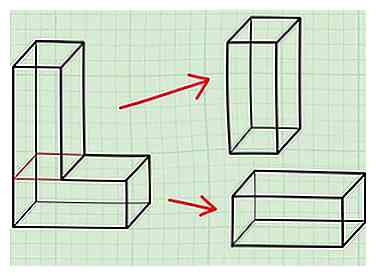 8 Casser les boîtes complexes en morceaux plus petits pour trouver la surface. Par exemple, disons que vous avez une boîte en forme de "L". Au lieu de tout trouver à la main, pensez simplement à deux boîtes distinctes, la moitié verticale en haut et la moitié horizontale en bas. Trouvez la surface des deux, puis ajoutez-les ensemble pour obtenir la surface totale.[1] Par exemple, si vous avez une boîte en forme de U:
8 Casser les boîtes complexes en morceaux plus petits pour trouver la surface. Par exemple, disons que vous avez une boîte en forme de "L". Au lieu de tout trouver à la main, pensez simplement à deux boîtes distinctes, la moitié verticale en haut et la moitié horizontale en bas. Trouvez la surface des deux, puis ajoutez-les ensemble pour obtenir la surface totale.[1] Par exemple, si vous avez une boîte en forme de U: - Disons que le fond a une superficie de 12 unités au carré.
- Disons que les deux côtés ont une superficie de 15 unités au carré.
- La surface totale serait 42 unités au carré, depuis .
Méthode deux sur trois:
Boîtes cylindriques (tubes)
-
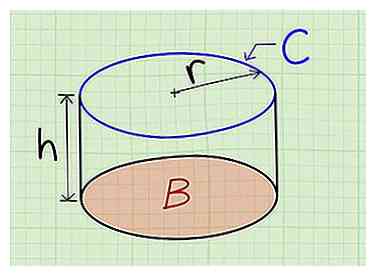
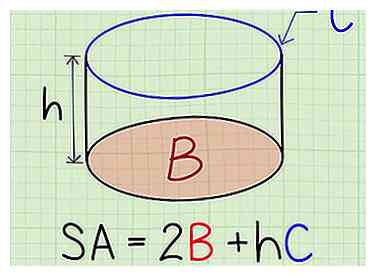 1 Ajouter la surface des bases à la hauteur fois la circonférence pour trouver la surface d'un cylindre. Cela ne fonctionne qu'avec les cylindres droits, ce qui signifie qu'ils ne sont pas inclinés. La formule appropriée est
1 Ajouter la surface des bases à la hauteur fois la circonférence pour trouver la surface d'un cylindre. Cela ne fonctionne qu'avec les cylindres droits, ce qui signifie qu'ils ne sont pas inclinés. La formule appropriée est Par exemple, si l'aire de la base est 3, la hauteur est 5, et la circonférence est 6, quelle est la surface? Réponse = 36 unités au carré. - B est la zone de la base.
- h est la hauteur du cylindre.
- C est la circonférence de la base.[2]
-
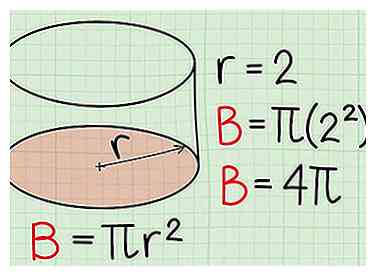 2 Trouvez la zone de la base. La base est l'extrémité circulaire du cylindre. On peut le trouver avec la formule
2 Trouvez la zone de la base. La base est l'extrémité circulaire du cylindre. On peut le trouver avec la formule R est le rayon du cercle. Pi est la constante, arrondie à 3.14 pour les problèmes simples. Vous pouvez également le laisser comme "pi" si vous n'avez pas de calculatrice. - Exemple: Le rayon de la base dans un cylindre est 2. Quelle est l'aire de la base?
- B =
-
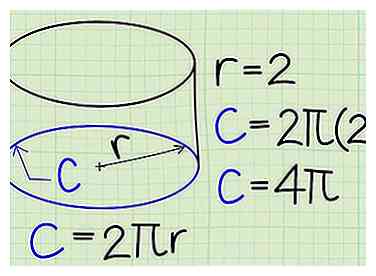 3 Calculez la circonférence si la base. La circonférence est la distance autour du bord du cercle. On le trouve avec la formule
3 Calculez la circonférence si la base. La circonférence est la distance autour du bord du cercle. On le trouve avec la formule En continuant l'exemple précédent: - C =
-
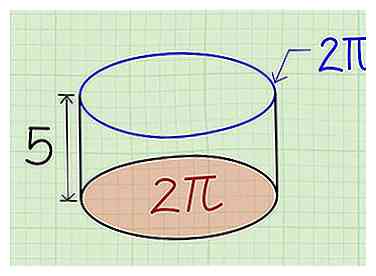 4 Trouvez la hauteur du cylindre en mesurant l'espace entre les deux bases. La hauteur d'un cylindre est juste une autre façon de déterminer combien de temps c'est. C'est la ligne droite entre le centre des deux bases.
4 Trouvez la hauteur du cylindre en mesurant l'espace entre les deux bases. La hauteur d'un cylindre est juste une autre façon de déterminer combien de temps c'est. C'est la ligne droite entre le centre des deux bases. - Exemple: Dans le même cylindre, de rayon 2 pouces, la hauteur est de 5 pouces.
-
 5 Entrez vos plus petites pièces dans la formule pour trouver votre surface. Une fois que vous avez votre surface de base, votre circonférence et votre hauteur, il vous suffit de brancher les chiffres dans votre formule pour obtenir la bonne réponse.
5 Entrez vos plus petites pièces dans la formule pour trouver votre surface. Une fois que vous avez votre surface de base, votre circonférence et votre hauteur, il vous suffit de brancher les chiffres dans votre formule pour obtenir la bonne réponse. -
 6 Exprimez votre réponse en unités au carré. Tous les problèmes de surface nécessitent des unités pour leur donner de l’échelle. La zone est-elle en pouces ou en pieds, par exemple. Les unités correspondent toujours aux unités qui vous ont été données dans le problème. Si aucune unité n’est donnée, vous devez simplement écrire la phrase "unités au carré" ou ""
6 Exprimez votre réponse en unités au carré. Tous les problèmes de surface nécessitent des unités pour leur donner de l’échelle. La zone est-elle en pouces ou en pieds, par exemple. Les unités correspondent toujours aux unités qui vous ont été données dans le problème. Si aucune unité n’est donnée, vous devez simplement écrire la phrase "unités au carré" ou "" - Dans l'exemple, les unités ont été données en pouces. Donc, la réponse finale serait [3]
Méthode trois sur trois:
Problèmes de pratique
-
 1 Essayez des problèmes pratiques avec des rectangles. Pour voir les réponses, mettez en surbrillance juste après la flèche:
1 Essayez des problèmes pratiques avec des rectangles. Pour voir les réponses, mettez en surbrillance juste après la flèche: - L = 10, W = 3, H = 2, → 112 unités carrées
- L = 6,2, W = 2, H = 5,4 → 113,36 unités au carré
- Sur une boîte rectangulaire, le haut est 5x3x2, le bas 6x2x2. → 118pi unités carrées
-
 2 Essayez des problèmes pratiques avec les cylindres. Pour voir les réponses, mettez en surbrillance après la flèche:
2 Essayez des problèmes pratiques avec les cylindres. Pour voir les réponses, mettez en surbrillance après la flèche: - Base = 3, Hauteur = 10, Circonférence = 1,5 → 21 unités au carré
- Base = 25pi, Hauteur = 3, Circonférence = 10pi →80pi unités carrées
- Rayon = 3, hauteur = 3 → 36pi unités au carré
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Ajouter la zone de chaque côté pour obtenir la surface de la boîte. La surface est la surface totale de chaque côté. Tant que vous savez trouver la zone d'un rectangle régulier, qui est simplement la longueur multipliée par la hauteur, vous pouvez trouver chaque côté et les ajouter ensemble. Cependant, il existe également une formule simplifiée qui le fera pour vous si vous connaissez les dimensions de la boîte:
1 Ajouter la zone de chaque côté pour obtenir la surface de la boîte. La surface est la surface totale de chaque côté. Tant que vous savez trouver la zone d'un rectangle régulier, qui est simplement la longueur multipliée par la hauteur, vous pouvez trouver chaque côté et les ajouter ensemble. Cependant, il existe également une formule simplifiée qui le fera pour vous si vous connaissez les dimensions de la boîte:  2 Mesurer la longueur de la boîte. C'est votre côté le plus long. Il devrait y avoir 4 lignes identiques de même longueur sur toute la boîte. Posez la boîte sur son côté le plus long pour le rendre plus facile à mesurer.
2 Mesurer la longueur de la boîte. C'est votre côté le plus long. Il devrait y avoir 4 lignes identiques de même longueur sur toute la boîte. Posez la boîte sur son côté le plus long pour le rendre plus facile à mesurer.  3 Mesurez la hauteur de la boîte ou la distance entre le sol et le haut. Assurez-vous de ne pas mesurer le même côté que la longueur.
3 Mesurez la hauteur de la boîte ou la distance entre le sol et le haut. Assurez-vous de ne pas mesurer le même côté que la longueur.  4 Mesurer la largeur de la boîte. C'est le côté directement perpendiculaire (il forme un angle droit ou L) avec la longueur. Assurez-vous de ne pas remesurer la hauteur.
4 Mesurer la largeur de la boîte. C'est le côté directement perpendiculaire (il forme un angle droit ou L) avec la longueur. Assurez-vous de ne pas remesurer la hauteur.  5 Assurez-vous de ne pas mesurer le même côté deux fois. Le moyen le plus simple d’éviter cela est de vérifier que les trois lignes se rencontrent à un moment donné. Trouvez un coin et mesurez les trois côtés qui en sortent - ceci vous garantit d'avoir les bonnes mesures.
5 Assurez-vous de ne pas mesurer le même côté deux fois. Le moyen le plus simple d’éviter cela est de vérifier que les trois lignes se rencontrent à un moment donné. Trouvez un coin et mesurez les trois côtés qui en sortent - ceci vous garantit d'avoir les bonnes mesures. 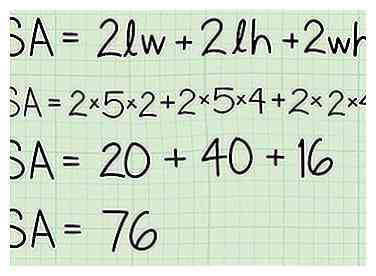 6 Entrez vos mesures dans la formule pour résoudre l'équation. Une fois que vous avez les chiffres, le reste est facile. Entrez simplement les mesures et ajoutez-les.
6 Entrez vos mesures dans la formule pour résoudre l'équation. Une fois que vous avez les chiffres, le reste est facile. Entrez simplement les mesures et ajoutez-les.  7 Exprimez votre réponse en "unités au carré" lorsque vous avez terminé. Cela permet aux gens de savoir comment vous avez tout mesuré et constitue une partie cruciale de votre réponse. Heureusement, tout ce que vous avez à faire est d'utiliser les unités fournies dans la question. Pour cet exemple, puisque les unités étaient en pieds, vous mettriez "pieds carrés" à la fin de votre réponse:
7 Exprimez votre réponse en "unités au carré" lorsque vous avez terminé. Cela permet aux gens de savoir comment vous avez tout mesuré et constitue une partie cruciale de votre réponse. Heureusement, tout ce que vous avez à faire est d'utiliser les unités fournies dans la question. Pour cet exemple, puisque les unités étaient en pieds, vous mettriez "pieds carrés" à la fin de votre réponse:  8 Casser les boîtes complexes en morceaux plus petits pour trouver la surface. Par exemple, disons que vous avez une boîte en forme de "L". Au lieu de tout trouver à la main, pensez simplement à deux boîtes distinctes, la moitié verticale en haut et la moitié horizontale en bas. Trouvez la surface des deux, puis ajoutez-les ensemble pour obtenir la surface totale.[1] Par exemple, si vous avez une boîte en forme de U:
8 Casser les boîtes complexes en morceaux plus petits pour trouver la surface. Par exemple, disons que vous avez une boîte en forme de "L". Au lieu de tout trouver à la main, pensez simplement à deux boîtes distinctes, la moitié verticale en haut et la moitié horizontale en bas. Trouvez la surface des deux, puis ajoutez-les ensemble pour obtenir la surface totale.[1] Par exemple, si vous avez une boîte en forme de U:  1 Ajouter la surface des bases à la hauteur fois la circonférence pour trouver la surface d'un cylindre. Cela ne fonctionne qu'avec les cylindres droits, ce qui signifie qu'ils ne sont pas inclinés. La formule appropriée est
1 Ajouter la surface des bases à la hauteur fois la circonférence pour trouver la surface d'un cylindre. Cela ne fonctionne qu'avec les cylindres droits, ce qui signifie qu'ils ne sont pas inclinés. La formule appropriée est  2 Trouvez la zone de la base. La base est l'extrémité circulaire du cylindre. On peut le trouver avec la formule
2 Trouvez la zone de la base. La base est l'extrémité circulaire du cylindre. On peut le trouver avec la formule  3 Calculez la circonférence si la base. La circonférence est la distance autour du bord du cercle. On le trouve avec la formule
3 Calculez la circonférence si la base. La circonférence est la distance autour du bord du cercle. On le trouve avec la formule  4 Trouvez la hauteur du cylindre en mesurant l'espace entre les deux bases. La hauteur d'un cylindre est juste une autre façon de déterminer combien de temps c'est. C'est la ligne droite entre le centre des deux bases.
4 Trouvez la hauteur du cylindre en mesurant l'espace entre les deux bases. La hauteur d'un cylindre est juste une autre façon de déterminer combien de temps c'est. C'est la ligne droite entre le centre des deux bases.  5 Entrez vos plus petites pièces dans la formule pour trouver votre surface. Une fois que vous avez votre surface de base, votre circonférence et votre hauteur, il vous suffit de brancher les chiffres dans votre formule pour obtenir la bonne réponse.
5 Entrez vos plus petites pièces dans la formule pour trouver votre surface. Une fois que vous avez votre surface de base, votre circonférence et votre hauteur, il vous suffit de brancher les chiffres dans votre formule pour obtenir la bonne réponse.  6 Exprimez votre réponse en unités au carré. Tous les problèmes de surface nécessitent des unités pour leur donner de l’échelle. La zone est-elle en pouces ou en pieds, par exemple. Les unités correspondent toujours aux unités qui vous ont été données dans le problème. Si aucune unité n’est donnée, vous devez simplement écrire la phrase "unités au carré" ou "
6 Exprimez votre réponse en unités au carré. Tous les problèmes de surface nécessitent des unités pour leur donner de l’échelle. La zone est-elle en pouces ou en pieds, par exemple. Les unités correspondent toujours aux unités qui vous ont été données dans le problème. Si aucune unité n’est donnée, vous devez simplement écrire la phrase "unités au carré" ou " 1 Essayez des problèmes pratiques avec des rectangles. Pour voir les réponses, mettez en surbrillance juste après la flèche:
1 Essayez des problèmes pratiques avec des rectangles. Pour voir les réponses, mettez en surbrillance juste après la flèche:  2 Essayez des problèmes pratiques avec les cylindres. Pour voir les réponses, mettez en surbrillance après la flèche:
2 Essayez des problèmes pratiques avec les cylindres. Pour voir les réponses, mettez en surbrillance après la flèche: