La surface d'un cône est la somme de la surface latérale et de la surface de base. Si vous connaissez le rayon de la base et l'inclinaison du cône, vous pouvez facilement trouver la surface totale en utilisant une formule standard. Parfois, cependant, vous pouvez avoir le rayon et une autre mesure, comme la hauteur ou le volume du cône. Dans ces cas, vous pouvez utiliser le théorème de Pythagore et la formule du volume pour obtenir la hauteur de la pente, et donc la surface du cône.
Méthode One of Three:
Si vous connaissez le rayon et la hauteur de l'inclinaison
-
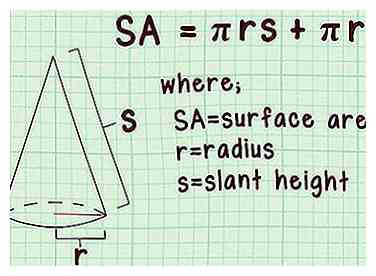 1 Configurez la formule pour la surface du cône. La formule est , où est égal à la surface du cône, est égal à la longueur du rayon de la base du cône, et est égal à la hauteur oblique du cône.[1]
1 Configurez la formule pour la surface du cône. La formule est , où est égal à la surface du cône, est égal à la longueur du rayon de la base du cône, et est égal à la hauteur oblique du cône.[1] - La surface totale d'un cône est égale à la somme de la surface latérale () et la surface de base (), puisque la base d’un cône est un cercle.
- La hauteur inclinée est la distance diagonale entre le sommet supérieur du cône et le bord de la base.[2]
- Assurez-vous de ne pas confondre la «hauteur de la taille» avec la «hauteur», qui correspond à la distance perpendiculaire entre le sommet supérieur et la base.[3]
-
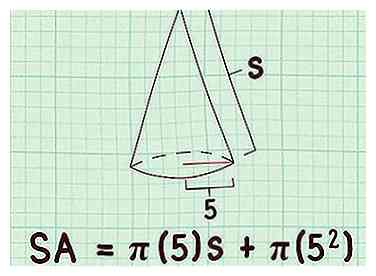 2 Branchez la valeur du rayon dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer. Assurez-vous de remplacer les deux variables dans la formule.
2 Branchez la valeur du rayon dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer. Assurez-vous de remplacer les deux variables dans la formule. - Par exemple, si le rayon de la base d'un cône est de 5 cm, votre formule ressemblera à ceci: .
-
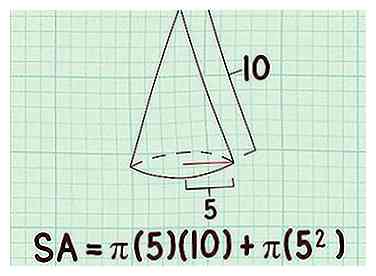 3 Branchez la valeur de la hauteur d'inclinaison dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer.
3 Branchez la valeur de la hauteur d'inclinaison dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer. - Par exemple, si la hauteur oblique d'un cône est de 10 cm, votre formule ressemblera à ceci: .
-
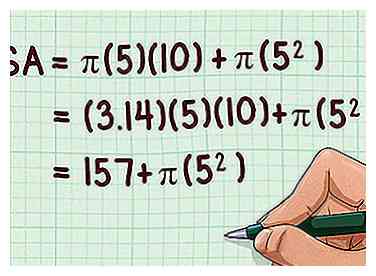 4 Calculer la surface latérale du cône (). Pour ce faire, multipliez le rayon, la hauteur d'inclinaison et . Si vous n'utilisez pas de calculatrice, utilisez 3.14 comme valeur de .
4 Calculer la surface latérale du cône (). Pour ce faire, multipliez le rayon, la hauteur d'inclinaison et . Si vous n'utilisez pas de calculatrice, utilisez 3.14 comme valeur de . - Par exemple:
- Par exemple:
-
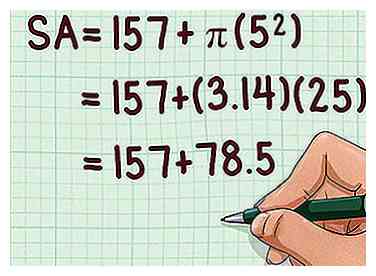 5 Calculer l'aire de la base du cône (). Pour ce faire, placez le rayon de la base, puis multipliez-le par . Si vous n'utilisez pas de calculatrice, utilisez 3.14 comme valeur de .
5 Calculer l'aire de la base du cône (). Pour ce faire, placez le rayon de la base, puis multipliez-le par . Si vous n'utilisez pas de calculatrice, utilisez 3.14 comme valeur de . - Par exemple:
- Par exemple:
-
 6 Ajouter la surface latérale et la surface de base du cône. Cela vous donnera la surface totale du cône, en unités carrées.
6 Ajouter la surface latérale et la surface de base du cône. Cela vous donnera la surface totale du cône, en unités carrées. - Par exemple:
Ainsi, la surface d'un cône d'un rayon de 5 cm et d'une hauteur inclinée de 10 cm est de 235,5 centimètres carrés.
- Par exemple:
Méthode deux sur trois:
Si vous connaissez le rayon et la hauteur perpendiculaire
-
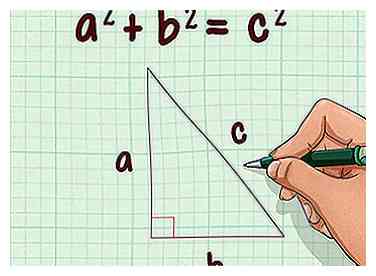 1 Configurez la formule du théorème de Pythagore. La formule est , où et égale les longueurs latérales d'un triangle rectangle, et est égal à la longueur de l'hypoténuse (le côté opposé à l'angle droit).[4]
1 Configurez la formule du théorème de Pythagore. La formule est , où et égale les longueurs latérales d'un triangle rectangle, et est égal à la longueur de l'hypoténuse (le côté opposé à l'angle droit).[4] - Assurez-vous de ne pas confondre la hauteur du cône avec la hauteur oblique, qui correspond à la distance diagonale entre le sommet supérieur du cône et le bord de la base.[5]
- La hauteur est la distance perpendiculaire entre le sommet supérieur et la base.[6]
-
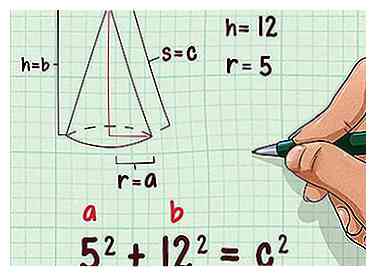 2 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable et la hauteur de la variable .
2 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable et la hauteur de la variable . - Par exemple, si le rayon d'un cône est de 5 cm et la hauteur de 12 cm, votre formule ressemblera à ceci: .
-
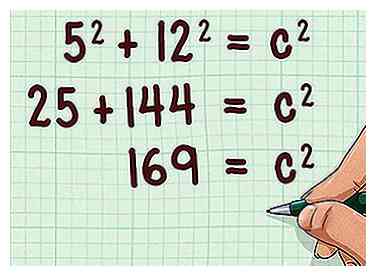 3 Carrez les longueurs du rayon et de la hauteur, puis ajoutez. Rappelez-vous que la quadrature d'un nombre signifie le multiplier par lui-même.
3 Carrez les longueurs du rayon et de la hauteur, puis ajoutez. Rappelez-vous que la quadrature d'un nombre signifie le multiplier par lui-même. - Par exemple:
- Par exemple:
-
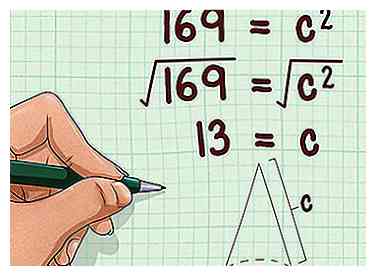 4 Prenez la racine carrée de chaque côté de l'équation. Cela vous donnera la longueur de l'hypoténuse du triangle rectangle, qui est égale à la hauteur oblique du cône.[7]
4 Prenez la racine carrée de chaque côté de l'équation. Cela vous donnera la longueur de l'hypoténuse du triangle rectangle, qui est égale à la hauteur oblique du cône.[7] - Par exemple:
La hauteur inclinée du cône est donc de 13 cm.
- Par exemple:
-
 5 Configurez la formule pour la surface du cône. La formule est , où est égal à la surface du cône, est égal à la longueur du rayon de la base du cône, et est égal à la hauteur oblique du cône.[8]
5 Configurez la formule pour la surface du cône. La formule est , où est égal à la surface du cône, est égal à la longueur du rayon de la base du cône, et est égal à la hauteur oblique du cône.[8] - La surface totale d'un cône est égale à la somme de la surface latérale () et la surface de base (, puisque la base d'un cône est un cercle.
-
 6 Branchez toutes les valeurs connues dans la formule. Le rayon doit être donné, et vous avez déjà calculé la hauteur d'inclinaison. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour
6 Branchez toutes les valeurs connues dans la formule. Le rayon doit être donné, et vous avez déjà calculé la hauteur d'inclinaison. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour - Par exemple, pour un cône d'un rayon de 5 cm et d'une hauteur oblique de 13 cm, votre formule ressemblera à ceci: .
-
 7 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées.
7 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées. - Par exemple:
Ainsi, la surface d'un cône d'un rayon de 5 cm et d'une hauteur de 12 cm est de 282,6 centimètres carrés.
- Par exemple:
Méthode trois sur trois:
Si vous connaissez le rayon et le volume
-
 1 Configurez la formule pour le volume d'un cône. La formule est , où est égal au volume du cône, est égal au rayon de la base du cône, et est égal à la hauteur perpendiculaire du cône.[9]
1 Configurez la formule pour le volume d'un cône. La formule est , où est égal au volume du cône, est égal au rayon de la base du cône, et est égal à la hauteur perpendiculaire du cône.[9] - Assurez-vous de ne pas confondre la hauteur du cône avec la hauteur oblique, qui correspond à la distance diagonale entre le sommet supérieur du cône et le bord de la base.[10]
- La hauteur est la distance perpendiculaire entre le sommet supérieur et la base.[11]
-
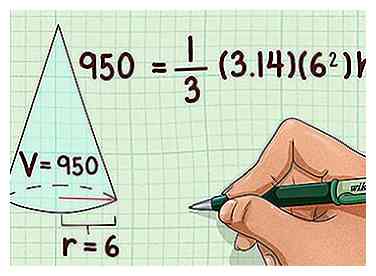 2 Branchez les valeurs connues dans la formule. Vous devez connaître le volume et la longueur du rayon. Sinon, vous ne pouvez pas utiliser cette méthode. Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour .
2 Branchez les valeurs connues dans la formule. Vous devez connaître le volume et la longueur du rayon. Sinon, vous ne pouvez pas utiliser cette méthode. Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour . - Par exemple, si vous savez qu'un cône a un volume de 950 centimètres cubes et un rayon de 6 centimètres, votre formule ressemblera à ceci: .
-
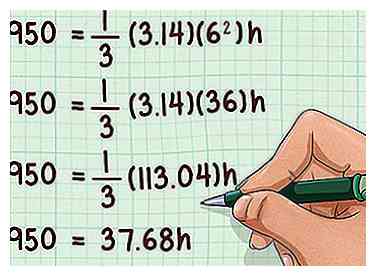 3 Terminez la multiplication. Tout d'abord, placez le rayon au carré, puis multipliez cette valeur par . Ensuite, multipliez ce produit par . Cela vous donnera le coefficient pour le variable.
3 Terminez la multiplication. Tout d'abord, placez le rayon au carré, puis multipliez cette valeur par . Ensuite, multipliez ce produit par . Cela vous donnera le coefficient pour le variable. - Par exemple:
- Par exemple:
-
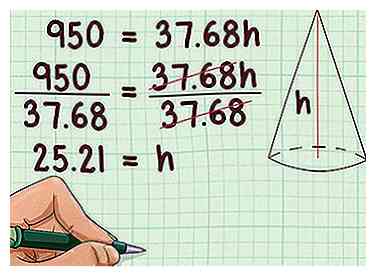 4 Diviser chaque côté par le coefficient. Cela vous donnera la valeur de , qui est la hauteur perpendiculaire du cône. Vous aurez besoin de cette information pour trouver l'inclinaison du cône, ce qui est nécessaire pour déterminer la surface.
4 Diviser chaque côté par le coefficient. Cela vous donnera la valeur de , qui est la hauteur perpendiculaire du cône. Vous aurez besoin de cette information pour trouver l'inclinaison du cône, ce qui est nécessaire pour déterminer la surface. - Par exemple:
Donc, la hauteur du cône est de 25,21 cm.
- Par exemple:
-
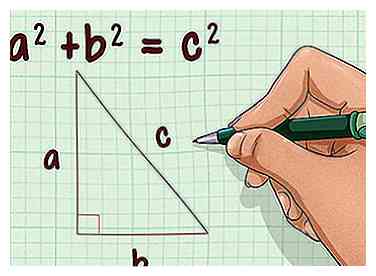 5 Configurez la formule du théorème de Pythagore. La formule est , où et égale les longueurs latérales d'un triangle rectangle, et est égal à la longueur de l'hypoténuse (le côté opposé à l'angle droit).[12]
5 Configurez la formule du théorème de Pythagore. La formule est , où et égale les longueurs latérales d'un triangle rectangle, et est égal à la longueur de l'hypoténuse (le côté opposé à l'angle droit).[12] -
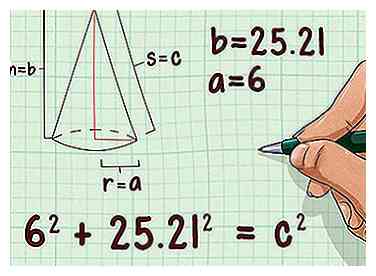 6 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable et la hauteur de la variable
6 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable et la hauteur de la variable - Par exemple, si le rayon d'un cône est de 6 cm et la hauteur de 25,21 cm, votre formule ressemblera à ceci: .
-
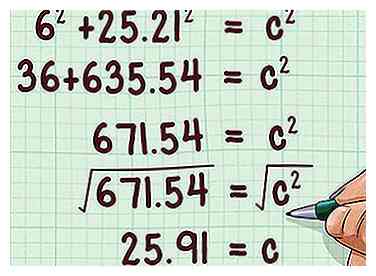 7 Résoudre pour . Cela vous donnera la longueur de l'hypoténuse du triangle rectangle, qui est également la hauteur oblique du cône.
7 Résoudre pour . Cela vous donnera la longueur de l'hypoténuse du triangle rectangle, qui est également la hauteur oblique du cône. - Par exemple:
La hauteur inclinée du cône est donc de 25,91 cm.
- Par exemple:
-
 8 Configurez la formule pour la surface du cône. La formule est , où est égal à la surface du cône, est égal à la longueur du rayon de la base du cône, et est égal à la hauteur oblique du cône.[13]
8 Configurez la formule pour la surface du cône. La formule est , où est égal à la surface du cône, est égal à la longueur du rayon de la base du cône, et est égal à la hauteur oblique du cône.[13] - La surface totale d'un cône est égale à la somme de la surface latérale () et la surface de base (, puisque la base d'un cône est un cercle.
-
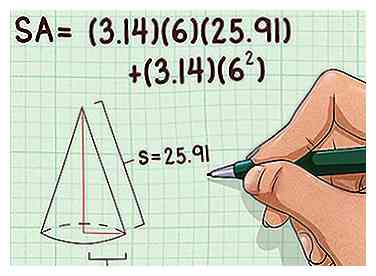 9 Branchez toutes les valeurs connues dans la formule. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour
9 Branchez toutes les valeurs connues dans la formule. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour - Par exemple, pour un cône d'un rayon de 6 cm et d'une hauteur oblique de 25,91 cm, votre formule ressemblera à ceci: .
-
 10 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées.
10 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées. - Par exemple:
Ainsi, la surface d'un cône d'un rayon de 6 centimètres et d'un volume de 950 centimètres cubes est de 601,18 centimètres carrés.
- Par exemple:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Configurez la formule pour la surface du cône. La formule est
1 Configurez la formule pour la surface du cône. La formule est  2 Branchez la valeur du rayon dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer. Assurez-vous de remplacer les deux
2 Branchez la valeur du rayon dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer. Assurez-vous de remplacer les deux  3 Branchez la valeur de la hauteur d'inclinaison dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer.
3 Branchez la valeur de la hauteur d'inclinaison dans la formule. Cette longueur devrait être donnée ou vous devriez pouvoir la mesurer. 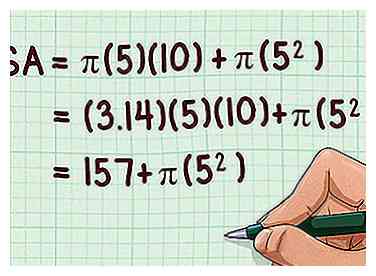 4 Calculer la surface latérale du cône (
4 Calculer la surface latérale du cône (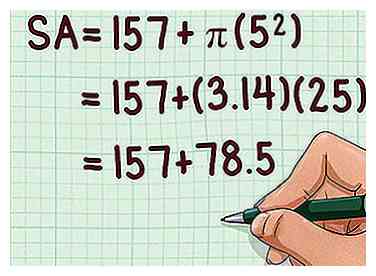 5 Calculer l'aire de la base du cône (
5 Calculer l'aire de la base du cône ( 6 Ajouter la surface latérale et la surface de base du cône. Cela vous donnera la surface totale du cône, en unités carrées.
6 Ajouter la surface latérale et la surface de base du cône. Cela vous donnera la surface totale du cône, en unités carrées. 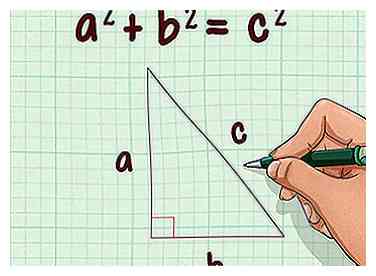 1 Configurez la formule du théorème de Pythagore. La formule est
1 Configurez la formule du théorème de Pythagore. La formule est 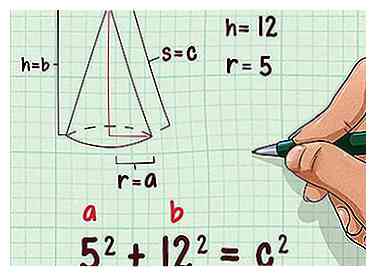 2 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable
2 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable 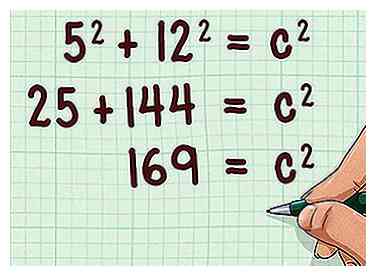 3 Carrez les longueurs du rayon et de la hauteur, puis ajoutez. Rappelez-vous que la quadrature d'un nombre signifie le multiplier par lui-même.
3 Carrez les longueurs du rayon et de la hauteur, puis ajoutez. Rappelez-vous que la quadrature d'un nombre signifie le multiplier par lui-même. 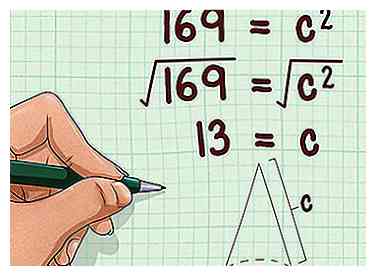 4 Prenez la racine carrée de chaque côté de l'équation. Cela vous donnera la longueur de l'hypoténuse du triangle rectangle, qui est égale à la hauteur oblique du cône.[7]
4 Prenez la racine carrée de chaque côté de l'équation. Cela vous donnera la longueur de l'hypoténuse du triangle rectangle, qui est égale à la hauteur oblique du cône.[7]  5 Configurez la formule pour la surface du cône. La formule est
5 Configurez la formule pour la surface du cône. La formule est  6 Branchez toutes les valeurs connues dans la formule. Le rayon doit être donné, et vous avez déjà calculé la hauteur d'inclinaison. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour
6 Branchez toutes les valeurs connues dans la formule. Le rayon doit être donné, et vous avez déjà calculé la hauteur d'inclinaison. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour  7 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées.
7 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées.  1 Configurez la formule pour le volume d'un cône. La formule est
1 Configurez la formule pour le volume d'un cône. La formule est 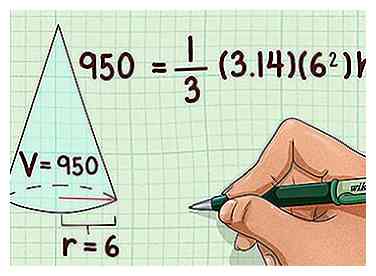 2 Branchez les valeurs connues dans la formule. Vous devez connaître le volume et la longueur du rayon. Sinon, vous ne pouvez pas utiliser cette méthode. Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour
2 Branchez les valeurs connues dans la formule. Vous devez connaître le volume et la longueur du rayon. Sinon, vous ne pouvez pas utiliser cette méthode. Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour 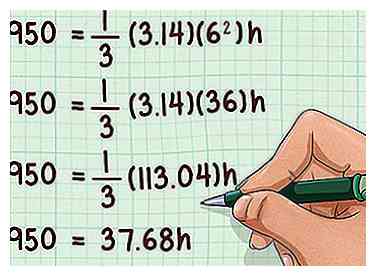 3 Terminez la multiplication. Tout d'abord, placez le rayon au carré, puis multipliez cette valeur par
3 Terminez la multiplication. Tout d'abord, placez le rayon au carré, puis multipliez cette valeur par 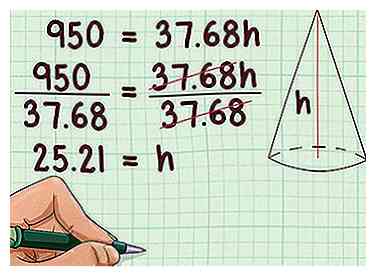 4 Diviser chaque côté par le
4 Diviser chaque côté par le  5 Configurez la formule du théorème de Pythagore. La formule est
5 Configurez la formule du théorème de Pythagore. La formule est 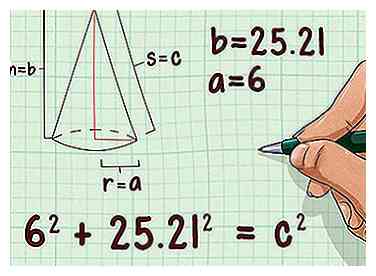 6 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable
6 Branchez la longueur du rayon et la hauteur dans la formule. Vous utiliserez le rayon et la hauteur du cône comme les deux côtés d'un triangle rectangle. Remplacer le rayon pour la variable 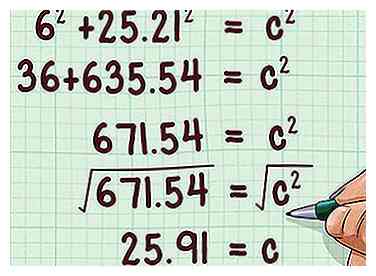 7 Résoudre pour
7 Résoudre pour  8 Configurez la formule pour la surface du cône. La formule est
8 Configurez la formule pour la surface du cône. La formule est 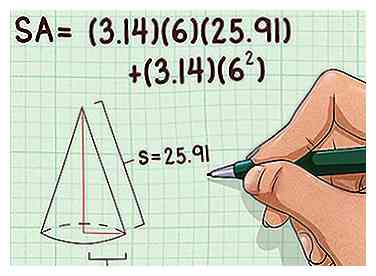 9 Branchez toutes les valeurs connues dans la formule. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour
9 Branchez toutes les valeurs connues dans la formule. Assurez-vous d'utiliser la hauteur d'inclinaison dans la formule de la surface et non la hauteur (perpendiculaire). Si vous n'utilisez pas de calculatrice, utilisez 3.14 pour  10 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées.
10 Multipliez pour trouver la zone latérale et la zone de base. Ensuite, ajoutez ces produits ensemble. La somme vous donnera la surface totale du cône en unités carrées.