Comment trouver une surface

La surface est la quantité totale d'espace occupée par toutes les surfaces d'un objet. C'est la somme de la surface de toutes les surfaces de cet objet.^[1] Trouver la surface d'une forme tridimensionnelle est relativement facile tant que vous connaissez la bonne formule. Chaque forme a sa propre formule distincte, vous devez donc d'abord identifier la forme avec laquelle vous travaillez. La mémorisation de la formule de surface pour différents objets peut faciliter les calculs à l’avenir. Voici quelques-unes des formes les plus courantes que vous pourriez rencontrer.

Méthode 1 sur 7:
cube

1. 1 Définissez la formule pour la surface d'un cube. Un cube a six côtés carrés identiques. Parce que la longueur et la largeur d'un carré sont égales, l'aire d'un carré est une², où une est la longueur d'un côté. Puisqu'il y a 6 côtés identiques d'un cube, pour trouver la surface, multipliez simplement la surface d'un côté fois 6. La formule pour la surface (SA) d'un cube est SA = 6a², où une est la longueur d'un côté.^[2]
   • Les unités de surface seront une unité de longueur au carré:², cm², m², etc.
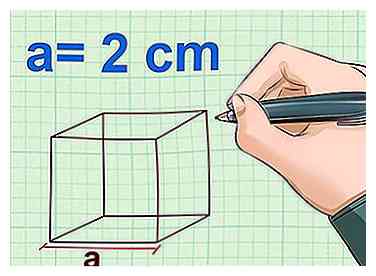2. 2 Mesurer la longueur d'un côté. Chaque côté ou arête d'un cube doit, par définition, être de même longueur que les autres, il suffit donc de mesurer un côté. À l'aide d'une règle, mesurez la longueur du côté. Faites attention aux unités que vous utilisez.
   • Marquez cette mesure comme une.
   • Exemple: a = 2 cm
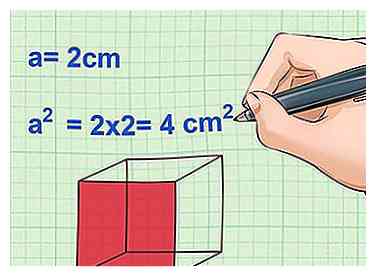3. 3 Carrez votre mesure pour une. Carré la mesure prise pour la longueur du bord. Carrer une mesure signifie la multiplier par elle-même. Lorsque vous commencez à apprendre ces formules, il peut être utile de les écrire comme suit: SA = 6 * a * a.
   • Notez que cette étape calcule la surface d'un côté du cube.
   • Exemple: a = 2 cm
   • une² = 2 x 2 = 4 cm²
4. 4 Multipliez ce produit par six. Rappelez-vous qu'un cube a six côtés identiques. Maintenant que vous avez la zone d'un côté, vous devez la multiplier par six pour tenir compte des six côtés.
   • Cette étape complète le calcul de la surface du cube.
   • Exemple: une² = 4 cm²
   • Surface = 6 x a² = 6 x 4 = 24 cm²

Méthode deux sur sept:
Prisme rectangulaire

1. 1 Définir la formule pour la surface sont d'un prisme rectangulaire. Comme un cube, un prisme rectangulaire a six côtés, mais contrairement à un cube, les côtés ne sont pas identiques. Dans un prisme rectangulaire, seuls les côtés opposés sont égaux.^[3] De ce fait, la surface d'un prisme rectangulaire doit prendre en compte les différentes longueurs latérales de la formule SA = 2ab + 2bc + 2ac.
   • Pour cette formule, une est égal à la largeur du prisme, b est égal à la hauteur, et c est égal à la longueur.
   • En décomposant la formule, vous pouvez voir que vous additionnez simplement toutes les zones de chaque face de l'objet.
   • Les unités de surface seront une unité de longueur au carré:², cm², m², etc.
2. 2 Mesurer la longueur, la hauteur et la largeur de chaque côté. Les trois mesures peuvent varier, il faut donc les prendre séparément. À l'aide d'une règle, mesurez chaque côté et notez-le. Utilisez les mêmes unités pour chaque mesure.
   • Mesurez la longueur de la base pour déterminer la longueur du prisme et affectez-la à c.
   • Exemple: c = 5 cm
   • Mesurer la largeur de la base pour déterminer la largeur du prisme et attribuer ceci à une.
   • Exemple: a = 2 cm
   • Mesurer la hauteur du côté pour déterminer la hauteur du prisme et attribuer ceci à b.
   • Exemple: b = 3 cm
3. 3 Calculer l'aire de l'un des côtés du prisme, puis multiplier par deux. Rappelez-vous, il y a 6 faces d'un prisme rectangulaire, mais les côtés opposés sont identiques. Multipliez la longueur et la hauteur, ou c et une pour trouver l'aire d'un visage. Prenez cette mesure et multipliez-la par deux pour tenir compte du côté identique opposé.^[4]
   • Exemple: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm²
4. 4 Trouvez la zone de l’autre côté du prisme et multipliez par deux. Comme pour la première paire de faces, multipliez la largeur et la hauteur, ou une et b pour trouver l'aire d'une autre face du prisme. Multipliez cette mesure par deux pour tenir compte des côtés identiques opposés.^[5]
   • Exemple: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm²
5. 5 Calculer l'aire des extrémités du prisme et multiplier par deux. Les deux dernières faces du prisme seront les extrémités. Multipliez la longueur et la largeur, ou c et b pour trouver leur région. Multipliez cette mesure par deux pour tenir compte des deux côtés.^[6]
   • Exemple: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm²
6. 6 Ajoutez les trois mesures distinctes ensemble. Étant donné que la surface est la surface totale de toutes les faces d'un objet, la dernière étape consiste à ajouter toutes les zones calculées individuellement. Ajouter les mesures de surface pour tous les côtés afin de trouver la surface totale.^[7]
   • Exemple: Surface = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm².

Méthode trois sur sept:
Prisme triangulaire

1. 1 Définissez la formule de surface pour un prisme triangulaire. Un prisme triangulaire a deux côtés triangulaires identiques et trois faces rectangulaires. Pour trouver la surface, vous devez calculer la surface de tous les côtés et les ajouter ensemble. La surface d'un prisme triangulaire est SA = 2A + PH, où A est la surface de la base triangulaire, P est le périmètre de la base triangulaire et h est la hauteur du prisme.^[8]
   • Pour cette formule, UNE est l'aire d'un triangle qui est A = 1 / 2bh où b est la base du triangle et h est la hauteur.
   • P est simplement le périmètre du triangle calculé en additionnant les trois côtés du triangle.
   • Les unités de surface seront une unité de longueur au carré:², cm², m², etc.
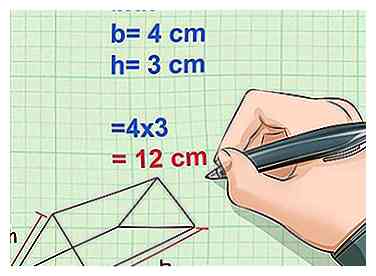2. 2 Calculer l'aire de la face triangulaire et multiplier par deux. La zone d'un triangle est ¹/₂b * h où b est la base du triangle et h la hauteur. Comme il existe deux faces de triangle identiques, nous pouvons multiplier la formule par deux. Cela rend le calcul pour les deux faces simplement, b * h.^[9]
   • La base, b, équivaut à la longueur du bas du triangle.
   • Exemple: b = 4 cm
   • La hauteur, h, de la base triangulaire égale la distance entre le bord inférieur et le sommet supérieur.
   • Exemple: h = 3 cm
   • Superficie du triangle multipliée par 2 = 2 (1/2) b * h = b * h = 4 * 3 = 12 cm
3. 3 Mesurez chaque côté du triangle et la hauteur du prisme. Pour terminer le calcul de la surface, vous devez connaître la longueur de chaque côté du triangle et la hauteur du prisme. La hauteur est la distance entre les deux faces triangulaires.
   • Exemple: H = 5 cm
   • Les trois côtés se réfèrent aux trois côtés de la base triangulaire.
   • Exemple: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm
4. 4 Détermine le périmètre du triangle. Le périmètre du triangle peut être calculé simplement en additionnant tous les côtés mesurés: S1 + S2 + S3.
   • Exemple: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm
5. 5 Multipliez le périmètre de la base par la hauteur du prisme. Rappelez-vous que la hauteur du prisme est la distance entre les deux bases triangulaires. En d'autres termes, multiplier P par H.
   • Exemple: P x H = 12 x 5 = 60 cm²
6. 6 Ajoutez les deux mesures distinctes ensemble. Vous devrez ajouter les deux mesures des deux étapes précédentes pour calculer la surface du prisme triangulaire.^[10]
   • Exemple: 2A + PH = 12 + 60 = 72 cm².

Méthode quatre sur sept:
Sphère

1. 1 Définir la formule de surface pour une sphère. Une sphère a une surface courbe et la surface doit donc utiliser la constante mathématique, pi. La surface d'une sphère est donnée par l'équation SA = 4π * r².^[11]
   • Pour cette formule, r est égal au rayon de la sphère. Pi, ou π, devrait être approximé à 3.14.
   • Les unités de surface seront une unité de longueur au carré:², cm², m², etc.
2. 2 Mesurer le rayon de la sphère. Le rayon de la sphère est la moitié du diamètre ou la moitié de la distance d'un côté du centre de la sphère à l'autre.^[12]
   • Exemple: r = 3 cm
3. 3 Carrez le rayon. Pour arrondir un nombre, il suffit de le multiplier par lui-même. Multipliez la mesure pour r par lui-même. Rappelez-vous que cette formule peut être réécrite sous la forme SA = 4π * r * r.^[13]
   • Exemple: r² = r x r = 3 x 3 = 9 cm²
4. 4 Multipliez le rayon carré par une approximation de pi. Pi est une constante qui représente le rapport entre la circonférence d'un cercle et son diamètre.^[14] C'est un nombre irrationnel qui a beaucoup de chiffres décimaux. Il est fréquemment estimé à 3.14. Multipliez le rayon carré par π, ou 3,14, pour trouver l'aire d'une section circulaire de la sphère.^[15]
   • Exemple: π * r² = 3,14 x 9 = 28,26 cm²
5. 5 Multipliez ce produit par quatre. Pour compléter le calcul, multipliez par 4. Trouvez la surface de la sphère en multipliant la surface circulaire plate par quatre.^[16]
   • Exemple: 4π * r² = 4 x 28,26 = 113,04 cm²

Méthode cinq sur sept:
Cylindre

1. 1 Définir la formule de surface pour un cylindre. Un cylindre a deux extrémités circulaires entourant une surface arrondie. La formule pour la surface d'un cylindre est SA = 2π * r² + 2π * rh, où r est égal au rayon de la base circulaire et h est égal à la hauteur du cylindre. Rond pi ou π à 3.14.^[17]
   • 2π * r² représente la surface des deux extrémités circulaires tandis que 2πrh est la surface de la colonne reliant les deux extrémités.
   • Les unités de surface seront une unité de longueur au carré:², cm², m², etc.
2. 2 Mesurer le rayon et la hauteur du cylindre. Le rayon d'un cercle est la moitié du diamètre ou la moitié de la distance d'un côté du centre du cercle à l'autre.^[18] La hauteur est la distance totale du cylindre de bout en bout. À l'aide d'une règle, prenez ces mesures et notez-les.
   • Exemple: r = 3 cm
   • Exemple: h = 5 cm
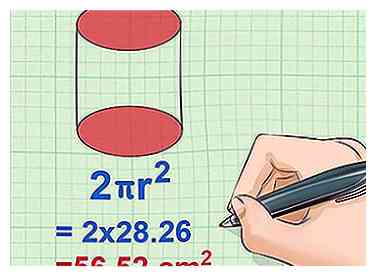3. 3 Trouvez l'aire de la base et multipliez par deux. Pour trouver l'aire de la base, utilisez simplement la formule pour l'aire du cercle ou π * r². Pour compléter le calcul, placez le rayon et multipliez par pi. Multipliez par deux pour tenir compte du deuxième cercle identique à l'autre extrémité du cylindre.^[19]
   • Exemple: Zone de base = π * r² = 3,14 x 3 x 3 = 28,26 cm²
   • Exemple: 2π * r² = 2 x 28,26 = 56,52 cm²
4. 4 Calculer la surface du cylindre lui-même, en utilisant 2π * rh. C'est la formule pour calculer la surface d'un tube. Le tube est l'espace entre les deux extrémités circulaires du cylindre. Multipliez le rayon par deux, piet la hauteur.^[20]
   • Exemple: 2π * rh = 2 x 3,14 x 3 x 5 = 94,2 cm²
5. 5 Ajoutez les deux mesures distinctes ensemble. Ajoutez la surface des deux cercles à la surface de l’espace entre les deux cercles pour calculer la surface totale du cylindre.Notez que l'ajout de ces deux pièces vous permet de reconnaître la formule originale: SA = 2π * r² + 2π * rh.^[21]
   • Exemple: 2π * r² + 2π * rh = 56,52 + 94,2 = 150,72 cm²

Méthode six sur sept:
Pyramide carrée

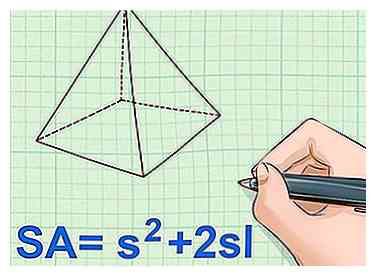1. 1 Définissez la formule de surface pour une pyramide carrée. Une pyramide carrée a une base carrée et quatre côtés triangulaires. Rappelez-vous que l'aire du carré correspond à la longueur d'un côté au carré. L'aire d'un triangle est 1 / 2sl (côté du triangle multiplié par la longueur ou la hauteur du triangle). Comme il y a quatre triangles, pour trouver la surface totale, vous devez multiplier par quatre. L'ajout de toutes ces faces permet d'obtenir l'équation de la surface d'une pyramide carrée: SA = s² + 2sl.^[22]
   • Pour cette équation, s se réfère à la longueur de chaque côté de la base carrée et l se réfère à la hauteur oblique de chaque côté triangulaire.
   • Les unités de surface seront une unité de longueur au carré:², cm², m², etc.
2. 2 Mesurer la hauteur et le côté de la base. La hauteur oblique, l, est la hauteur de l'un des côtés triangulaires. C'est la distance entre la base et le sommet de la pyramide, mesurée le long d'un côté plat. Le côté de base, s, est la longueur d'un côté de la base carrée. Comme la base est carrée, cette mesure est la même pour tous les côtés. Utilisez une règle pour effectuer chaque mesure.^[23]
   • Exemple: l = 3 cm
   • Exemple: s = 1 cm
3. 3 Trouvez la zone de la base carrée. L'aire d'une base carrée peut être calculée en quadrillant la longueur d'un côté ou en multipliant s par lui-même.^[24]
   • Exemple: s² = s x s = 1 x 1 = 1 cm²
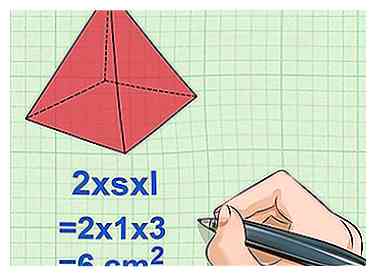4. 4 Calculez l'aire totale des quatre faces triangulaires. La seconde partie de l'équation concerne la surface des quatre côtés triangulaires restants. En utilisant la formule 2ls, multipliez s par l et deux. Cela vous permettra de trouver la zone de chaque côté.^[25]
   • Exemple: 2 x s x l = 2 x 1 x 3 = 6 cm²
5. 5 Ajoutez les deux zones distinctes ensemble. Ajoutez la surface totale des côtés à la zone de la base pour calculer la surface totale.^[26]
   • Exemple: s² + 2sl = 1 + 6 = 7 cm²

Méthode Seven of Seven:
Cône

1. 1 Définir la formule de surface pour un cône. Un cône a une base circulaire et une surface arrondie qui se termine en pointe. Pour trouver la surface, vous devez calculer l'aire de la base circulaire et la surface du cône et les ajouter ensemble. La formule pour la surface d'un cône est la suivante: SA = π * r² + π * rl, où r est le rayon de la base circulaire, l est la hauteur oblique du cône et π est la constante mathématique pi (3.14).^[27]
   • Les unités de surface seront une unité de longueur au carré:², cm², m², etc.
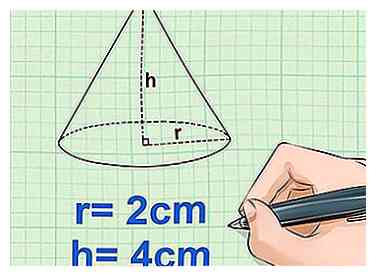2. 2 Mesurer le rayon et la hauteur du cône. Le rayon est la distance entre le centre de la base circulaire et le côté de la base. La hauteur est la distance entre le centre de la base et le sommet du cône, mesurée par le centre du cône.^[28]
   • Exemple: r = 2 cm
   • Exemple: h = 4 cm
3. 3 Calculer la hauteur d'inclinaison (l) du cône. Parce que la hauteur oblique est en fait l'hypoténuse d'un triangle, vous devez utiliser le théorème de Pythagore pour le calculer. Utilisez la forme réarrangée, l = √ (r² + h²), où r est le rayon et h est la hauteur du cône. ^[29]
   • Exemple: l = √ (r² + h²) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm
4. 4 Détermine l'aire de la base circulaire. L'aire de la base est calculée avec la formule π * r². Après avoir mesuré le rayon, placez-le (multipliez-le par lui-même), puis multipliez ce produit par pi.^[30]
   • Exemple: π * r² = 3,14 x 2 x 2 = 12,56 cm²
5. 5 Calculez la surface du haut du cône. En utilisant la formule π * rl, où r est le rayon du cercle et l est la hauteur d'inclinaison précédemment calculée, vous pouvez trouver la surface de la partie supérieure du cône.^[31]
   • Exemple: π * rl = 3,14 x 2 x 4,47 = 28,07 cm
6. 6 Ajouter deux zones ensemble pour trouver la surface totale. Calculez la surface finale de votre cône en ajoutant l'aire de la base circulaire au calcul de l'étape précédente.^[32]
   • Exemple: π * r² + π * rl = 12,56 + 28,07 = 40,63 cm²