La surface d'une sphère est le nombre d'unités (cm, pouces, pieds - quelle que soit votre mesure) qui recouvrent l'extérieur d'un objet sphérique. Découvert par le philosophe et mathématicien grec Aristote il y a des milliers d'années, l'équation est relativement simple, même si ses origines ne le sont pas. Pour trouver la surface d'une sphère, utilisez la formule (4πr2), où r = le rayon du cercle.
Pas
-
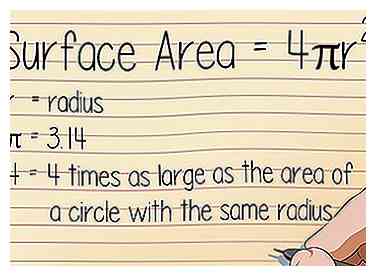 1 Connaître les parties de l'équation, Surface Surface = 4πr2. Cette formule presque ancienne reste la manière la plus simple de déterminer la surface d'une sphère. En utilisant presque n'importe quelle calculatrice, vous pouvez brancher le rayon pour obtenir la surface de votre sphère.
1 Connaître les parties de l'équation, Surface Surface = 4πr2. Cette formule presque ancienne reste la manière la plus simple de déterminer la surface d'une sphère. En utilisant presque n'importe quelle calculatrice, vous pouvez brancher le rayon pour obtenir la surface de votre sphère. - r ou "rayon: Le rayon est la distance entre le centre de la sphère et le bord de cette sphère.
- π ou "pi:" Ce nombre incroyable (équivalant approximativement à 3,14) représente le rapport entre la circonférence et le diamètre d'un cercle et est utile dans toutes les équations comportant des cercles et des sphères. Il est généralement raccourci de π = 3,1416, mais il existe un nombre infini de décimales.[1]
- 4: Pour des raisons assez complexes, la surface d'une sphère est toujours 4 fois plus grande que l'aire d'un cercle de même rayon.
-
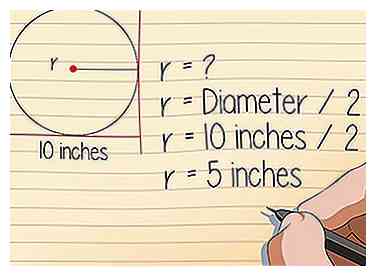 2 Trouve le rayon de la sphère. Parfois, votre problème vous fournira le rayon, et d'autres fois vous devrez le trouver vous-même. Si on vous donne le diamètre d'un cercle, divisez simplement le diamètre par 2 pour obtenir le rayon. Par exemple, une sphère de diamètre 10 pouces a un rayon de 5 pouces.
2 Trouve le rayon de la sphère. Parfois, votre problème vous fournira le rayon, et d'autres fois vous devrez le trouver vous-même. Si on vous donne le diamètre d'un cercle, divisez simplement le diamètre par 2 pour obtenir le rayon. Par exemple, une sphère de diamètre 10 pouces a un rayon de 5 pouces. - Astuce avancée:Si vous ne connaissez que le volume d'une sphère, vous devez faire un peu plus de travail pour obtenir le rayon. Divisez le volume par 4π, puis multipliez cette réponse par 3. Enfin, prenez la racine cubique de cette réponse.
-
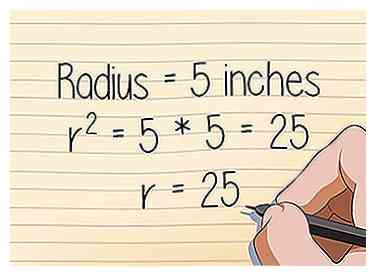 3 Carrez le rayon en le multipliant par lui-même. Vous pouvez soit le faire en multipliant manuellement (52 = 5 * 5 = 25) ou en utilisant la fonction "carrée" de votre calculatrice (parfois appelée "x2").
3 Carrez le rayon en le multipliant par lui-même. Vous pouvez soit le faire en multipliant manuellement (52 = 5 * 5 = 25) ou en utilisant la fonction "carrée" de votre calculatrice (parfois appelée "x2"). -
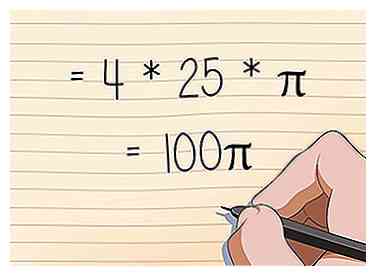 4 Multipliez ce résultat par 4. Bien que vous puissiez multiplier 4 ou pi en premier, il est généralement plus facile de commencer avec 4 car il n'y a pas encore de décimales à multiplier.
4 Multipliez ce résultat par 4. Bien que vous puissiez multiplier 4 ou pi en premier, il est généralement plus facile de commencer avec 4 car il n'y a pas encore de décimales à multiplier. - Si notre rayon est 5, comme ci-dessus, il vous restera 4 * 25 * π, ou 100π.
-
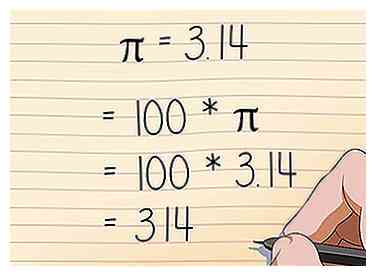 5 Multipliez les résultats par pi (π). Si votre problème dit "valeur exacte", écrivez le symbole π après votre numéro et appelez-le terminé. Sinon, utilisez l'approximation π = 3.14 ou le bouton π de votre calculatrice.
5 Multipliez les résultats par pi (π). Si votre problème dit "valeur exacte", écrivez le symbole π après votre numéro et appelez-le terminé. Sinon, utilisez l'approximation π = 3.14 ou le bouton π de votre calculatrice. - 100 * π = 100 * 3.14
- 100π = 314
-
 6 N'oubliez pas d'ajouter vos unités à la réponse finale. La surface de votre sphère est-elle de 314 pouces ou 314 milles? Les unités doivent être écrites comme "unités2, "car cela dénote une zone, également appelée" unités carrées "
6 N'oubliez pas d'ajouter vos unités à la réponse finale. La surface de votre sphère est-elle de 314 pouces ou 314 milles? Les unités doivent être écrites comme "unités2, "car cela dénote une zone, également appelée" unités carrées " - La réponse complète à la sphère dans les images est la suivante: Surface = 314 unités2.
- Les unités que vous utilisez sont toujours les mêmes que ceux utilisés pour mesurer le rayon. Si le rayon est en mètres, la réponse sera en mètres.
- Astuce avancée: Nous carissons les unités car la surface mesure le nombre de carrés que nous pourrions placer sur la surface de la sphère. Disons que nous mesurons le problème de la pratique en pouces. Cela signifie que sur une sphère où r = 5, nous pourrions ajuster 314 carrés à la surface de la sphère si les côtés de chaque carré ont 1 pouce de long.
-
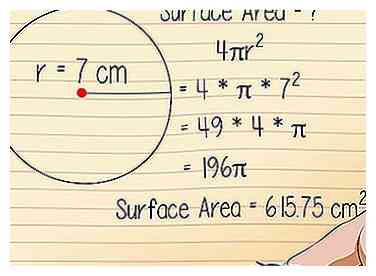 7 Pratique avec un exemple. Si le rayon d'une sphère est de 7 centimètres, quelle est la surface de cette sphère?
7 Pratique avec un exemple. Si le rayon d'une sphère est de 7 centimètres, quelle est la surface de cette sphère? - 4πr2
- r = 7
- 4 * π * 72
- 49 * 4 * π
- 196π
- Répondre: Surface: 615,75 centimètres2, ou 615,75 centimètres carrés.
-
 8 Comprendre la surface La surface d'une sphère est la zone qui recouvre l'extérieur de la sphère - pensez-y comme le caoutchouc qui recouvre un ballon ou la surface de la terre. Comme il est incurvé, il est beaucoup plus difficile de mesurer la surface d'une sphère qu'une boîte. Nous avons donc besoin d'une équation pour déterminer la surface.
8 Comprendre la surface La surface d'une sphère est la zone qui recouvre l'extérieur de la sphère - pensez-y comme le caoutchouc qui recouvre un ballon ou la surface de la terre. Comme il est incurvé, il est beaucoup plus difficile de mesurer la surface d'une sphère qu'une boîte. Nous avons donc besoin d'une équation pour déterminer la surface. - Faire tourner un cercle autour de son axe (le point central) produira une sphère. Pensez à faire tourner une pièce sur la table et à voir comment elle semble former une sphère. Bien que cela ne soit pas expliqué ici, c'est de là que vient notre équation.
- Astuce avancée: Les sphères ont une surface par volume inférieure à toute autre forme, ce qui signifie qu’elle peut contenir plus de choses dans une zone plus petite que toute autre forme.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Connaître les parties de l'équation, Surface Surface = 4πr2. Cette formule presque ancienne reste la manière la plus simple de déterminer la surface d'une sphère. En utilisant presque n'importe quelle calculatrice, vous pouvez brancher le rayon pour obtenir la surface de votre sphère.
1 Connaître les parties de l'équation, Surface Surface = 4πr2. Cette formule presque ancienne reste la manière la plus simple de déterminer la surface d'une sphère. En utilisant presque n'importe quelle calculatrice, vous pouvez brancher le rayon pour obtenir la surface de votre sphère.  2 Trouve le rayon de la sphère. Parfois, votre problème vous fournira le rayon, et d'autres fois vous devrez le trouver vous-même. Si on vous donne le diamètre d'un cercle, divisez simplement le diamètre par 2 pour obtenir le rayon. Par exemple, une sphère de diamètre 10 pouces a un rayon de 5 pouces.
2 Trouve le rayon de la sphère. Parfois, votre problème vous fournira le rayon, et d'autres fois vous devrez le trouver vous-même. Si on vous donne le diamètre d'un cercle, divisez simplement le diamètre par 2 pour obtenir le rayon. Par exemple, une sphère de diamètre 10 pouces a un rayon de 5 pouces. 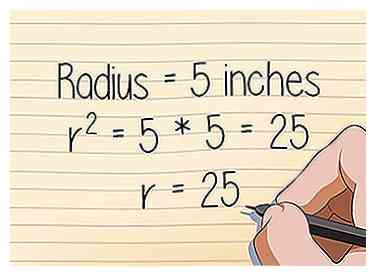 3 Carrez le rayon en le multipliant par lui-même. Vous pouvez soit le faire en multipliant manuellement (52 = 5 * 5 = 25) ou en utilisant la fonction "carrée" de votre calculatrice (parfois appelée "x2").
3 Carrez le rayon en le multipliant par lui-même. Vous pouvez soit le faire en multipliant manuellement (52 = 5 * 5 = 25) ou en utilisant la fonction "carrée" de votre calculatrice (parfois appelée "x2"). 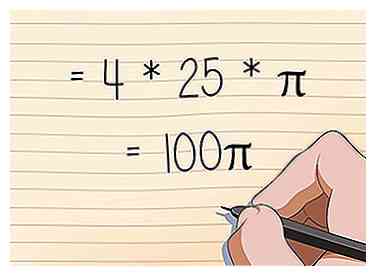 4 Multipliez ce résultat par 4. Bien que vous puissiez multiplier 4 ou pi en premier, il est généralement plus facile de commencer avec 4 car il n'y a pas encore de décimales à multiplier.
4 Multipliez ce résultat par 4. Bien que vous puissiez multiplier 4 ou pi en premier, il est généralement plus facile de commencer avec 4 car il n'y a pas encore de décimales à multiplier. 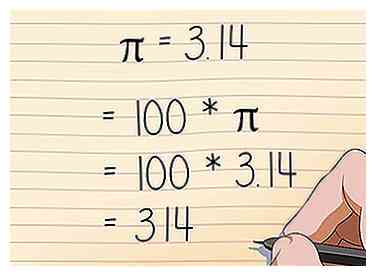 5 Multipliez les résultats par pi (π). Si votre problème dit "valeur exacte", écrivez le symbole π après votre numéro et appelez-le terminé. Sinon, utilisez l'approximation π = 3.14 ou le bouton π de votre calculatrice.
5 Multipliez les résultats par pi (π). Si votre problème dit "valeur exacte", écrivez le symbole π après votre numéro et appelez-le terminé. Sinon, utilisez l'approximation π = 3.14 ou le bouton π de votre calculatrice.  6 N'oubliez pas d'ajouter vos unités à la réponse finale. La surface de votre sphère est-elle de 314 pouces ou 314 milles? Les unités doivent être écrites comme "unités2, "car cela dénote une zone, également appelée" unités carrées "
6 N'oubliez pas d'ajouter vos unités à la réponse finale. La surface de votre sphère est-elle de 314 pouces ou 314 milles? Les unités doivent être écrites comme "unités2, "car cela dénote une zone, également appelée" unités carrées "  7 Pratique avec un exemple. Si le rayon d'une sphère est de 7 centimètres, quelle est la surface de cette sphère?
7 Pratique avec un exemple. Si le rayon d'une sphère est de 7 centimètres, quelle est la surface de cette sphère?  8 Comprendre la surface La surface d'une sphère est la zone qui recouvre l'extérieur de la sphère - pensez-y comme le caoutchouc qui recouvre un ballon ou la surface de la terre. Comme il est incurvé, il est beaucoup plus difficile de mesurer la surface d'une sphère qu'une boîte. Nous avons donc besoin d'une équation pour déterminer la surface.
8 Comprendre la surface La surface d'une sphère est la zone qui recouvre l'extérieur de la sphère - pensez-y comme le caoutchouc qui recouvre un ballon ou la surface de la terre. Comme il est incurvé, il est beaucoup plus difficile de mesurer la surface d'une sphère qu'une boîte. Nous avons donc besoin d'une équation pour déterminer la surface.