La surface d'une forme est la somme de la surface de toutes ses faces. Pour trouver l'aire d'un cylindre, vous devez trouver l'aire de ses bases et l'ajouter à la surface de son mur extérieur. La formule pour trouver l'aire d'un cylindre est A = 2πr2 + 2πrh.
Première partie de trois:
Calcul de la surface des cercles (2 x (π x r2))
-
 1 Visualisez le haut et le bas d'un cylindre. Une canette de soupe a la forme d'un cylindre. Si vous y réfléchissez, la boîte a un sommet et un fond identiques. Ces deux extrémités ont la forme d'un cercle. La première étape pour trouver la surface de votre cylindre sera de trouver la surface de ces extrémités circulaires.[1]
1 Visualisez le haut et le bas d'un cylindre. Une canette de soupe a la forme d'un cylindre. Si vous y réfléchissez, la boîte a un sommet et un fond identiques. Ces deux extrémités ont la forme d'un cercle. La première étape pour trouver la surface de votre cylindre sera de trouver la surface de ces extrémités circulaires.[1] -
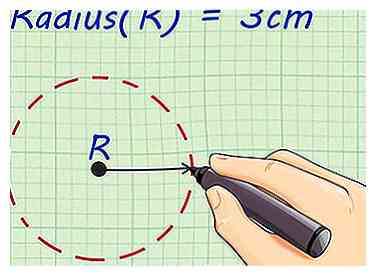 2 Trouvez le rayon de votre cylindre. Le rayon est la distance entre le centre d'un cercle et le bord extérieur du cercle. Le rayon est abrégé «r». Le rayon de votre cylindre est le même que celui des cercles supérieur et inférieur. Dans cet exemple, le rayon de la base est de 3 centimètres (1,2 pouce).[2]
2 Trouvez le rayon de votre cylindre. Le rayon est la distance entre le centre d'un cercle et le bord extérieur du cercle. Le rayon est abrégé «r». Le rayon de votre cylindre est le même que celui des cercles supérieur et inférieur. Dans cet exemple, le rayon de la base est de 3 centimètres (1,2 pouce).[2] - Si vous résolvez un problème de mot, le rayon peut être donné. Le diamètre peut également être donné, qui est la distance d'un côté du cercle à l'autre, en passant par le point central. Le rayon est exactement la moitié du diamètre.
- Vous pouvez mesurer le rayon avec une règle si vous recherchez la surface d'un cylindre réel.
-
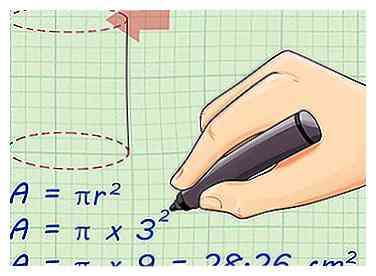 3 Calculez la surface du cercle supérieur. La surface d'un cercle est égale au nombre pi (~ 3,14) fois le rayon du cercle au carré. L'équation est écrite comme π x r2. C'est la même chose que de dire π x r x r.
3 Calculez la surface du cercle supérieur. La surface d'un cercle est égale au nombre pi (~ 3,14) fois le rayon du cercle au carré. L'équation est écrite comme π x r2. C'est la même chose que de dire π x r x r. - Pour trouver l'aire de la base, branchez simplement le rayon, 3 centimètres, dans l'équation pour trouver l'aire d'un cercle: A = πr2. Voici comment vous le faites:[3]
- A = πr2
- A = π x 32
- A = π x 9 = 28,26 cm2
-
 4 Recommencez pour le cercle de l'autre côté. Maintenant que vous avez résolu pour la zone d'une base, vous devez prendre en compte la zone de la deuxième base. Vous pouvez suivre les mêmes étapes que pour la première base ou reconnaître que les bases sont identiques. Vous pouvez sauter l'équation de la zone une deuxième fois pour la deuxième base si vous comprenez cela.[4]
4 Recommencez pour le cercle de l'autre côté. Maintenant que vous avez résolu pour la zone d'une base, vous devez prendre en compte la zone de la deuxième base. Vous pouvez suivre les mêmes étapes que pour la première base ou reconnaître que les bases sont identiques. Vous pouvez sauter l'équation de la zone une deuxième fois pour la deuxième base si vous comprenez cela.[4]
Deuxième partie de trois:
Calcul de l'aire de la surface du bord (2π x r x h)
-
 1 Visualisez le bord extérieur d'un cylindre. Lorsque vous visualisez une boîte de conserve cylindrique, vous devriez voir une base supérieure et une base inférieure. Les bases sont reliées entre elles par un «mur» de canette. Le rayon du mur est identique au rayon de la base, mais contrairement à la base, le mur a de la hauteur.[5]
1 Visualisez le bord extérieur d'un cylindre. Lorsque vous visualisez une boîte de conserve cylindrique, vous devriez voir une base supérieure et une base inférieure. Les bases sont reliées entre elles par un «mur» de canette. Le rayon du mur est identique au rayon de la base, mais contrairement à la base, le mur a de la hauteur.[5] -
 2 Trouvez la circonférence de l'un des cercles. Vous devrez trouver la circonférence pour trouver la surface du bord extérieur (également appelée surface latérale). Pour obtenir la circonférence, multipliez simplement le rayon par 2π. Ainsi, la circonférence peut être trouvée en multipliant 3 centimètres (1,2 pouce) par 2π. 3 centimètres (1,2 pouce) x 2π = 18,84 centimètres (7,4 pouces).[6]
2 Trouvez la circonférence de l'un des cercles. Vous devrez trouver la circonférence pour trouver la surface du bord extérieur (également appelée surface latérale). Pour obtenir la circonférence, multipliez simplement le rayon par 2π. Ainsi, la circonférence peut être trouvée en multipliant 3 centimètres (1,2 pouce) par 2π. 3 centimètres (1,2 pouce) x 2π = 18,84 centimètres (7,4 pouces).[6] -
 3 Multipliez la circonférence du cercle par la hauteur du cylindre. Cela vous donnera la surface extérieure du bord. Multipliez la circonférence, 18,84 centimètres (7,4 pouces), par la hauteur, 5 centimètres (2,0 pouces). 18,84 centimètres (7,4 pouces) x 5 centimètres (2,0 pouces) = 94,2 cm2.[7]
3 Multipliez la circonférence du cercle par la hauteur du cylindre. Cela vous donnera la surface extérieure du bord. Multipliez la circonférence, 18,84 centimètres (7,4 pouces), par la hauteur, 5 centimètres (2,0 pouces). 18,84 centimètres (7,4 pouces) x 5 centimètres (2,0 pouces) = 94,2 cm2.[7]
Troisième partie de trois:
Le mettre ensemble ((2) x (π x r2)) + (2π x r x h)
-
 1 Visualisez le cylindre entier. Tout d'abord, vous avez visualisé comment la base supérieure et inférieure et résolu pour la zone contenue sur ces surfaces. Ensuite, vous avez pensé au mur qui s'étend entre ces bases et résolu pour cet espace. Cette fois, pensez à la boîte dans son ensemble et vous résolvez pour toute la surface.[8]
1 Visualisez le cylindre entier. Tout d'abord, vous avez visualisé comment la base supérieure et inférieure et résolu pour la zone contenue sur ces surfaces. Ensuite, vous avez pensé au mur qui s'étend entre ces bases et résolu pour cet espace. Cette fois, pensez à la boîte dans son ensemble et vous résolvez pour toute la surface.[8] -
 2 Doublez l'aire d'une base. Multipliez simplement le résultat précédent, 28,26 cm2, par 2 pour obtenir l'aire des deux bases. 28,26 x 2 = 56,52 cm2. Cela vous donne la zone des deux bases.[9]
2 Doublez l'aire d'une base. Multipliez simplement le résultat précédent, 28,26 cm2, par 2 pour obtenir l'aire des deux bases. 28,26 x 2 = 56,52 cm2. Cela vous donne la zone des deux bases.[9] -
 3 Ajoutez la zone du mur et la zone de base. Une fois que vous avez ajouté l'aire des deux bases et la surface extérieure, vous avez trouvé la surface du cylindre. Tout ce que vous avez à faire est d'ajouter 56,52 cm2, la superficie des deux bases et la surface extérieure, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150,72 cm2. La surface avec un cylindre d'une hauteur de 5 centimètres (2,0 pouces) et une base circulaire avec un rayon de 3 centimètres (1,2 pouce) est de 150,72 cm2.[10]
3 Ajoutez la zone du mur et la zone de base. Une fois que vous avez ajouté l'aire des deux bases et la surface extérieure, vous avez trouvé la surface du cylindre. Tout ce que vous avez à faire est d'ajouter 56,52 cm2, la superficie des deux bases et la surface extérieure, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150,72 cm2. La surface avec un cylindre d'une hauteur de 5 centimètres (2,0 pouces) et une base circulaire avec un rayon de 3 centimètres (1,2 pouce) est de 150,72 cm2.[10]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Visualisez le haut et le bas d'un cylindre. Une canette de soupe a la forme d'un cylindre. Si vous y réfléchissez, la boîte a un sommet et un fond identiques. Ces deux extrémités ont la forme d'un cercle. La première étape pour trouver la surface de votre cylindre sera de trouver la surface de ces extrémités circulaires.[1]
1 Visualisez le haut et le bas d'un cylindre. Une canette de soupe a la forme d'un cylindre. Si vous y réfléchissez, la boîte a un sommet et un fond identiques. Ces deux extrémités ont la forme d'un cercle. La première étape pour trouver la surface de votre cylindre sera de trouver la surface de ces extrémités circulaires.[1]  2 Trouvez le rayon de votre cylindre. Le rayon est la distance entre le centre d'un cercle et le bord extérieur du cercle. Le rayon est abrégé «r». Le rayon de votre cylindre est le même que celui des cercles supérieur et inférieur. Dans cet exemple, le rayon de la base est de 3 centimètres (1,2 pouce).[2]
2 Trouvez le rayon de votre cylindre. Le rayon est la distance entre le centre d'un cercle et le bord extérieur du cercle. Le rayon est abrégé «r». Le rayon de votre cylindre est le même que celui des cercles supérieur et inférieur. Dans cet exemple, le rayon de la base est de 3 centimètres (1,2 pouce).[2]  3 Calculez la surface du cercle supérieur. La surface d'un cercle est égale au nombre pi (~ 3,14) fois le rayon du cercle au carré. L'équation est écrite comme π x r2. C'est la même chose que de dire π x r x r.
3 Calculez la surface du cercle supérieur. La surface d'un cercle est égale au nombre pi (~ 3,14) fois le rayon du cercle au carré. L'équation est écrite comme π x r2. C'est la même chose que de dire π x r x r.  4 Recommencez pour le cercle de l'autre côté. Maintenant que vous avez résolu pour la zone d'une base, vous devez prendre en compte la zone de la deuxième base. Vous pouvez suivre les mêmes étapes que pour la première base ou reconnaître que les bases sont identiques. Vous pouvez sauter l'équation de la zone une deuxième fois pour la deuxième base si vous comprenez cela.[4]
4 Recommencez pour le cercle de l'autre côté. Maintenant que vous avez résolu pour la zone d'une base, vous devez prendre en compte la zone de la deuxième base. Vous pouvez suivre les mêmes étapes que pour la première base ou reconnaître que les bases sont identiques. Vous pouvez sauter l'équation de la zone une deuxième fois pour la deuxième base si vous comprenez cela.[4]  1 Visualisez le bord extérieur d'un cylindre. Lorsque vous visualisez une boîte de conserve cylindrique, vous devriez voir une base supérieure et une base inférieure. Les bases sont reliées entre elles par un «mur» de canette. Le rayon du mur est identique au rayon de la base, mais contrairement à la base, le mur a de la hauteur.[5]
1 Visualisez le bord extérieur d'un cylindre. Lorsque vous visualisez une boîte de conserve cylindrique, vous devriez voir une base supérieure et une base inférieure. Les bases sont reliées entre elles par un «mur» de canette. Le rayon du mur est identique au rayon de la base, mais contrairement à la base, le mur a de la hauteur.[5]  2 Trouvez la circonférence de l'un des cercles. Vous devrez trouver la circonférence pour trouver la surface du bord extérieur (également appelée surface latérale). Pour obtenir la circonférence, multipliez simplement le rayon par 2π. Ainsi, la circonférence peut être trouvée en multipliant 3 centimètres (1,2 pouce) par 2π. 3 centimètres (1,2 pouce) x 2π = 18,84 centimètres (7,4 pouces).[6]
2 Trouvez la circonférence de l'un des cercles. Vous devrez trouver la circonférence pour trouver la surface du bord extérieur (également appelée surface latérale). Pour obtenir la circonférence, multipliez simplement le rayon par 2π. Ainsi, la circonférence peut être trouvée en multipliant 3 centimètres (1,2 pouce) par 2π. 3 centimètres (1,2 pouce) x 2π = 18,84 centimètres (7,4 pouces).[6]  3 Multipliez la circonférence du cercle par la hauteur du cylindre. Cela vous donnera la surface extérieure du bord. Multipliez la circonférence, 18,84 centimètres (7,4 pouces), par la hauteur, 5 centimètres (2,0 pouces). 18,84 centimètres (7,4 pouces) x 5 centimètres (2,0 pouces) = 94,2 cm2.[7]
3 Multipliez la circonférence du cercle par la hauteur du cylindre. Cela vous donnera la surface extérieure du bord. Multipliez la circonférence, 18,84 centimètres (7,4 pouces), par la hauteur, 5 centimètres (2,0 pouces). 18,84 centimètres (7,4 pouces) x 5 centimètres (2,0 pouces) = 94,2 cm2.[7]  1 Visualisez le cylindre entier. Tout d'abord, vous avez visualisé comment la base supérieure et inférieure et résolu pour la zone contenue sur ces surfaces. Ensuite, vous avez pensé au mur qui s'étend entre ces bases et résolu pour cet espace. Cette fois, pensez à la boîte dans son ensemble et vous résolvez pour toute la surface.[8]
1 Visualisez le cylindre entier. Tout d'abord, vous avez visualisé comment la base supérieure et inférieure et résolu pour la zone contenue sur ces surfaces. Ensuite, vous avez pensé au mur qui s'étend entre ces bases et résolu pour cet espace. Cette fois, pensez à la boîte dans son ensemble et vous résolvez pour toute la surface.[8]  2 Doublez l'aire d'une base. Multipliez simplement le résultat précédent, 28,26 cm2, par 2 pour obtenir l'aire des deux bases. 28,26 x 2 = 56,52 cm2. Cela vous donne la zone des deux bases.[9]
2 Doublez l'aire d'une base. Multipliez simplement le résultat précédent, 28,26 cm2, par 2 pour obtenir l'aire des deux bases. 28,26 x 2 = 56,52 cm2. Cela vous donne la zone des deux bases.[9]  3 Ajoutez la zone du mur et la zone de base. Une fois que vous avez ajouté l'aire des deux bases et la surface extérieure, vous avez trouvé la surface du cylindre. Tout ce que vous avez à faire est d'ajouter 56,52 cm2, la superficie des deux bases et la surface extérieure, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150,72 cm2. La surface avec un cylindre d'une hauteur de 5 centimètres (2,0 pouces) et une base circulaire avec un rayon de 3 centimètres (1,2 pouce) est de 150,72 cm2.[10]
3 Ajoutez la zone du mur et la zone de base. Une fois que vous avez ajouté l'aire des deux bases et la surface extérieure, vous avez trouvé la surface du cylindre. Tout ce que vous avez à faire est d'ajouter 56,52 cm2, la superficie des deux bases et la surface extérieure, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150,72 cm2. La surface avec un cylindre d'une hauteur de 5 centimètres (2,0 pouces) et une base circulaire avec un rayon de 3 centimètres (1,2 pouce) est de 150,72 cm2.[10]