L'apprentissage du cercle d'unités vous aidera non seulement en trigonométrie et en géométrie, mais également dans les futurs cours de calcul. Cela peut sembler beaucoup à mémoriser, mais une fois que vous avez compris comment cela fonctionne, vous pouvez commencer avec quelques chiffres et déterminer rapidement le reste.
Première partie de deux:
Mémorisation des radians
-
 1 Dessine deux lignes perpendiculaires. Placez une règle sur une grande feuille de papier. Tracez une ligne verticale et une ligne horizontale. Celles-ci doivent se croiser près du centre de la page. Voici les X et y les axes d'un graphique.
1 Dessine deux lignes perpendiculaires. Placez une règle sur une grande feuille de papier. Tracez une ligne verticale et une ligne horizontale. Celles-ci doivent se croiser près du centre de la page. Voici les X et y les axes d'un graphique. -
 2 Tracez un cercle. À l'aide d'une boussole, dessinez un grand cercle avec son centre à l'intersection des deux lignes.
2 Tracez un cercle. À l'aide d'une boussole, dessinez un grand cercle avec son centre à l'intersection des deux lignes. -
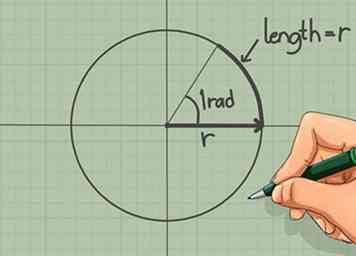 3 Comprendre les radians. Un radian est une mesure d'angle. Plus précisément, il est défini de telle sorte qu'une personne qui marche autour d'un cercle avec un rayon 1 unité balaie l'angle d'un radian après avoir marché pour 1 unité autour de la circonférence. Dans l'étape suivante, nous étiquetons les quatre points de coordonnées avec la valeur radian. Si vous mémorisez la formule pour associer la circonférence et le rayon, vous pouvez rapidement les supprimer, même si vous ne les avez pas mémorisées.
3 Comprendre les radians. Un radian est une mesure d'angle. Plus précisément, il est défini de telle sorte qu'une personne qui marche autour d'un cercle avec un rayon 1 unité balaie l'angle d'un radian après avoir marché pour 1 unité autour de la circonférence. Dans l'étape suivante, nous étiquetons les quatre points de coordonnées avec la valeur radian. Si vous mémorisez la formule pour associer la circonférence et le rayon, vous pouvez rapidement les supprimer, même si vous ne les avez pas mémorisées. - Les mesures radian du cercle d'unité supposent toujours que vous partez de la coordonnée (0, 1). Pour préciser le point auquel nous faisons référence, nous allons décrire le cercle comme une rose des vents:
-
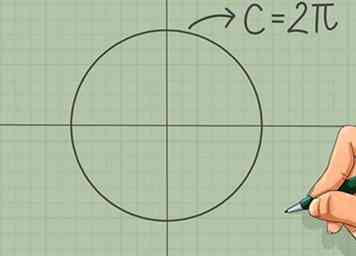 4 Rappelez-vous que la circonférence du cercle est 2π. La circonférence d'un cercle est égale à 2πr, où r est le rayon. Comme le cercle unitaire a un rayon de 1, on peut simplifier sa circonférence à 2π. Vous pouvez trouver la valeur radian de n'importe quel point de la circonférence, simplement en prenant 2π et en divisant par la fraction du cercle que vous avez couvert. C'est beaucoup plus facile que de mémoriser chaque valeur du cercle.
4 Rappelez-vous que la circonférence du cercle est 2π. La circonférence d'un cercle est égale à 2πr, où r est le rayon. Comme le cercle unitaire a un rayon de 1, on peut simplifier sa circonférence à 2π. Vous pouvez trouver la valeur radian de n'importe quel point de la circonférence, simplement en prenant 2π et en divisant par la fraction du cercle que vous avez couvert. C'est beaucoup plus facile que de mémoriser chaque valeur du cercle. -
 5 Étiquetez les quatre points sur les axes x et y. Tout ce qu'il faut, c'est diviser 2π en quarts:
5 Étiquetez les quatre points sur les axes x et y. Tout ce qu'il faut, c'est diviser 2π en quarts: - "Est" est le point de départ, donc vous avez couvert 0 radians.
- "Nord" = ¼ de la circonférence = 2π/4 = π/2 radians.
- "Ouest" = à mi-course = 2π/2 = π radians.
- Sud = trois quarts = 2π * ¾ = 3π/2 radians.
- Marcher sur toute la circonférence vous ramène à votre point de départ. Vous pouvez étiqueter ceci 2π ainsi que 0 pour représenter cela.
-
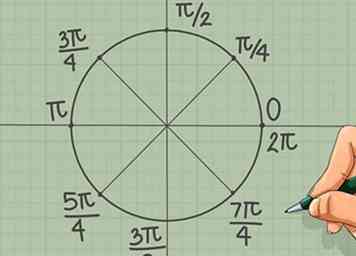 6 Divisez le cercle en huitièmes. Maintenant, tracez une ligne dans chaque quadrant en le coupant parfaitement en deux. Encore une fois, utilisez la division pour trouver la valeur en radians:
6 Divisez le cercle en huitièmes. Maintenant, tracez une ligne dans chaque quadrant en le coupant parfaitement en deux. Encore une fois, utilisez la division pour trouver la valeur en radians: - π/4
- 3π/4
- 5π/4
- 7π/4
- (π / 2, π, 3π / 2 et 2π sont déjà étiquetés.)
-
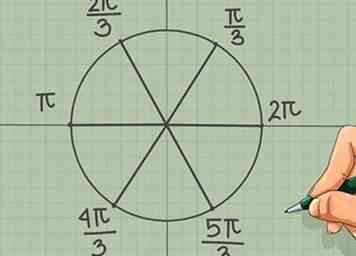 7 Diviser le cercle en six segments. Dessinez maintenant des lignes supplémentaires coupant le cercle en six segments. (Vous pouvez utiliser un rapporteur pour cela, en commençant par l’axe des x positif et en mesurant 60 degrés à chaque fois.) Vous pouvez utiliser la même approche ci-dessus pour vous rendre compte qu’un sixième de cercle couvre 2π/6 = π/3 radians. Utilisez cette option pour étiqueter les points suivants sur la circonférence (un dans chaque quadrant):
7 Diviser le cercle en six segments. Dessinez maintenant des lignes supplémentaires coupant le cercle en six segments. (Vous pouvez utiliser un rapporteur pour cela, en commençant par l’axe des x positif et en mesurant 60 degrés à chaque fois.) Vous pouvez utiliser la même approche ci-dessus pour vous rendre compte qu’un sixième de cercle couvre 2π/6 = π/3 radians. Utilisez cette option pour étiqueter les points suivants sur la circonférence (un dans chaque quadrant): - π/3
- 2π/3
- 4π/3
- 5π/3
- (π et 2π sont déjà étiquetés)
-
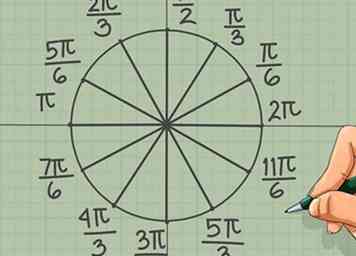 8 Dessine dans les douzièmes. Les derniers points marqués sur la plupart des cercles d'unités représentent des incréments d'un douzième de la circonférence. Seuls quatre d'entre eux n'ont pas encore été étiquetés:
8 Dessine dans les douzièmes. Les derniers points marqués sur la plupart des cercles d'unités représentent des incréments d'un douzième de la circonférence. Seuls quatre d'entre eux n'ont pas encore été étiquetés: - π/6
- 5π/6
- 7π/6
- 11π/6
Deuxième partie de deux:
Mémorisation des coordonnées X-Y (cosinus, sinus)
-
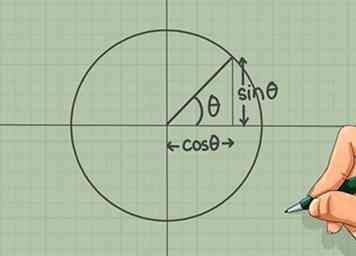 1 Comprenez le cosinus et le sinus. Le cercle unitaire est particulièrement utile pour la trigonométrie à angle droit. Chaque coordonnée x d'un point sur le cercle est égale au cosinus (θ) et chaque coordonnée y est égale à sinus (θ), où θ est la valeur de l'angle.
1 Comprenez le cosinus et le sinus. Le cercle unitaire est particulièrement utile pour la trigonométrie à angle droit. Chaque coordonnée x d'un point sur le cercle est égale au cosinus (θ) et chaque coordonnée y est égale à sinus (θ), où θ est la valeur de l'angle. - Si vous avez du mal à vous souvenir de cela, pensez (cos, sin) "parce que le sinistre passe en dernier".
- Vous pouvez dériver ceci en utilisant des triangles rectangles et la définition de ces fonctions - rappelez-vous "sohcahtoa"?
-
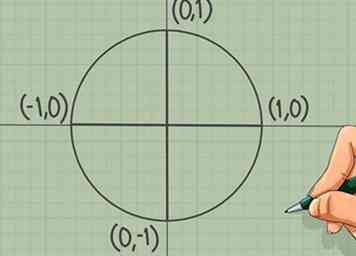 2 Écrivez les coordonnées sur quatre points du cercle. Un "cercle unitaire" est juste un cercle avec un rayon d'une unité de longueur. Utilisez ceci pour trouver le X et y coordonnées de quatre points sur le cercle, où il coupe un axe. (Nous appelons cela "Est", "Nord", etc. pour faciliter la lecture, mais ce ne sont pas des noms officiels.)
2 Écrivez les coordonnées sur quatre points du cercle. Un "cercle unitaire" est juste un cercle avec un rayon d'une unité de longueur. Utilisez ceci pour trouver le X et y coordonnées de quatre points sur le cercle, où il coupe un axe. (Nous appelons cela "Est", "Nord", etc. pour faciliter la lecture, mais ce ne sont pas des noms officiels.) - Les coordonnées du point "Est" sont (1, 0).
- Le point "Nord" est à (0, 1).
- Le point "Ouest" est à (-1, 0).
- Le point "Sud" est à (0, -1).
- Cela fonctionne comme un graphique normal. Vous devriez être capable de comprendre ces coordonnées vous-même, sans avoir à les mémoriser.
-
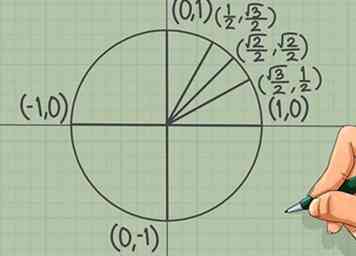 3 Mémorisez les coordonnées du premier quadrant. Le premier quadrant est le quart supérieur droit du cercle, où les deux X et y les valeurs sont positives. Ce sont les seules valeurs de coordonnées que vous devez mémoriser:
3 Mémorisez les coordonnées du premier quadrant. Le premier quadrant est le quart supérieur droit du cercle, où les deux X et y les valeurs sont positives. Ce sont les seules valeurs de coordonnées que vous devez mémoriser: - À π/6, les coordonnées sont ().
- À π/4, les coordonnées sont ().
- À π/3, les coordonnées sont ().
- Notez qu'il n'y a que trois numérateurs. Se déplacer dans une direction positive (de gauche à droite pour X valeurs, de bas en haut pour y valeurs), celles-ci devraient aller 1 → √2 → √3.
-
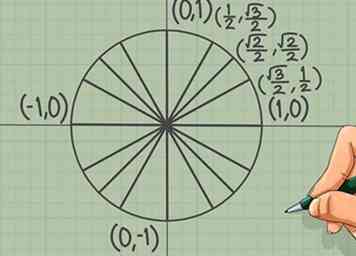 4 Tracez des lignes droites pour remplir d'autres coordonnées. Si vous pouvez tracer une ligne parfaitement verticale ou parfaitement horizontale entre deux points, ils ont la même valeur absolue que les coordonnées x et y. En d'autres termes, vous pouvez tracer une ligne à partir d'un point dans les premiers quadrants, écrire les mêmes coordonnées à l'endroit où vous vous trouvez et laisser de la place dans le signe (+ ou -).
4 Tracez des lignes droites pour remplir d'autres coordonnées. Si vous pouvez tracer une ligne parfaitement verticale ou parfaitement horizontale entre deux points, ils ont la même valeur absolue que les coordonnées x et y. En d'autres termes, vous pouvez tracer une ligne à partir d'un point dans les premiers quadrants, écrire les mêmes coordonnées à l'endroit où vous vous trouvez et laisser de la place dans le signe (+ ou -). - Par exemple, vous pouvez dessiner une ligne horizontale entre π/3 et 2π/3. Puisque les coordonnées au premier point sont (), les coordonnées au deuxième point sont (?), où "?" représente un signe + ou -.
- Voici un raccourci: vérifiez le dénominateur dans les radians. Tous les points se terminant par / 3 ont les mêmes coordonnées en valeur absolue, de même que tous les points se terminant par / 4 et tous les points se terminant par / 6.
-
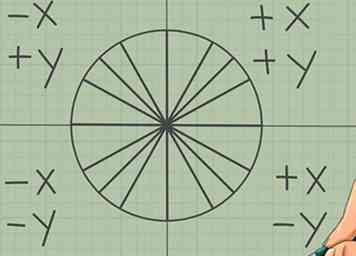 5 Utilisez la symétrie pour déterminer si elle est positive ou négative. Il y a plusieurs façons de mémoriser où placer les signes - sur votre cercle:
5 Utilisez la symétrie pour déterminer si elle est positive ou négative. Il y a plusieurs façons de mémoriser où placer les signes - sur votre cercle: - Pensez aux règles de base des graphes. Au dessus de X l'axe est positif, ci-dessous est négatif. À gauche du y l'axe est négatif, la droite est positive.
- Commencez à partir du quadrant 1 et tracez des lignes vers d'autres points. Si la ligne traverse le y axe, la valeur y change de signe. S'il traverse la X axe, le X signe de changement de valeur.
- Mémoriser "Tous les élèves prennent le calcul" (ASTC), se déplaçant dans le sens inverse des aiguilles d'une montre. Le quadrant 1 a UNEll valeurs positives, Q2 a positif Sine only, Q3 a positif Tangent uniquement et Q4 positif Cosine seulement.
- Quelle que soit la méthode choisie, les signes sont (+, +) pour le quadrant 1, (-, +) pour le quadrant 2, (-, -) pour le quadrant 3 et (+, -) pour le quadrant 4.
-
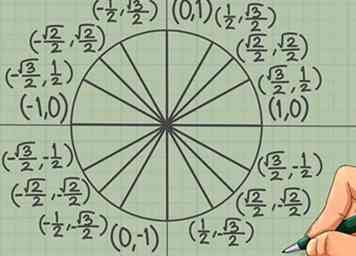 6 Vérifie ton travail. Voici la liste complète des valeurs de coordonnées à chaque point étiqueté de votre cercle (sans compter les quatre points sur les axes), dans le sens des aiguilles d'une montre. Rappelez-vous, vous devriez être capable de trouver toutes ces valeurs simplement en mémorisant le quadrant 1:
6 Vérifie ton travail. Voici la liste complète des valeurs de coordonnées à chaque point étiqueté de votre cercle (sans compter les quatre points sur les axes), dans le sens des aiguilles d'une montre. Rappelez-vous, vous devriez être capable de trouver toutes ces valeurs simplement en mémorisant le quadrant 1: - Quadrant 1: (); (); ().
- Quadrant 2: (); (); ()
- Quadrant 3: (); (); ()
- Quadrant 4: (); (); ()
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Dessine deux lignes perpendiculaires. Placez une règle sur une grande feuille de papier. Tracez une ligne verticale et une ligne horizontale. Celles-ci doivent se croiser près du centre de la page. Voici les X et y les axes d'un graphique.
1 Dessine deux lignes perpendiculaires. Placez une règle sur une grande feuille de papier. Tracez une ligne verticale et une ligne horizontale. Celles-ci doivent se croiser près du centre de la page. Voici les X et y les axes d'un graphique.  2 Tracez un cercle. À l'aide d'une boussole, dessinez un grand cercle avec son centre à l'intersection des deux lignes.
2 Tracez un cercle. À l'aide d'une boussole, dessinez un grand cercle avec son centre à l'intersection des deux lignes.  3 Comprendre les radians. Un radian est une mesure d'angle. Plus précisément, il est défini de telle sorte qu'une personne qui marche autour d'un cercle avec un rayon 1 unité balaie l'angle d'un radian après avoir marché pour 1 unité autour de la circonférence. Dans l'étape suivante, nous étiquetons les quatre points de coordonnées avec la valeur radian. Si vous mémorisez la formule pour associer la circonférence et le rayon, vous pouvez rapidement les supprimer, même si vous ne les avez pas mémorisées.
3 Comprendre les radians. Un radian est une mesure d'angle. Plus précisément, il est défini de telle sorte qu'une personne qui marche autour d'un cercle avec un rayon 1 unité balaie l'angle d'un radian après avoir marché pour 1 unité autour de la circonférence. Dans l'étape suivante, nous étiquetons les quatre points de coordonnées avec la valeur radian. Si vous mémorisez la formule pour associer la circonférence et le rayon, vous pouvez rapidement les supprimer, même si vous ne les avez pas mémorisées.  4 Rappelez-vous que la circonférence du cercle est 2π. La circonférence d'un cercle est égale à 2πr, où r est le rayon. Comme le cercle unitaire a un rayon de 1, on peut simplifier sa circonférence à 2π. Vous pouvez trouver la valeur radian de n'importe quel point de la circonférence, simplement en prenant 2π et en divisant par la fraction du cercle que vous avez couvert. C'est beaucoup plus facile que de mémoriser chaque valeur du cercle.
4 Rappelez-vous que la circonférence du cercle est 2π. La circonférence d'un cercle est égale à 2πr, où r est le rayon. Comme le cercle unitaire a un rayon de 1, on peut simplifier sa circonférence à 2π. Vous pouvez trouver la valeur radian de n'importe quel point de la circonférence, simplement en prenant 2π et en divisant par la fraction du cercle que vous avez couvert. C'est beaucoup plus facile que de mémoriser chaque valeur du cercle.  5 Étiquetez les quatre points sur les axes x et y. Tout ce qu'il faut, c'est diviser 2π en quarts:
5 Étiquetez les quatre points sur les axes x et y. Tout ce qu'il faut, c'est diviser 2π en quarts:  6 Divisez le cercle en huitièmes. Maintenant, tracez une ligne dans chaque quadrant en le coupant parfaitement en deux. Encore une fois, utilisez la division pour trouver la valeur en radians:
6 Divisez le cercle en huitièmes. Maintenant, tracez une ligne dans chaque quadrant en le coupant parfaitement en deux. Encore une fois, utilisez la division pour trouver la valeur en radians:  7 Diviser le cercle en six segments. Dessinez maintenant des lignes supplémentaires coupant le cercle en six segments. (Vous pouvez utiliser un rapporteur pour cela, en commençant par l’axe des x positif et en mesurant 60 degrés à chaque fois.) Vous pouvez utiliser la même approche ci-dessus pour vous rendre compte qu’un sixième de cercle couvre 2π/6 = π/3 radians. Utilisez cette option pour étiqueter les points suivants sur la circonférence (un dans chaque quadrant):
7 Diviser le cercle en six segments. Dessinez maintenant des lignes supplémentaires coupant le cercle en six segments. (Vous pouvez utiliser un rapporteur pour cela, en commençant par l’axe des x positif et en mesurant 60 degrés à chaque fois.) Vous pouvez utiliser la même approche ci-dessus pour vous rendre compte qu’un sixième de cercle couvre 2π/6 = π/3 radians. Utilisez cette option pour étiqueter les points suivants sur la circonférence (un dans chaque quadrant):  8 Dessine dans les douzièmes. Les derniers points marqués sur la plupart des cercles d'unités représentent des incréments d'un douzième de la circonférence. Seuls quatre d'entre eux n'ont pas encore été étiquetés:
8 Dessine dans les douzièmes. Les derniers points marqués sur la plupart des cercles d'unités représentent des incréments d'un douzième de la circonférence. Seuls quatre d'entre eux n'ont pas encore été étiquetés:  1 Comprenez le cosinus et le sinus. Le cercle unitaire est particulièrement utile pour la trigonométrie à angle droit. Chaque coordonnée x d'un point sur le cercle est égale au cosinus (θ) et chaque coordonnée y est égale à sinus (θ), où θ est la valeur de l'angle.
1 Comprenez le cosinus et le sinus. Le cercle unitaire est particulièrement utile pour la trigonométrie à angle droit. Chaque coordonnée x d'un point sur le cercle est égale au cosinus (θ) et chaque coordonnée y est égale à sinus (θ), où θ est la valeur de l'angle.  2 Écrivez les coordonnées sur quatre points du cercle. Un "cercle unitaire" est juste un cercle avec un rayon d'une unité de longueur. Utilisez ceci pour trouver le X et y coordonnées de quatre points sur le cercle, où il coupe un axe. (Nous appelons cela "Est", "Nord", etc. pour faciliter la lecture, mais ce ne sont pas des noms officiels.)
2 Écrivez les coordonnées sur quatre points du cercle. Un "cercle unitaire" est juste un cercle avec un rayon d'une unité de longueur. Utilisez ceci pour trouver le X et y coordonnées de quatre points sur le cercle, où il coupe un axe. (Nous appelons cela "Est", "Nord", etc. pour faciliter la lecture, mais ce ne sont pas des noms officiels.)  3 Mémorisez les coordonnées du premier quadrant. Le premier quadrant est le quart supérieur droit du cercle, où les deux X et y les valeurs sont positives. Ce sont les seules valeurs de coordonnées que vous devez mémoriser:
3 Mémorisez les coordonnées du premier quadrant. Le premier quadrant est le quart supérieur droit du cercle, où les deux X et y les valeurs sont positives. Ce sont les seules valeurs de coordonnées que vous devez mémoriser:  4 Tracez des lignes droites pour remplir d'autres coordonnées. Si vous pouvez tracer une ligne parfaitement verticale ou parfaitement horizontale entre deux points, ils ont la même valeur absolue que les coordonnées x et y. En d'autres termes, vous pouvez tracer une ligne à partir d'un point dans les premiers quadrants, écrire les mêmes coordonnées à l'endroit où vous vous trouvez et laisser de la place dans le signe (+ ou -).
4 Tracez des lignes droites pour remplir d'autres coordonnées. Si vous pouvez tracer une ligne parfaitement verticale ou parfaitement horizontale entre deux points, ils ont la même valeur absolue que les coordonnées x et y. En d'autres termes, vous pouvez tracer une ligne à partir d'un point dans les premiers quadrants, écrire les mêmes coordonnées à l'endroit où vous vous trouvez et laisser de la place dans le signe (+ ou -).  5 Utilisez la symétrie pour déterminer si elle est positive ou négative. Il y a plusieurs façons de mémoriser où placer les signes - sur votre cercle:
5 Utilisez la symétrie pour déterminer si elle est positive ou négative. Il y a plusieurs façons de mémoriser où placer les signes - sur votre cercle:  6 Vérifie ton travail. Voici la liste complète des valeurs de coordonnées à chaque point étiqueté de votre cercle (sans compter les quatre points sur les axes), dans le sens des aiguilles d'une montre. Rappelez-vous, vous devriez être capable de trouver toutes ces valeurs simplement en mémorisant le quadrant 1:
6 Vérifie ton travail. Voici la liste complète des valeurs de coordonnées à chaque point étiqueté de votre cercle (sans compter les quatre points sur les axes), dans le sens des aiguilles d'une montre. Rappelez-vous, vous devriez être capable de trouver toutes ces valeurs simplement en mémorisant le quadrant 1: